《2025年名校课堂七年级数学3上册人教版广东专版》

5. 【例3】写出下列各数的倒数：
$5$，$-5$，$\frac{1}{3}$，$-\frac{1}{3}$，$\frac{2}{3}$，$-\frac{2}{3}$。

答案： 5.解:5的倒数是$\frac{1}{5}$;-5的倒数是$-\frac{1}{5}$;$\frac{1}{3}$的倒数是3;$-\frac{1}{3}$的倒数是-3;$\frac{2}{3}$的倒数是$\frac{3}{2}$;$-\frac{2}{3}$的倒数是$-\frac{3}{2}$.

6. 写出下列各数的倒数：
$-15$，$-\frac{5}{9}$，$-0.25$，$0.17$，$4\frac{1}{4}$，$-5\frac{2}{5}$。

答案： 6.解:-15的倒数是$-\frac{1}{15}$;$-\frac{5}{9}$的倒数是$-\frac{9}{5}$;-0.25的倒数是-4;0.17的倒数是$\frac{100}{17}$;$4\frac{1}{4}$的倒数是$\frac{4}{17}$;$-5\frac{2}{5}$的倒数是$-\frac{5}{27}$.

7. 【例4】(人教7上P40例2)用正负数表示气温的变化量，上升为正，下降为负。登山队攀登一座山峰，每登高1km气温的变化量为$-6^{\circ}C$，攀登3km后，气温有什么变化？

答案： 7.解:(-6)×3=-18.
答:登高3 km后,气温下降18℃.

8. (人教7上P40练习T2)商店降价销售某种商品，每件降5元，售出60件，与按原价销售同样数量的商品相比，销售额有什么变化？

答案： 8.解:-5×60=-300.
答:销售额减少了300元.

9. (2024·陕西)$-3$的倒数是(A)

A.$-\frac{1}{3}$
B.$\frac{1}{3}$
C.$-3$
D.3

答案： 9.A

10. 计算：
(1)$(-3)×(-5) =$15；
(2)$(-7)×8 =$-56；
(3)$0×(-9) =$0；
(4)$(-4)×0.25 =$-1。

答案： 10.
(1)15
(2)-56
(3)0
(4)-1

11. 计算：
(1)$\frac{5}{6}×(-12)$；
(2)$100×(-0.001)$；
(3)$(-3\frac{1}{2})×(-4)$；
(4)$(-4\frac{2}{3})×0.25$。

答案： 11.解:
(1)原式=-10.
(2)原式=-0.1.
(3)原式$=\frac{7}{2}×4=14$.
(4)原式$=-\frac{14}{3}×\frac{1}{4}=-\frac{7}{6}$.

12. 下列说法中，正确的有①②③。(填序号)
①一个数同1相乘，仍得这个数；
②一个数同$-1$相乘，得这个数的相反数；
③一个数同0相乘，仍得0。

答案： 12.①②③

13. 某商店每天亏损20元，则一周(按7天计)的利润为-140元。

答案： 13.-140

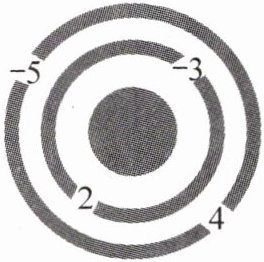
14. 新考向 情境素材 一座两道环路的数字迷宫如图所示，外环两个路口的数字分别为$-5$，4，内环两个路口的数字分别为$-3$，2。要想进入迷宫中心需破解密码：内外环两个路口的数相乘，若乘积最大，沿这两个路口就可到达迷宫中心，则乘积最大的值是15。

答案： 14.15

15. 已知$|x| = 3$，$|y| = 7$。
(1)若$xy ＜ 0$，求$x - y$的值；
(2)若$x - y ＜ 0$，求$xy$的值。

答案： 15.解:
(1)
∵|x|=3,
∴x=±3.
∵|y|=7,
∴y=±7.
∵xy＜0,
∴x,y异号.
∴x=3,y=-7或x=-3,y=7.当x=3,y=-7时,x-y=3-(-7)=10;当x=-3,y=7时,x-y=-3-7=-10.
∴x-y的值是±10.
(2)
∵x=±3,y=±7,且x-y＜0,
∴x=3,y=7或x=-3,y=7.
∴xy的值是±21.