《2025年名校课堂七年级数学3上册人教版广东专版》

1. 角的概念：
有公共端点的两条射线组成的图形叫作角.

答案： 角

2. 角的换算：
1 周角$=$360$^{\circ}$，1 平角$=$180$^{\circ}$，$1^{\circ}=$60$'$，$1'=$60$''$.

答案： 2. 360　180　60　60

问题 1：类比线段长短的比较，除了用量角器量出角的度数，还可以将两个角的一边叠合在一起，两个角的另一边在重合边的同一侧，观察这两边的位置，比较这两个角的大小：

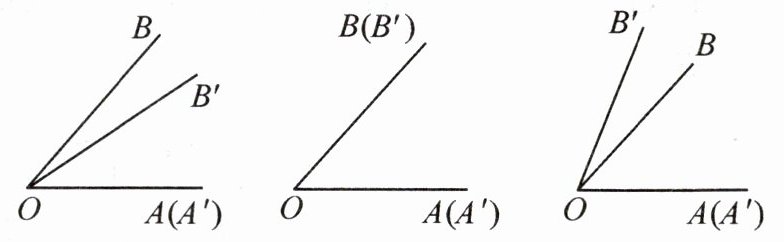
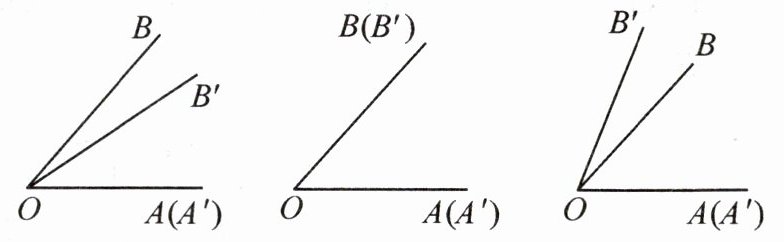
$\angle A'O'B'$＜$\angle AOB$ $\angle A'O'B'$=$\angle AOB$ $\angle A'O'B'$＞$\angle AOB$

答案： 问题1: ＜ = ＞

1. 如图，用“$＜$”或“$＞$”填空：

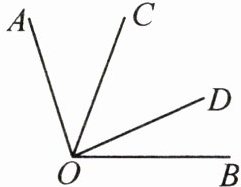
(1)$\angle AOD$＞$\angle AOC$；
(2)$\angle AOB$＞$\angle BOC$；
(3)$\angle COD$＜$\angle BOC$.

答案： 1.
(1)＞　
(2)＞　
(3)＜

问题 2：(1)如图，$\angle AOC$是$\angle AOB$与$\angle BOC$的和，记作：$\angle AOC=\angle AOB+\angle BOC$；
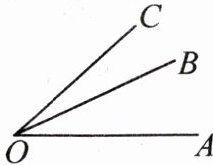
(2)$\angle AOB$是$\angle AOC$与$\angle BOC$的差，记作：∠AOB=∠AOC−∠BOC；
(3)类似地，$\angle AOC-\angle AOB=$∠BOC.

答案： 问题2:
(2)∠AOB=∠AOC−∠BOC　
(3)∠BOC

2. 如图，请填出符合下列等式的角：

(1)$\angle AOB+\angle BOC=$∠AOC；
(2)$\angle BOC=\angle BOD-$∠COD；
(3)$\angle AOD=\angle AOB+\angle COD+$∠BOC；
(4)$\angle DOB=\angle DOA-\angle COA+$∠BOC.

答案： 2.
(1)∠AOC　
(2)∠COD　
(3)∠BOC　
(4)∠BOC

3. 【例 1】(1)如图 1，若$\angle AOC=35^{\circ}$，$\angle BOC=40^{\circ}$，则$\angle AOB=\angle AOC+\angle$$=$；


(2)如图 2，若$\angle AOB=60^{\circ}$，$\angle BOC=40^{\circ}$，则$\angle AOC=$.

答案： 3.
(1)BOC　75°

4. 如图，填空：

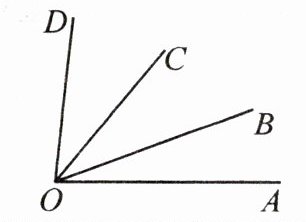
(1)若$\angle AOB=20^{\circ}$，$\angle BOC=30^{\circ}$，则$\angle AOC=$50°；
(2)若$\angle DOB=66^{\circ}55'$，$\angle BOC=28^{\circ}36'$，则$\angle COD=\angle DOB-\angle$BOC$=$38°19'.

答案： 4.
(1)50°　
(2)BOC　38°19'