《2025年新坐标同步练习七年级数学上册人教版青海专用》

13. 某市为倡导节约用水,制定了居民用水收费标准：如果每户每月用水量不超过 10 立方米,按每立方米 2 元收费；如果每户每月用水量超过 10 立方米,超出部分按每立方米 3.5 元收费. 另外每立方米水都要加收 1 元污水处理费. 小王家 6 月份付了 75 元水费,小王家这个月用了多少立方米水？

答案： 解:设小王家这个月用了x立方米水.因为10×(2+1)=30＜75,所以x＞10.由题意,得10×2+3.5(x-10)+x=75,解得x=20.答:小王家这个月用了20立方米水.

14. 某条城际铁路线共有 A,B,C 三个车站,每日上午均有两班次列车从 A 站驶往 C 站,其中 D1001 次列车从 A 站始发,经停 B 站后到达 C 站,G1002 次列车从 A 站始发,直达 C 站,两个车次的列车在行驶过程中保持各自的行驶速度不变. 某校数学学习小组对列车运行情况进行研究,收集到列车运行信息如表所示.


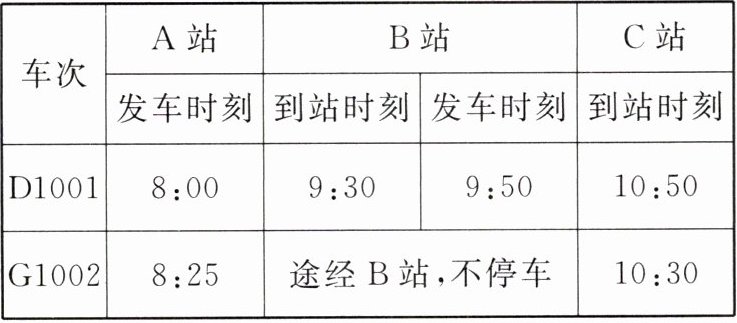
请根据表格中的信息,解答下列问题：
(1)D1001 次列车从 A 站到 B 站行驶了______分钟,从 B 站到 C 站行驶了______分钟.
(2)记 D1001 次列车的行驶速度为 $ v_1 $,离 A 站的路程为 $ d_1 $；G1002 次列车的行驶速度为 $ v_2 $,离 A 站的路程为 $ d_2 $.
① $ \frac{v_1}{v_2}= $______；
②从上午 8:00 开始计时,时长记为 $ t $ 分钟(如：上午 9:15,则 $ t = 75 $). 已知 $ v_1 = 240 $ 千米/小时(可换算为 4 千米/分钟),在 G1002 次列车的行驶过程中($ 25 \leq t \leq 150 $),若 $ |d_1 - d_2| = 60 $,求 $ t $ 的值.
(1)9060
(2)①$\frac{5}{6}$②因为v₁=4千米/分钟,又由①,知$\frac{v_{1}}{v_{2}}=\frac{5}{6}$,所以v₂=4.8千米/分钟.因为4×90=360(千米),所以A站与B站之间的路程为360千米.因为360÷4.8=75(分钟),所以当t=100时,G1002次列车经过B站.由题意可知,当90≤t≤110时,D1001次列车在B站停车,所以G1002次列车经过B站时,D1001次列车正在B站停车.(ⅰ)当25≤t＜90时,d₁＞d₂,所以|d₁-d₂|=d₁-d₂,所以4t-4.8(t-25)=60,解得t=75;(ⅱ)当90≤t≤100时,d₁≥d₂,所以|d₁-d₂|=d₁-d₂,所以360-4.8(t-25)=60,解得t=87.5,不合题意,舍去;(ⅲ)当100＜t≤110时,d₁＜d₂,所以|d₁-d₂|=d₂-d₁,所以4.8(t-25)-360=60,解得t=112.5,不合题意,舍去;(ⅳ)当110＜t≤150时,d₁＜d₂,所以|d₁-d₂|=d₂-d₁,所以4.8(t-25)-[360+4(t-110)]=60,解得t=125.综上所述,当t=75或125时,|d₁-d₂|=60.

答案： 解:
(1)90 60
(2)①$\frac{5}{6}$②因为v₁=4千米/分钟,又由①,知$\frac{v_{1}}{v_{2}}=\frac{5}{6}$,所以v₂=4.8千米/分钟.因为4×90=360(千米),所以A站与B站之间的路程为360千米.因为360÷4.8=75(分钟),所以当t=100时,G1002次列车经过B站.由题意可知,当90≤t≤110时,D1001次列车在B站停车,所以G1002次列车经过B站时,D1001次列车正在B站停车.(ⅰ)当25≤t＜90时,d₁＞d₂,所以|d₁-d₂|=d₁-d₂,所以4t-4.8(t-25)=60,解得t=75;(ⅱ)当90≤t≤100时,d₁≥d₂,所以|d₁-d₂|=d₁-d₂,所以360-4.8(t-25)=60,解得t=87.5,不合题意,舍去;(ⅲ)当100＜t≤110时,d₁＜d₂,所以|d₁-d₂|=d₂-d₁,所以4.8(t-25)-360=60,解得t=112.5,不合题意,舍去;(ⅳ)当110＜t≤150时,d₁＜d₂,所以|d₁-d₂|=d₂-d₁,所以4.8(t-25)-[360+4(t-110)]=60,解得t=125.综上所述,当t=75或125时,|d₁-d₂|=60.