2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
12. (浙江中考)不等式组 的解集为
的解集为
 的解集为
的解集为−2≤x<3
.
答案:
−2≤x<3
13. (湖南中考)已知直线$a // b$,将一块含$30^{\circ}角的直角三角板ABC$按如图所示方式放置($\angle BAC = 30^{\circ}$),并且顶点$A$,$C分别落在直线a$,$b$上,若$\angle 1 = 18^{\circ}$,则$\angle 2$的度数是__
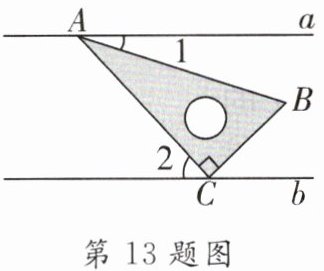
48°
__.
答案:
48°
14. 如图所示,$AB \perp CD$,且$AB = CD$.$E$,$F是AD$上两点,$CE \perp AD$,$BF \perp AD$.若$CE = a$,$BF = b$,$EF = c$,则$AD$的长为______.
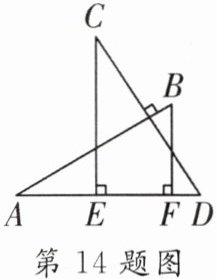
14. 如图所示,$AB \perp CD$,且$AB = CD$.$E$,$F是AD$上两点,$CE \perp AD$,$BF \perp AD$.若$CE = a$,$BF = b$,$EF = c$,则$AD$的长为

14. 如图所示,$AB \perp CD$,且$AB = CD$.$E$,$F是AD$上两点,$CE \perp AD$,$BF \perp AD$.若$CE = a$,$BF = b$,$EF = c$,则$AD$的长为
a+b−c
.
答案:
a+b−c
15. (2022·盘锦)从不等式组$\begin{cases}2x + 3 \leq x + 9,\frac{2x + 4}{3} - 1 > 2 - x\end{cases} $所有整数解中任取一个数,它是偶数的概率是______
$\frac{3}{5}$
.
答案:
$\frac{3}{5}$
16. (8分)(2024·四川模拟)解不等式,并把它的解集在数轴上表示出来.
$\frac{x - 2}{5} - \frac{x + 4}{2} > - 3$

$\frac{x - 2}{5} - \frac{x + 4}{2} > - 3$

答案:
解:去分母,得2(x−2)−5(x+4)>−30.
去括号,得2x−4−5x−20>−30.
移项,得2x−5x>−30+4+20.
合并同类项,得−3x>−6.
系数化为1,得x<2.
将不等式解集表示在数轴上如下:

解:去分母,得2(x−2)−5(x+4)>−30.
去括号,得2x−4−5x−20>−30.
移项,得2x−5x>−30+4+20.
合并同类项,得−3x>−6.
系数化为1,得x<2.
将不等式解集表示在数轴上如下:

17. (8分)解不等式组:
解:解不等式$\frac{x}{2}$−$\frac{x−1}{3}$≥1,得
解不等式$\frac{x−3}{2}$<x+2,得
则不等式组的解集为
解:解不等式$\frac{x}{2}$−$\frac{x−1}{3}$≥1,得
x≥4
.解不等式$\frac{x−3}{2}$<x+2,得
x>−7
.则不等式组的解集为
x≥4
.
答案:
解:解不等式$\frac{x}{2}$−$\frac{x−1}{3}$≥1,得x≥4.
解不等式$\frac{x−3}{2}$<x+2,得x>−7.
则不等式组的解集为x≥4.
解不等式$\frac{x−3}{2}$<x+2,得x>−7.
则不等式组的解集为x≥4.
18. (8分)如图所示,$\triangle ABC$中,$AD平分\angle BAC$,$DG \perp BC且平分BC$,$DE \perp AB于E$,$DF \perp AC于F$.
(1)说明$BE = CF$的理由;
(2)如果$AB = 5$,$AC = 3$,求$AE$,$BE$的长.
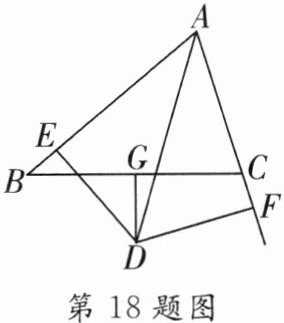
(1)说明$BE = CF$的理由;
(2)如果$AB = 5$,$AC = 3$,求$AE$,$BE$的长.

答案:
解:
(1)证明:如图所示,连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°.
∵DG⊥BC且平分BC,
∴BD=CD.
在Rt△BED与Rt△CFD中,
$\begin{cases} DB = CD, \\ DE = DF, \end{cases}$

∴Rt△BED≌Rt△CFD (HL).
∴BE=CF.
(2)解:在△AED和△AFD中,
$\begin{cases} \angle AED = \angle AFD = 90^{\circ}, \\ \angle EAD = \angle FAD, \\ AD = AD, \end{cases}$
∴△AED≌△AFD(AAS).
∴AE=AF.
设BE=x,则CF=x.
∵AB=5,AC=3,AE=AB−BE,AF=AC+CF,
∴5−x=3+x.
解得x=1.
∴BE=1,AE=AB−BE=5−1=4.
解:
(1)证明:如图所示,连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°.
∵DG⊥BC且平分BC,
∴BD=CD.
在Rt△BED与Rt△CFD中,
$\begin{cases} DB = CD, \\ DE = DF, \end{cases}$

∴Rt△BED≌Rt△CFD (HL).
∴BE=CF.
(2)解:在△AED和△AFD中,
$\begin{cases} \angle AED = \angle AFD = 90^{\circ}, \\ \angle EAD = \angle FAD, \\ AD = AD, \end{cases}$
∴△AED≌△AFD(AAS).
∴AE=AF.
设BE=x,则CF=x.
∵AB=5,AC=3,AE=AB−BE,AF=AC+CF,
∴5−x=3+x.
解得x=1.
∴BE=1,AE=AB−BE=5−1=4.
19. (9分)如图所示,在$\triangle ABC$中,$AB = AC$,$AD是BC$边上的中线,$BE \perp AC于点E$.
求证:$\angle CBE = \angle BAD$.
证明:∵AB=AC,
∴∠ABC=∠C.
又∵AD是BC边上的中线,
∴AD⊥BC.
∴∠BAD+∠ABC=90°.
∵BE⊥AC,
∴∠CBE+∠C=90°.
∴

求证:$\angle CBE = \angle BAD$.
证明:∵AB=AC,
∴∠ABC=∠C.
又∵AD是BC边上的中线,
∴AD⊥BC.
∴∠BAD+∠ABC=90°.
∵BE⊥AC,
∴∠CBE+∠C=90°.
∴
∠CBE=∠BAD
.
答案:
证明:
∵AB=AC,
∴∠ABC=∠C.
又
∵AD是BC边上的中线,
∴AD⊥BC.
∴∠BAD+∠ABC=90°.
∵BE⊥AC,
∴∠CBE+∠C=90°.
∴∠CBE=∠BAD.
∵AB=AC,
∴∠ABC=∠C.
又
∵AD是BC边上的中线,
∴AD⊥BC.
∴∠BAD+∠ABC=90°.
∵BE⊥AC,
∴∠CBE+∠C=90°.
∴∠CBE=∠BAD.
20. (12分)(山东中考)有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
答案:
解:
(1)设1辆甲种客车与1辆乙种客车的载客量分别为x人,y人.
$\begin{cases} 2x + 3y = 180, \\ x + 2y = 105. \end{cases}$
解得$\begin{cases} x = 45, \\ y = 30. \end{cases}$
答:1辆甲种客车与1辆乙种客车的载客量分别为45人和30人.
(2)设租用甲种客车a辆.
依题意得$\begin{cases} 45a + 30(6 - a) \geqslant 240, \\ a < 6, \end{cases}$ 解得6>a≥4.
因为a取整数,
所以a=4或5.
∵5×400+1×280>4×400+2×280,
∴a=4时,租车费用最低,为4×400+2×280=2160元
(1)设1辆甲种客车与1辆乙种客车的载客量分别为x人,y人.
$\begin{cases} 2x + 3y = 180, \\ x + 2y = 105. \end{cases}$
解得$\begin{cases} x = 45, \\ y = 30. \end{cases}$
答:1辆甲种客车与1辆乙种客车的载客量分别为45人和30人.
(2)设租用甲种客车a辆.
依题意得$\begin{cases} 45a + 30(6 - a) \geqslant 240, \\ a < 6, \end{cases}$ 解得6>a≥4.
因为a取整数,
所以a=4或5.
∵5×400+1×280>4×400+2×280,
∴a=4时,租车费用最低,为4×400+2×280=2160元
查看更多完整答案,请扫码查看


