《2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制》

14.如果不等式组$\begin{cases}x ＜ 5,\\x ＞ m\end{cases} $有解,那么$m$的取值范围是____$ m ＜ 5 $。

答案： $ m ＜ 5 $

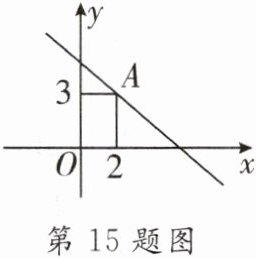
15.如图所示,一次函数$y = kx + b(k ＜ 0)$的图象经过点$A$,当$y ＜ 3$时,$x$的取值范围是____$ x ＞ 2 $。

答案： $ x ＞ 2 $

16.(2023·广东)某商品进价4元,标价5元出售,商家准备打折销售,但其利润率不能少于$10\%$,则最多可打8.8折。

答案： 8.8

17.(6分)(2022·扬州)解不等式组$\begin{cases}x - 2 \leq 2x,\\x - 1 ＜ \frac{1 + 2x}{3},\end{cases} $并求出它的所有整数解的和。

答案： 解：$\begin{cases}x - 2 \leq 2x, ① \\ x - 1 ＜ \frac{1 + 2x}{3}, ②\end{cases}$
解不等式①，得 $ x \geq -2 $。
解不等式②，得 $ x ＜ 4 $。
∴原不等式组的解集是 $ -2 \leq x ＜ 4 $。
∴该不等式组的整数解是 $ -2, -1, 0, 1, 2, 3 $，
∵ $ -2 + (-1) + 0 + 1 + 2 + 3 = 3 $，
∴该不等式组所有整数解的和是 3。

18.(6分)(2024·湖北模拟)若点$P的坐标为(\frac{x - 1}{3},2x - 9)$,其中$x满足不等式组\begin{cases}5x - 10 \geq 2(x + 1),\frac{1}{2}x - 1 \leq 7 - \frac{3}{2}x,\end{cases} 求点P$所在的象限。

答案： 解：$\begin{cases}5x - 10 \geq 2(x + 1), ① \\ \frac{1}{2}x - 1 \leq 7 - \frac{3}{2}x, ②\end{cases}$
解①得：$ x \geq 4 $，
解②得：$ x \leq 4 $，
则不等式组的解是：$ x = 4 $，
∵ $ \frac{x - 1}{3} = 1, 2x - 9 = -1 $，
∴点 $ P $ 的坐标为 $ (1, -1) $，
∴点 $ P $ 在的第四象限。

19.(8分)(辽宁中考)某市政部门为了保护生态环境,计划购买$A$,$B$两种型号的环保设备。已知购买一套$A型设备和三套B$型设备共需230万元,购买三套$A型设备和两套B$型设备共需340万元。
(1)求$A型设备和B$型设备的单价各是多少万元；
(2)根据需要市政部门采购$A型和B$型设备共50套,预算资金不超过3000万元,问最多可购买$A$型设备多少套？

答案： 解：
(1)设 $ A $ 型设备的单价是 $ x $ 万元，$ B $ 型设备的单价是 $ y $ 万元。
依题意，得 $\begin{cases}x + 3y = 230, \\ 3x + 2y = 340.\end{cases}$
解得 $\begin{cases}x = 80, \\ y = 50.\end{cases}$
答：$ A $ 型设备的单价是 80 万元，$ B $ 型设备的单价是 50 万元。
(2)设购进 $ A $ 型设备 $ m $ 套，则购进 $ B $ 型设备 $ (50 - m) $ 套。
依题意，得 $ 80m + 50(50 - m) \leq 3000 $，
解得 $ m \leq \frac{50}{3} $。
∵ $ m $ 为整数，
∴ $ m $ 的最大值为 16。
答：最多可购买 $ A $ 型设备 16 套。

20.(8分)(2022·宿迁)某单位准备购买文化用品,现有甲、乙两家超市进行促销活动,该文化用品两家超市的标价均为10元/件,甲超市一次性购买金额不超过400元的不优惠,超过400元的部分按标价的6折售卖；乙超市全部按标价的8折售卖。
(1)若该单位需要购买30件这种文化用品,则在甲超市的购物金额为____300元；乙超市的购物金额为____240元；
(2)假如你是该单位的采购员,你认为选择哪家超市支付的费用较少？
解：设单位购买 $ x $ 件这种文化用品，所花费用为 $ y $ 元。又当 $ 10x = 400 $ 时，可得 $ x = 40 $，
①当 $ 0 ＜ x \leq 40 $ 时，$ y_{甲} = 10x $，$ y_{乙} = 0.8 × 10x = 8x $，显然此时选择乙超市更优惠。
②当 $ x ＞ 40 $ 时，$ y_{甲} = 400 + 0.6 × 10(x - 40) = 6x + 160 $，$ y_{乙} = 0.8 × 10x = 8x $。
i 当 $ y_{甲} = y_{乙} $ 时，则 $ 8x = 6x + 160 $，解得 $ x = 80 $，
∴当 $ x = 80 $ 时，两家超市的优惠一样。
ii 当 $ y_{甲} ＞ y_{乙} $ 时，则 $ 6x + 160 ＞ 8x $，解得 $ x ＜ 80 $，
∴当 $ 40 ＜ x ＜ 80 $ 时，选择乙超市更优惠。
iii 当 $ y_{甲} ＜ y_{乙} $ 时，则 $ 6x + 160 ＜ 8x $，解得 $ x ＞ 80 $，
∴当 $ x ＞ 80 $ 时，选择甲超市更优惠。
综上所述，当 $ 0 ＜ x ＜ 80 $ 时，选择乙超市更优惠；当 $ x = 80 $ 时，选择甲，乙超市一样优惠；当 $ x ＞ 80 $ 时，选择甲超市更优惠。

答案： 解：
(1)
∵甲超市一次性购买金额不超过 400 元的不优惠，超过 400 元的部分按标价的 6 折售卖；
∴该单位需要购买 30 件这种文化用品，则在甲超市的购物金额为 $ 30 × 10 = 300 $（元）。
∵乙超市全部按标价的 8 折售卖，
∴该单位需要购买 30 件这种文化用品，则在乙超市的购物金额为 $ 30 × 10 × 0.8 = 240 $（元）。
故答案为：300，240。
(2)设单位购买 $ x $ 件这种文化用品，所花费用为 $ y $ 元。又当 $ 10x = 400 $ 时，可得 $ x = 40 $，
①当 $ 0 ＜ x \leq 40 $ 时，$ y_{甲} = 10x $，$ y_{乙} = 0.8 × 10x = 8x $，显然此时选择乙超市更优惠。
②当 $ x ＞ 40 $ 时，$ y_{甲} = 400 + 0.6 × 10(x - 40) = 6x + 160 $，$ y_{乙} = 0.8 × 10x = 8x $。
i 当 $ y_{甲} = y_{乙} $ 时，则 $ 8x = 6x + 160 $，解得 $ x = 80 $，
∴当 $ x = 80 $ 时，两家超市的优惠一样。
ii 当 $ y_{甲} ＞ y_{乙} $ 时，则 $ 6x + 160 ＞ 8x $，解得 $ x ＜ 80 $，
∴当 $ 40 ＜ x ＜ 80 $ 时，选择乙超市更优惠。
iii 当 $ y_{甲} ＜ y_{乙} $ 时，则 $ 6x + 160 ＜ 8x $，解得 $ x ＞ 80 $，
∴当 $ x ＞ 80 $ 时，选择甲超市更优惠。
综上所述，当 $ 0 ＜ x ＜ 80 $ 时，选择乙超市更优惠；当 $ x = 80 $ 时，选择甲，乙超市一样优惠；当 $ x ＞ 80 $ 时，选择甲超市更优惠。