2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页

答案:
①垂直且平分一条线段;②垂直平分线;③这条线段两个端点的距离相等;④$PA = PB$;⑤与一条线段两个端点距离相等的点;⑥三个顶点的距离相等。
1.(2023·凉山州)如图,在等腰△ABC中,∠A= 40°,分别以点A、点B为圆心,大于$\frac{1}{2}AB$的长为半径画弧,两弧分别交于点M和点N,连接MN,直线MN与AC交于点D,连接BD,则∠DBC的度数是(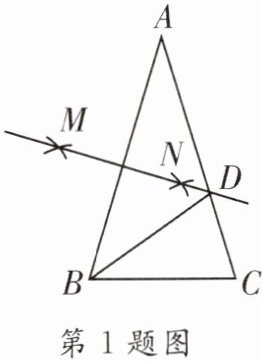
A.20°
B.30°
C.40°
D.50°
B
)
A.20°
B.30°
C.40°
D.50°
答案:
B
2.(湖北中考)如图所示,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B= 60°,∠C= 25°,则∠BAD为(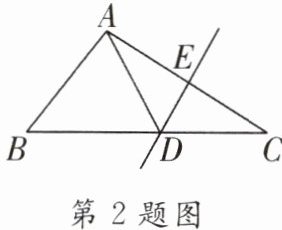
A.50°
B.70°
C.75°
D.80°
B
)
A.50°
B.70°
C.75°
D.80°
答案:
B
有5只猴子在山上发现了一处野生桃林.它们摘下一些桃子堆在一起,并且决定第二天来平分这些桃子.第二天清晨﹐有一只猴子来得最早,它左分右分分不开,就吃了一个,这时剩下的桃子刚好可以分成5份,于是这只猴子带上自己的一份走了.接下来的每一只猴子都遇到了相同的问题,并采取了同样的方法。也就是说,每只猴子都吃掉了一个桃子后·剩下的挑子刚好可以分成5份.请问;这堆桃子最初至少有
3121
个?
答案:
1. 设最初有$x$个桃子:
第一只猴子吃了$1$个后,剩下$(x - 1)$个,它拿走一份后剩下$\frac{4}{5}(x - 1)$个;
第二只猴子吃了$1$个后,剩下$\frac{4}{5}(x - 1)-1=\frac{4x-4 - 5}{5}=\frac{4x - 9}{5}$个,它拿走一份后剩下$\frac{4}{5}×(\frac{4x - 9}{5})=\frac{16x-36 - 25}{25}=\frac{16x - 61}{25}$个;
第三只猴子吃了$1$个后,剩下$\frac{16x - 61}{25}-1=\frac{16x-61 - 25}{25}=\frac{16x - 86}{25}$个,它拿走一份后剩下$\frac{4}{5}×(\frac{16x - 86}{25})=\frac{64x-344 - 125}{125}=\frac{64x - 469}{125}$个;
第四只猴子吃了$1$个后,剩下$\frac{64x - 469}{125}-1=\frac{64x-469 - 125}{125}=\frac{64x - 594}{125}$个,它拿走一份后剩下$\frac{4}{5}×(\frac{64x - 594}{125})=\frac{256x-2376 - 625}{625}=\frac{256x - 3001}{625}$个;
第五只猴子吃了$1$个后,剩下$\frac{256x - 3001}{625}-1=\frac{256x-3001 - 625}{625}=\frac{256x - 3626}{625}$个,它拿走一份后剩下$\frac{4}{5}×(\frac{256x - 3626}{625})=\frac{1024x-14504 - 1875}{3125}=\frac{1024x - 16379}{3125}$个。
2. 令$y=\frac{1024x - 16379}{3125}$($y$为整数):
则$1024x-16379 = 3125y$,$x=\frac{3125y + 16379}{1024}=\frac{3125y+3125×5 + 724}{1024}=\frac{3125(y + 5)+724}{1024}$。
因为$3125\equiv1\pmod{1024}$($3125÷1024 = 3\cdots\cdots53$,$1024×3+53 = 3125$,$3125-1024×3=53$,$53×19 = 1007$,$1024 - 1007 = 17$,$53×20=1060$,$1060-1024 = 36$,通过计算$3125÷1024$的余数,$3125 = 1024×3+53$,$53×19 = 1007$,$1024×19+53×19=1024×19 + 1007=1024×20 - 17$,$53×20=1060$,$1060 - 1024 = 36$,$3125\equiv1\pmod{1024}$),所以$x=\frac{3125(y + 5)+724}{1024}$,要使$x$为整数,当$y + 5$能被$1024$整除时,$x$最小。
令$y+5 = 1024$,$y = 1019$。
则$x=\frac{3125×1024+16379}{1024}=3125+\frac{16379}{1024}$。
另一种方法:
我们可以从后往前推,设最后一只猴子分桃前有$x_5$个桃子,因为它吃$1$个后能分成$5$份,设每份为$a_5$个,则$x_5=5a_5 + 1$。
第四只猴子分桃前有$x_4$个桃子,$x_4=\frac{5}{4}(x_5)+1=\frac{5}{4}(5a_5 + 1)+1=\frac{25a_5+5 + 4}{4}=\frac{25a_5+9}{4}$。
第三只猴子分桃前有$x_3$个桃子,$x_3=\frac{5}{4}(x_4)+1=\frac{5}{4}(\frac{25a_5+9}{4})+1=\frac{125a_5+45 + 16}{16}=\frac{125a_5+61}{16}$。
第二只猴子分桃前有$x_2$个桃子,$x_2=\frac{5}{4}(x_3)+1=\frac{5}{4}(\frac{125a_5+61}{16})+1=\frac{625a_5+305 + 64}{64}=\frac{625a_5+369}{64}$。
第一只猴子分桃前有$x_1$个桃子,$x_1=\frac{5}{4}(x_2)+1=\frac{5}{4}(\frac{625a_5+369}{64})+1=\frac{3125a_5+1845 + 256}{256}=\frac{3125a_5+2101}{256}$。
我们要找到最小的正整数$a_5$使得$x_1$为整数。
我们可以利用同余的性质,设$x$满足$x\equiv1\pmod{5}$,$\frac{4}{5}(x - 1)\equiv1\pmod{5}$,$\frac{4}{5}(\frac{4}{5}(x - 1)-1)\equiv1\pmod{5}$,$\cdots$。
设$x + 4$是$5^5$的倍数(通过找规律,假设$x = 5^5-4$)。
因为$5^5=3125$。
解:
设最初桃子数为$x$,根据题意,我们可以通过递推关系或者利用同余的性质来求解。
假设$x+4$是$5^5$的倍数(从每只猴子分桃的规律来看,$x + 4$能被$5$,$5^2$,$5^3$,$5^4$,$5^5$整除)。
因为$5^5=3125$,所以$x=5^5-4$。
计算$x = 3125-4=3121$。
所以这堆桃子最初至少有$3121$个。
第一只猴子吃了$1$个后,剩下$(x - 1)$个,它拿走一份后剩下$\frac{4}{5}(x - 1)$个;
第二只猴子吃了$1$个后,剩下$\frac{4}{5}(x - 1)-1=\frac{4x-4 - 5}{5}=\frac{4x - 9}{5}$个,它拿走一份后剩下$\frac{4}{5}×(\frac{4x - 9}{5})=\frac{16x-36 - 25}{25}=\frac{16x - 61}{25}$个;
第三只猴子吃了$1$个后,剩下$\frac{16x - 61}{25}-1=\frac{16x-61 - 25}{25}=\frac{16x - 86}{25}$个,它拿走一份后剩下$\frac{4}{5}×(\frac{16x - 86}{25})=\frac{64x-344 - 125}{125}=\frac{64x - 469}{125}$个;
第四只猴子吃了$1$个后,剩下$\frac{64x - 469}{125}-1=\frac{64x-469 - 125}{125}=\frac{64x - 594}{125}$个,它拿走一份后剩下$\frac{4}{5}×(\frac{64x - 594}{125})=\frac{256x-2376 - 625}{625}=\frac{256x - 3001}{625}$个;
第五只猴子吃了$1$个后,剩下$\frac{256x - 3001}{625}-1=\frac{256x-3001 - 625}{625}=\frac{256x - 3626}{625}$个,它拿走一份后剩下$\frac{4}{5}×(\frac{256x - 3626}{625})=\frac{1024x-14504 - 1875}{3125}=\frac{1024x - 16379}{3125}$个。
2. 令$y=\frac{1024x - 16379}{3125}$($y$为整数):
则$1024x-16379 = 3125y$,$x=\frac{3125y + 16379}{1024}=\frac{3125y+3125×5 + 724}{1024}=\frac{3125(y + 5)+724}{1024}$。
因为$3125\equiv1\pmod{1024}$($3125÷1024 = 3\cdots\cdots53$,$1024×3+53 = 3125$,$3125-1024×3=53$,$53×19 = 1007$,$1024 - 1007 = 17$,$53×20=1060$,$1060-1024 = 36$,通过计算$3125÷1024$的余数,$3125 = 1024×3+53$,$53×19 = 1007$,$1024×19+53×19=1024×19 + 1007=1024×20 - 17$,$53×20=1060$,$1060 - 1024 = 36$,$3125\equiv1\pmod{1024}$),所以$x=\frac{3125(y + 5)+724}{1024}$,要使$x$为整数,当$y + 5$能被$1024$整除时,$x$最小。
令$y+5 = 1024$,$y = 1019$。
则$x=\frac{3125×1024+16379}{1024}=3125+\frac{16379}{1024}$。
另一种方法:
我们可以从后往前推,设最后一只猴子分桃前有$x_5$个桃子,因为它吃$1$个后能分成$5$份,设每份为$a_5$个,则$x_5=5a_5 + 1$。
第四只猴子分桃前有$x_4$个桃子,$x_4=\frac{5}{4}(x_5)+1=\frac{5}{4}(5a_5 + 1)+1=\frac{25a_5+5 + 4}{4}=\frac{25a_5+9}{4}$。
第三只猴子分桃前有$x_3$个桃子,$x_3=\frac{5}{4}(x_4)+1=\frac{5}{4}(\frac{25a_5+9}{4})+1=\frac{125a_5+45 + 16}{16}=\frac{125a_5+61}{16}$。
第二只猴子分桃前有$x_2$个桃子,$x_2=\frac{5}{4}(x_3)+1=\frac{5}{4}(\frac{125a_5+61}{16})+1=\frac{625a_5+305 + 64}{64}=\frac{625a_5+369}{64}$。
第一只猴子分桃前有$x_1$个桃子,$x_1=\frac{5}{4}(x_2)+1=\frac{5}{4}(\frac{625a_5+369}{64})+1=\frac{3125a_5+1845 + 256}{256}=\frac{3125a_5+2101}{256}$。
我们要找到最小的正整数$a_5$使得$x_1$为整数。
我们可以利用同余的性质,设$x$满足$x\equiv1\pmod{5}$,$\frac{4}{5}(x - 1)\equiv1\pmod{5}$,$\frac{4}{5}(\frac{4}{5}(x - 1)-1)\equiv1\pmod{5}$,$\cdots$。
设$x + 4$是$5^5$的倍数(通过找规律,假设$x = 5^5-4$)。
因为$5^5=3125$。
解:
设最初桃子数为$x$,根据题意,我们可以通过递推关系或者利用同余的性质来求解。
假设$x+4$是$5^5$的倍数(从每只猴子分桃的规律来看,$x + 4$能被$5$,$5^2$,$5^3$,$5^4$,$5^5$整除)。
因为$5^5=3125$,所以$x=5^5-4$。
计算$x = 3125-4=3121$。
所以这堆桃子最初至少有$3121$个。
查看更多完整答案,请扫码查看


