2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
高明的蜂王
有一群蜜蜂·每天辛勤地采蜜.如果它们归巢时蜂拥而入,就会拥挤碰伤.聪明的蜂王想了一个办法:把蜜蜂分成三群﹐第一群50分钟归巢一次﹔第二群60分钟归巢一次。这样就避免了全体同时归巢的情况发生.你能说明这是为什么吗?
有一群蜜蜂·每天辛勤地采蜜.如果它们归巢时蜂拥而入,就会拥挤碰伤.聪明的蜂王想了一个办法:把蜜蜂分成三群﹐第一群50分钟归巢一次﹔第二群60分钟归巢一次。这样就避免了全体同时归巢的情况发生.你能说明这是为什么吗?
如果早上9时﹐蜜蜂倾巢而出﹐要到35小时以后﹐即第二天晚上8时才会出现全体同时归巢的情况﹐而蜜蜂晚上不工作﹐因此不必担心拥挤了。
答案:
答案:如果早上9时﹐蜜蜂倾巢而出﹐要到35小时以后﹐即第二天晚上8时才会出现全体同时归巢的情况﹐而蜜蜂晚上不工作﹐因此不必担心拥挤了.
3. 如图所示,在△ABC中,AB的垂直平分线交BC于D,AC的中垂线交BC于E,∠DAE= 20°,则∠BAC的度数为(

A.70°
B.80°
C.90°
D.100°
D
)
A.70°
B.80°
C.90°
D.100°
答案:
D
4. 如图,D是线段AC,AB的垂直平分线的交点,若∠ACD= 30°,∠BAD= 50°,则∠BCD的大小是(

A.10°
B.20°
C.30°
D.40°
A
)
A.10°
B.20°
C.30°
D.40°
答案:
A
5.(2022·丹东)如图,在Rt△ABC中,∠B= 90°,AB= 4,BC= 8,分别以A,C为圆心,以大于$\frac{1}{2}AC$的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为______.

5.(2022·丹东)如图,在Rt△ABC中,∠B= 90°,AB= 4,BC= 8,分别以A,C为圆心,以大于$\frac{1}{2}AC$的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为______.

5.(2022·丹东)如图,在Rt△ABC中,∠B= 90°,AB= 4,BC= 8,分别以A,C为圆心,以大于$\frac{1}{2}AC$的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为______.

5.(2022·丹东)如图,在Rt△ABC中,∠B= 90°,AB= 4,BC= 8,分别以A,C为圆心,以大于$\frac{1}{2}AC$的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为______.

5.(2022·丹东)如图,在Rt△ABC中,∠B= 90°,AB= 4,BC= 8,分别以A,C为圆心,以大于$\frac{1}{2}AC$的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为______.

5.(2022·丹东)如图,在Rt△ABC中,∠B= 90°,AB= 4,BC= 8,分别以A,C为圆心,以大于$\frac{1}{2}AC$的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为


5.(2022·丹东)如图,在Rt△ABC中,∠B= 90°,AB= 4,BC= 8,分别以A,C为圆心,以大于$\frac{1}{2}AC$的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为______.

5.(2022·丹东)如图,在Rt△ABC中,∠B= 90°,AB= 4,BC= 8,分别以A,C为圆心,以大于$\frac{1}{2}AC$的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为______.

5.(2022·丹东)如图,在Rt△ABC中,∠B= 90°,AB= 4,BC= 8,分别以A,C为圆心,以大于$\frac{1}{2}AC$的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为______.

5.(2022·丹东)如图,在Rt△ABC中,∠B= 90°,AB= 4,BC= 8,分别以A,C为圆心,以大于$\frac{1}{2}AC$的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为______.

5.(2022·丹东)如图,在Rt△ABC中,∠B= 90°,AB= 4,BC= 8,分别以A,C为圆心,以大于$\frac{1}{2}AC$的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为
$2\sqrt{5}$
.
答案:
$2\sqrt{5}$
6.(2021·广州)如图,在Rt△ABC中,∠C= 90°,∠A= 30°,线段AB的垂直平分线分别交AC,AB于点D,E,连接BD. 若CD= 1,则AD的长为______.

6.(2021·广州)如图,在Rt△ABC中,∠C= 90°,∠A= 30°,线段AB的垂直平分线分别交AC,AB于点D,E,连接BD. 若CD= 1,则AD的长为______.

6.(2021·广州)如图,在Rt△ABC中,∠C= 90°,∠A= 30°,线段AB的垂直平分线分别交AC,AB于点D,E,连接BD. 若CD= 1,则AD的长为

6.(2021·广州)如图,在Rt△ABC中,∠C= 90°,∠A= 30°,线段AB的垂直平分线分别交AC,AB于点D,E,连接BD. 若CD= 1,则AD的长为______.

6.(2021·广州)如图,在Rt△ABC中,∠C= 90°,∠A= 30°,线段AB的垂直平分线分别交AC,AB于点D,E,连接BD. 若CD= 1,则AD的长为
2
.
答案:
2
7.(2023·营口)如图,在△ABC中,以点A为圆心,AC长为半径作弧,交BC于C,D两点,分别以点C和点D为圆心,大于$\frac{1}{2}CD$长为半径作弧,两弧交于点P,作直线AP,交CD于点E,若AC= 5,CD= 6,则AE=
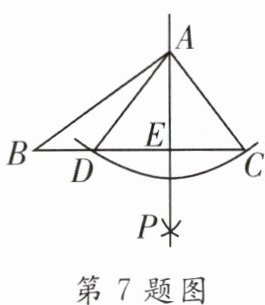
4
.
答案:
4
8. 如图所示,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC= 55°,则∠B的度数为______.

8. 如图所示,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC= 55°,则∠B的度数为

8. 如图所示,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC= 55°,则∠B的度数为
$55^{\circ}$
.
答案:
$55^{\circ}$
9. 如图所示,A,B,C三点表示三个村庄,为了解决村民子女就近入学的问题,有关部门计划建一所小学,要使学校到三个村庄的距离相等,学校的位置应设在何处?请说明理由.

答案:
解:如图所示,连接AC,AB,BC;作AC,AB的垂直平分线交于点P,所以学校的位置应设在P点。
理由:连接AP,BP,CP.
∵PE是AB的垂直平分线,
∴$PA=PB$.
∵PF是AC的垂直平分线,
∴$PA=PC$;
∴$PA=PB=PC$;

解:如图所示,连接AC,AB,BC;作AC,AB的垂直平分线交于点P,所以学校的位置应设在P点。
理由:连接AP,BP,CP.
∵PE是AB的垂直平分线,
∴$PA=PB$.
∵PF是AC的垂直平分线,
∴$PA=PC$;
∴$PA=PB=PC$;

10. 如图所示,在△ABC中,边AB,AC的垂直平分线分别交BC于D,E.
(1)若BC= 5,求△ADE的周长;
解:∵边AB,AC的垂直平分线分别交BC于D,E,
∴
∴$\triangle ADE$的周长$=AD+DE+AE=DB+DE+EC=BC=5$.
(2)若∠BAD+∠CAE= 60°,求∠BAC的度数.
解:∵
∴
∴
∴
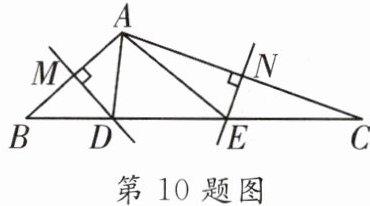
(1)若BC= 5,求△ADE的周长;
解:∵边AB,AC的垂直平分线分别交BC于D,E,
∴
$DA=DB$,$EA=EC$
.∴$\triangle ADE$的周长$=AD+DE+AE=DB+DE+EC=BC=5$.
(2)若∠BAD+∠CAE= 60°,求∠BAC的度数.
解:∵
$DA=DB$,$EA=EC$
,∴
$∠DAB=∠B$,$∠EAC=∠C$
;∴
$∠B+∠C=∠DAB+∠EAC=60^{\circ}$
.∴
$∠BAC=120^{\circ}$
.
答案:
解:
(1)
∵边AB,AC的垂直平分线分别交BC于D,E,
∴$DA=DB$,$EA=EC$.
∴$\triangle ADE$的周长$=AD+DE+AE=DB+DE+EC=BC=5$.
(2)
∵$DA=DB$,$EA=EC$,
∴$∠DAB=∠B$,$∠EAC=∠C$;
∴$∠B+∠C=∠DAB+∠EAC=60^{\circ}$.
∴$∠BAC=120^{\circ}$.
(1)
∵边AB,AC的垂直平分线分别交BC于D,E,
∴$DA=DB$,$EA=EC$.
∴$\triangle ADE$的周长$=AD+DE+AE=DB+DE+EC=BC=5$.
(2)
∵$DA=DB$,$EA=EC$,
∴$∠DAB=∠B$,$∠EAC=∠C$;
∴$∠B+∠C=∠DAB+∠EAC=60^{\circ}$.
∴$∠BAC=120^{\circ}$.
11. 如图所示,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB= CD,∠ABD= 120°,∠CDB= 38°,求∠OBD的度数.


答案:
解:如图所示,连接OA,OC.
∵OE,OF分别是AC,BD的垂直平分线,
∴$OA=OC$,$OB=OD$.
∵$AB=CD$,
∴$\triangle ABO≌\triangle CDO(SSS)$.
∴$∠ABO=∠CDO$.
设$∠OBD=∠ODB=α$,$∠ABO=∠CDO=β$.
∴$α+β=120^{\circ}$,$β - α=38^{\circ}$.
∴$α=41^{\circ}$.
∴$∠OBD=41^{\circ}$.

解:如图所示,连接OA,OC.
∵OE,OF分别是AC,BD的垂直平分线,
∴$OA=OC$,$OB=OD$.
∵$AB=CD$,
∴$\triangle ABO≌\triangle CDO(SSS)$.
∴$∠ABO=∠CDO$.
设$∠OBD=∠ODB=α$,$∠ABO=∠CDO=β$.
∴$α+β=120^{\circ}$,$β - α=38^{\circ}$.
∴$α=41^{\circ}$.
∴$∠OBD=41^{\circ}$.

查看更多完整答案,请扫码查看


