《2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制》

角平分线
趣味数学：
信装错的可能性有多少种
欧洲数学家雅各布·伯努利收到一位朋友的来信,打开一看信不是写给他的,但是信封上的地址、姓名又没有问题,觉得很奇怪.过了几天,他收到了这位朋友的道歉信.这位朋友在信中向他解释说：“写了5封信,又写好了5个信封,然后让仆人把信寄出.可是那位仆人在把信装到信封里时居然把它们全部都装错了！”看完信后他不禁哈哈大笑.不过他马上想到了一个问题：5封信装入写有不同地址和姓名的5个信封,全部装错的可能性有多少种？(全部装错的可能性有44种)

答案： 【解析】：本题可利用错位排列的递推公式来求解。错位排列是指把 $n$ 个元素的位置重新排列，使每个元素都不在原来位置上的排列问题。设 $n$ 封信全部装错的情况数记为 $D_n$，则有递推公式 $D_n=(n - 1)(D_{n - 1}+D_{n - 2})$ ，且 $D_1 = 0$，$D_2 = 1$。
当 $n = 3$ 时，$D_3=(3 - 1)×(D_{2}+D_{1})=2×(1 + 0)=2$；
当 $n = 4$ 时，$D_4=(4 - 1)×(D_{3}+D_{2})=3×(2 + 1)=9$；
当 $n = 5$ 时，$D_5=(5 - 1)×(D_{4}+D_{3})=4×(9 + 2)=44$。
所以 5 封信装入写有不同地址和姓名的 5 个信封，全部装错的可能性有 44 种。通过本题可以收获到错位排列这一数学模型以及其递推公式的应用，在遇到类似元素不能对应到原来位置的排列问题时可以运用该方法求解。
【答案】：了解了错位排列问题，知道可以用递推公式 $D_n=(n - 1)(D_{n - 1}+D_{n - 2})$（$D_1 = 0$，$D_2 = 1$）来计算 $n$ 个元素全部错位排列的情况数，能运用此知识解决类似的装错信封、人员坐错位置等问题。

3.(2023·衢州)如图,在△ABC中,以点A为圆心,适当长为半径画弧,分别交AB,AC于点D,E.分别以点D,E为圆心,大于$\frac {1}{2}DE$长为半径画弧,交于∠BAC内一点F.连接AF并延长,交BC于点G.连接DG,EG.添加下列条件,不能使BG= CG成立的是(D)

A.AB= AC
B.AG⊥BC
C.∠DGB= ∠EGC
D.AG= AC

答案： 3.D

4.如图所示,三条公路两两相交于点A,B,C,现要修一个货物中转站,要求到三条公路距离相等,则可供选择的地址有(D)

A.一处
B.两处
C.三处
D.四处

答案： 4.D

5.(2023·阜新)如图,在矩形ABCD中,AB= 6,AD= 8.连接AC,在AC和AD上分别截取AE,AF,使AE= AF.分别以点E和点F为圆心,以大于$\frac {1}{2}EF$的长为半径作弧,两弧交于点G.作射线AG交CD于点H,则线段DH的长是______$\frac{8}{3}$.

答案： 5.$\frac{8}{3}$

6.如图,在Rt△ABC中,∠B= 90°,沿AD折叠,使点B落在斜边AC上.若AB= 3,BC= 4,则BD= ______.

6.$\frac{3}{2}$
填入答案后的题目为：
6.如图,在Rt△ABC中,∠B= 90°,沿AD折叠,使点B落在斜边AC上.若AB= 3,BC= 4,则BD= $\frac{3}{2}$.

答案： 6.$\frac{3}{2}$

7.如图所示,求作点P,使PA= PB,并使点P到∠MON的两边距离相等.
作法：点P为∠MON的平分线与线段AB垂直平分线的交点。

答案： 【解析】：
1. 作$\angle MON$的平分线$OC$：
根据角平分线的性质，角平分线上的点到角两边的距离相等。
2. 连接$AB$，作线段$AB$的垂直平分线$DE$：
因为垂直平分线上的点到线段两端的距离相等，所以$DE$上的点满足$PA = PB$。
3. 设$OC$与$DE$相交于点$P$：
点$P$既在$\angle MON$的平分线$OC$上，又在$AB$的垂直平分线$DE$上，所以点$P$即为所求作的点。
【答案】：点$P$为$\angle MON$的平分线与线段$AB$垂直平分线的交点。

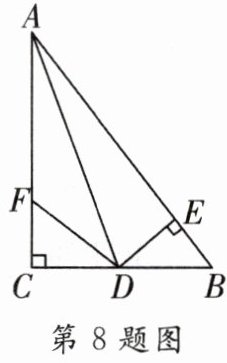
8.如图所示,在△ABC中,∠C= 90°,AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,且BD= DF.
(1)求证：CF= EB；
证明:∵AD是∠BAC的平分线,DE⊥AB,
　∠C=90°,
　∴DC=DE.
　在Rt△FCD和Rt△BED中,
　$\left\{\begin{array}{l} DC = DE, \\ DF = DB, \end{array}\right.$
　∴Rt△FCD≌Rt△BED(HL).
　∴CF=EB.
(2)试判断AB与AF,EB之间存在的数量关系.并说明理由.
解:在Rt△ACD和Rt△AED中,
　$\left\{\begin{array}{l} DC = DE, \\ AD = AD, \end{array}\right.$
　∴Rt△ACD≌Rt△AED(HL).
　∴AC=AE.
　∴AB=AE+BE=AF+FC+BE=AF+2BE.

答案： 8.
(1)证明:
∵AD是∠BAC的平分线,DE⊥AB,
　∠C=90°,
∴DC=DE.
　在Rt△FCD和Rt△BED中,
　$\left\{\begin{array}{l} DC = DE, \\ DF = DB, \end{array}\right.$
∴Rt△FCD≌Rt△BED(HL).
∴CF=EB.
(2)解:在Rt△ACD和Rt△AED中,
　$\left\{\begin{array}{l} DC = DE, \\ AD = AD, \end{array}\right.$
∴Rt△ACD≌Rt△AED(HL).
∴AC=AE.
∴AB=AE+BE=AF+FC+BE=AF+2BE.

9.如图所示,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF//BC交AB于E,交AC于F,过点O作OD⊥AC于D.
(1)若∠BAC= 110°,求∠BOC的度数；
(2)若BE= 4cm,CF= 2cm,求EF的长；
(3)若OD= 1cm,AE+AF= 7cm,求△AEF的面积.

答案：
9.解:
(1)∠BOC的度数为145°.
(2)
∵BO平分∠ABC,CO平分∠ACB,
∴∠ABO=∠OBC,∠ACO=∠OCB.
∵EF//BC,
∴∠EOB=∠OBC,∠FOC=∠OCB.
∴∠ABO=∠EOB,∠ACO=∠FOC;
∴BE=OE,OF=CF.
∵BE=4cm,CF=2cm,
∴OE=4cm,OF=2cm.
∴EF=OE+OF=4+2=6cm.
　即EF的长为6cm.
(3)如图所示,连接AO,过点O作OG⊥AB于G
　　　　
∵∠ABC与∠ACB的平分线交于点O,
∴AO平分∠BAC.
∵OG⊥AB,OD⊥AC,
∴OG=OD=1cm.
∴$S_{\triangle AEF} = S_{\triangle AOE} + S_{\triangle AOF}$
=$\frac{1}{2}OG \cdot AE + \frac{1}{2}OD \cdot AF$
=$\frac{1}{2}OG(AE + AF)$
=$\frac{1}{2} × 1 × 7 = \frac{7}{2}(cm^2)$.
∴△AEF的面积为$\frac{7}{2}cm^2$.