2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
直角三角形
趣味数学:
盲人分袜子的方法
有两位盲人,他们各自买了两双黑袜和两双白袜,八双袜子的布质、大小完全相同,而每双袜子都由一张商标纸连着.两位盲人不小心将八双袜子混在了一起.他们两人怎样才能取回各自的黑袜和白袜呢?
趣味数学:
盲人分袜子的方法
有两位盲人,他们各自买了两双黑袜和两双白袜,八双袜子的布质、大小完全相同,而每双袜子都由一张商标纸连着.两位盲人不小心将八双袜子混在了一起.他们两人怎样才能取回各自的黑袜和白袜呢?
答案:
【解析】:因为每双袜子都由一张商标纸连着,所以可以把每双袜子分开,两人各拿一只。这样对于每一双袜子,两位盲人都能拿到其中一只。由于总共是两双黑袜和两双白袜,按照这种分法,最后两人拿到的袜子组合起来就会是各自的两双黑袜和两双白袜。
【答案】:把每双袜子分开,两人各拿一只,最后两人都能取回各自的黑袜和白袜。
【答案】:把每双袜子分开,两人各拿一只,最后两人都能取回各自的黑袜和白袜。
5. (2020·玉林)下列命题中,其逆命题是真命题的是(
A.对顶角相等
B.两直线平行,同位角相等
C.全等三角形的对应角相等
D.正方形的四个角都相等
B
)A.对顶角相等
B.两直线平行,同位角相等
C.全等三角形的对应角相等
D.正方形的四个角都相等
答案:
B
6. 如图,已知在$\triangle ABC$中,$AB= AC$,$∠C= 30^{\circ }$,$AB⊥AD$,则下列关系式正确的为(
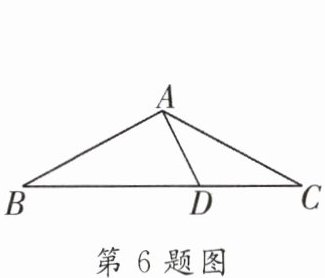
A.$BD= CD$
B.$BD= 2CD$
C.$BD= 3CD$
D.$BD= 4CD$
B
)
A.$BD= CD$
B.$BD= 2CD$
C.$BD= 3CD$
D.$BD= 4CD$
答案:
B
7. 将一副三角尺按如图所示的方式叠放在一起,若$AB= 14cm$,则阴影部分的面积是____
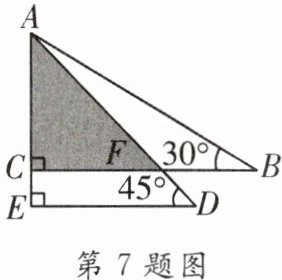
$\frac{49}{2}$
$cm^{2}$.
答案:
$\frac{49}{2}$
8. (2023·吉林)如图,在$Rt\triangle ABC$中,$∠C= 90^{\circ }$,$BC\lt AC$.点D,E分别在边AB,BC上,连接DE,将$\triangle BDE$沿DE折叠,点B的对应点为点$B'$.若点$B'$刚好落在边AC上,$∠CB'E= 30^{\circ }$,$CE= 3$,则BC的长为____
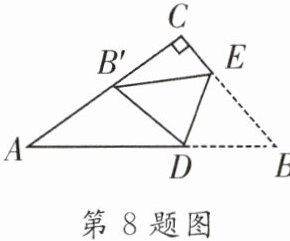
9
.
答案:
9
9. 如图,$∠AOP= ∠BOP= 15^{\circ }$,$PC// OA$,$PD⊥OA$,若$PC= 4$,则PD的长是____.
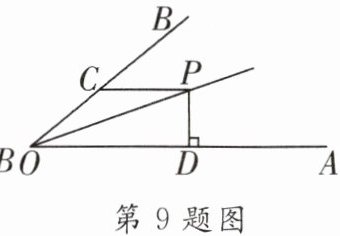

2
答案:
2
10. 如图所示,水池中离岸边D点1.5m的C处,直立长着一根芦苇,出水部分BC的长是0.5m,把芦苇拉到岸边,它的顶端B恰好会在D处,求水深AC.
解:设$AC = x$,则$AD = AB =$
由勾股定理得:
解得$x =$
即水深$AC$为
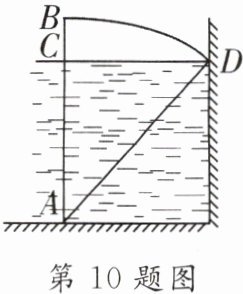
解:设$AC = x$,则$AD = AB =$
$x + 0.5$
,由勾股定理得:
$x^{2}+1.5^{2}=(x + 0.5)^{2}$
,解得$x =$
$2$
.即水深$AC$为
$2m$
.
答案:
解:设$AC = x$,则$AD = AB = x + 0.5$,
由勾股定理得:$x^{2}+1.5^{2}=(x + 0.5)^{2}$,
解得$x = 2$.
即水深$AC$为$2m$.
由勾股定理得:$x^{2}+1.5^{2}=(x + 0.5)^{2}$,
解得$x = 2$.
即水深$AC$为$2m$.
11. $\triangle ABC$的各边长分别为$a = m^{2}-n^{2}$,$b = 2mn$,$c = m^{2}+n^{2}$。
求证:$\triangle ABC$是直角三角形。
证明:$\because (m^{2}+n^{2})^{2}=m^{4}+2m^{2}n^{2}+n^{4}$,
$(m^{2}-n^{2})^{2}+(2mn)^{2}=m^{4}+n^{4}-2m^{2}n^{2}+4m^{2}n^{2}=m^{4}+2m^{2}n^{2}+n^{4}$,
$\therefore (m^{2}-n^{2})^{2}+(2mn)^{2}=(m^{2}+n^{2})^{2}$,
即$a^{2}+b^{2}=c^{2}$。
$\therefore \triangle ABC$为直角三角形。
求证:$\triangle ABC$是直角三角形。
证明:$\because (m^{2}+n^{2})^{2}=m^{4}+2m^{2}n^{2}+n^{4}$,
$(m^{2}-n^{2})^{2}+(2mn)^{2}=m^{4}+n^{4}-2m^{2}n^{2}+4m^{2}n^{2}=m^{4}+2m^{2}n^{2}+n^{4}$,
$\therefore (m^{2}-n^{2})^{2}+(2mn)^{2}=(m^{2}+n^{2})^{2}$,
即$a^{2}+b^{2}=c^{2}$。
$\therefore \triangle ABC$为直角三角形。
答案:
证明:$\because (m^{2}+n^{2})^{2}=m^{4}+2m^{2}n^{2}+n^{4}$,
$(m^{2}-n^{2})^{2}+(2mn)^{2}=m^{4}+n^{4}-2m^{2}n^{2}+4m^{2}n^{2}=m^{4}+2m^{2}n^{2}+n^{4}$,
$\therefore (m^{2}-n^{2})^{2}+(2mn)^{2}=(m^{2}+n^{2})^{2}$,
即$a^{2}+b^{2}=c^{2}$.
$\therefore \triangle ABC$为直角三角形.
$(m^{2}-n^{2})^{2}+(2mn)^{2}=m^{4}+n^{4}-2m^{2}n^{2}+4m^{2}n^{2}=m^{4}+2m^{2}n^{2}+n^{4}$,
$\therefore (m^{2}-n^{2})^{2}+(2mn)^{2}=(m^{2}+n^{2})^{2}$,
即$a^{2}+b^{2}=c^{2}$.
$\therefore \triangle ABC$为直角三角形.
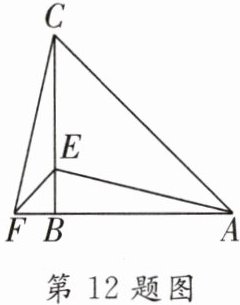
12. 如图所示,在$\triangle ABC$中,$AB= CB$,$∠ABC= 90^{\circ }$,F为AB延长线上一点,点E在BC上,且$AE= CF$.
(1) 求证:$Rt\triangle ABE≌Rt\triangle CBF$;
证明:在$Rt\triangle ABE$和$Rt\triangle CBF$中,
$\left\{\begin{array}{l} AB = CB,\\ AE = CF,\end{array}\right.$
$\therefore$
(2) 若$∠CAE= 30^{\circ }$,求$∠ACF$的度数.
解:$\because Rt\triangle ABE\cong Rt\triangle CBF$,$\angle CAE = 30^{\circ}$,
$\therefore$
$\therefore$
(1) 求证:$Rt\triangle ABE≌Rt\triangle CBF$;
证明:在$Rt\triangle ABE$和$Rt\triangle CBF$中,
$\left\{\begin{array}{l} AB = CB,\\ AE = CF,\end{array}\right.$
$\therefore$
$Rt\triangle ABE\cong Rt\triangle CBF(HL)$
.(2) 若$∠CAE= 30^{\circ }$,求$∠ACF$的度数.
解:$\because Rt\triangle ABE\cong Rt\triangle CBF$,$\angle CAE = 30^{\circ}$,
$\therefore$
$\angle BAE = \angle BCF = 15^{\circ}$
.$\therefore$
$\angle ACF = \angle ACB+\angle BCF = 15^{\circ}+45^{\circ}=60^{\circ}$
.
答案:
(1) 证明:在$Rt\triangle ABE$和$Rt\triangle CBF$中,
$\left\{\begin{array}{l} AB = CB,\\ AE = CF,\end{array}\right.$
$\therefore Rt\triangle ABE\cong Rt\triangle CBF(HL)$.
(2) 解:$\because Rt\triangle ABE\cong Rt\triangle CBF$,$\angle CAE = 30^{\circ}$,
$\therefore \angle BAE = \angle BCF = 15^{\circ}$.
$\therefore \angle ACF = \angle ACB+\angle BCF = 15^{\circ}+45^{\circ}=60^{\circ}$.
(1) 证明:在$Rt\triangle ABE$和$Rt\triangle CBF$中,
$\left\{\begin{array}{l} AB = CB,\\ AE = CF,\end{array}\right.$
$\therefore Rt\triangle ABE\cong Rt\triangle CBF(HL)$.
(2) 解:$\because Rt\triangle ABE\cong Rt\triangle CBF$,$\angle CAE = 30^{\circ}$,
$\therefore \angle BAE = \angle BCF = 15^{\circ}$.
$\therefore \angle ACF = \angle ACB+\angle BCF = 15^{\circ}+45^{\circ}=60^{\circ}$.
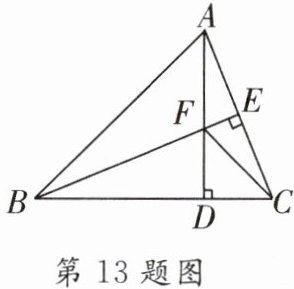
13. 如图所示,在$\triangle ABC$中,$AB= BC$,$BE⊥AC$于点E,$AD⊥BC$于点D,$∠BAD= 45^{\circ }$,AD与BE交于点F,连接CF.
(1)求证:$BF= 2AE$;
证明:$\because AD\perp BC$,$\angle BAD = 45^{\circ}$,
$\therefore \angle ABD = \angle BAD = 45^{\circ}$.$\therefore AD = BD$.
$\because AD\perp BC$,$BE\perp AC$,
$\therefore \angle CAD+\angle ACD = 90^{\circ}$,
$\angle CBE+\angle ACD = 90^{\circ}$.
$\therefore \angle CAD = \angle CBE$.
又$\because \angle CDA = \angle FDB = 90^{\circ}$,
$\therefore \triangle ADC\cong \triangle BDF$.
$\therefore AC = BF$.
$\because AB = BC$,$BE\perp AC$,
$\therefore AE = EC$,即$AC = 2AE$.$\therefore BF = 2AE$.
(2)若$CD= \sqrt {2}$,求AD的长.
$\because \triangle ADC\cong \triangle BDF$,$\therefore DF = CD =$
$\therefore$ 在$Rt\triangle CDF$中,$CF = \sqrt{DF^{2}+CD^{2}}=\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}} =$
$\because BE\perp AC$,$AE = EC$,$\therefore AF = FC =$
$\therefore AD = AF + DF =$
(1)求证:$BF= 2AE$;
证明:$\because AD\perp BC$,$\angle BAD = 45^{\circ}$,
$\therefore \angle ABD = \angle BAD = 45^{\circ}$.$\therefore AD = BD$.
$\because AD\perp BC$,$BE\perp AC$,
$\therefore \angle CAD+\angle ACD = 90^{\circ}$,
$\angle CBE+\angle ACD = 90^{\circ}$.
$\therefore \angle CAD = \angle CBE$.
又$\because \angle CDA = \angle FDB = 90^{\circ}$,
$\therefore \triangle ADC\cong \triangle BDF$.
$\therefore AC = BF$.
$\because AB = BC$,$BE\perp AC$,
$\therefore AE = EC$,即$AC = 2AE$.$\therefore BF = 2AE$.
(2)若$CD= \sqrt {2}$,求AD的长.
$\because \triangle ADC\cong \triangle BDF$,$\therefore DF = CD =$
$\sqrt{2}$
.$\therefore$ 在$Rt\triangle CDF$中,$CF = \sqrt{DF^{2}+CD^{2}}=\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}} =$
$2$
.$\because BE\perp AC$,$AE = EC$,$\therefore AF = FC =$
$2$
.$\therefore AD = AF + DF =$
$2+\sqrt{2}$
.
答案:
解:
(1) 证明:$\because AD\perp BC$,$\angle BAD = 45^{\circ}$,
$\therefore \angle ABD = \angle BAD = 45^{\circ}$.$\therefore AD = BD$.
$\because AD\perp BC$,$BE\perp AC$,
$\therefore \angle CAD+\angle ACD = 90^{\circ}$,
$\angle CBE+\angle ACD = 90^{\circ}$.
$\therefore \angle CAD = \angle CBE$.
又$\because \angle CDA = \angle FDB = 90^{\circ}$,
$\therefore \triangle ADC\cong \triangle BDF$.
$\therefore AC = BF$.
$\because AB = BC$,$BE\perp AC$,
$\therefore AE = EC$,即$AC = 2AE$.$\therefore BF = 2AE$.
(2) $\because \triangle ADC\cong \triangle BDF$,$\therefore DF = CD = \sqrt{2}$.
$\therefore$ 在$Rt\triangle CDF$中,$CF = \sqrt{DF^{2}+CD^{2}}=\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}} = 2$.
$\because BE\perp AC$,$AE = EC$,$\therefore AF = FC = 2$.
$\therefore AD = AF + DF = 2+\sqrt{2}$.
(1) 证明:$\because AD\perp BC$,$\angle BAD = 45^{\circ}$,
$\therefore \angle ABD = \angle BAD = 45^{\circ}$.$\therefore AD = BD$.
$\because AD\perp BC$,$BE\perp AC$,
$\therefore \angle CAD+\angle ACD = 90^{\circ}$,
$\angle CBE+\angle ACD = 90^{\circ}$.
$\therefore \angle CAD = \angle CBE$.
又$\because \angle CDA = \angle FDB = 90^{\circ}$,
$\therefore \triangle ADC\cong \triangle BDF$.
$\therefore AC = BF$.
$\because AB = BC$,$BE\perp AC$,
$\therefore AE = EC$,即$AC = 2AE$.$\therefore BF = 2AE$.
(2) $\because \triangle ADC\cong \triangle BDF$,$\therefore DF = CD = \sqrt{2}$.
$\therefore$ 在$Rt\triangle CDF$中,$CF = \sqrt{DF^{2}+CD^{2}}=\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}} = 2$.
$\because BE\perp AC$,$AE = EC$,$\therefore AF = FC = 2$.
$\therefore AD = AF + DF = 2+\sqrt{2}$.
查看更多完整答案,请扫码查看


