2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
如何分马
从前有一位老年人,在他临终时,三个儿子围在床前。他对儿子们说:“我有十七匹马留给你们三个人分。分马的时候,老大呢,出力最多,得总数的二分之一;老二嘛,得总数的三分之一;老三最小,你呀,就拿总数的九分之一。”勉强说完这几句,老人就去世了。三兄弟执行遗嘱时,一致认为这些马是父亲生前心爱之物,决不能将其中任何一匹劈成几块瓜分。但是遗嘱又要完全照办,如何是好呢?
从前有一位老年人,在他临终时,三个儿子围在床前。他对儿子们说:“我有十七匹马留给你们三个人分。分马的时候,老大呢,出力最多,得总数的二分之一;老二嘛,得总数的三分之一;老三最小,你呀,就拿总数的九分之一。”勉强说完这几句,老人就去世了。三兄弟执行遗嘱时,一致认为这些马是父亲生前心爱之物,决不能将其中任何一匹劈成几块瓜分。但是遗嘱又要完全照办,如何是好呢?
答案:
解:先借一匹马,此时马的总数为$17 + 1 = 18$匹。
老大分得:$18×\frac{1}{2}=9$匹;
老二分得:$18×\frac{1}{3}=6$匹;
老三分得:$18×\frac{1}{9}=2$匹;
三人共分得$9 + 6 + 2 = 17$匹,把借的那匹马还回去。
我的收获:在解决问题时,当直接按给定条件计算不方便时,可以通过巧妙地借数(或其他量)来辅助计算,最后再将借的数还回去,从而顺利解决问题。这种方法体现了数学思维的灵活性和创造性。
老大分得:$18×\frac{1}{2}=9$匹;
老二分得:$18×\frac{1}{3}=6$匹;
老三分得:$18×\frac{1}{9}=2$匹;
三人共分得$9 + 6 + 2 = 17$匹,把借的那匹马还回去。
我的收获:在解决问题时,当直接按给定条件计算不方便时,可以通过巧妙地借数(或其他量)来辅助计算,最后再将借的数还回去,从而顺利解决问题。这种方法体现了数学思维的灵活性和创造性。
5.已知等腰三角形中的一个内角为50°,则这个等腰三角形的顶角为(
A.50°
B.80°
C.50°或80°
D.50°或100°
C
)A.50°
B.80°
C.50°或80°
D.50°或100°
答案:
C
6.(2023·重庆)如图,在△ABC中,AB= AC,AD是BC边的中线,若AB= 5,BC= 6,则AD的长度为____

4
。
答案:
4
7.(黑龙江中考)如图所示,在△ABC中,AB= AC,点D在AC上,且BD= BC= AD,则∠A=
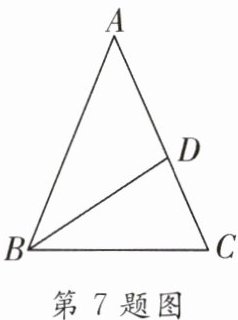
36
度。
答案:
36
8.(2023·江西)将含30°角的直角三角板和直尺按如图所示的方式放置,已知∠α= 60°,点B,C表示的刻度分别为1cm,3cm,则线段AB的长为____
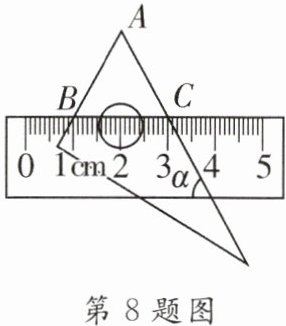
2
____cm。
答案:
2
9.(2022·云南)已知△ABC是等腰三角形。若∠A= 40°,则△ABC的顶角度数是
$40^{\circ}$或$100^{\circ}$
。
答案:
$40^{\circ}$或$100^{\circ}$
10.如图所示,锐角△ABC的两条高BD,CE相交于点O,且OB= OC.求证:△ABC是等腰三角形。
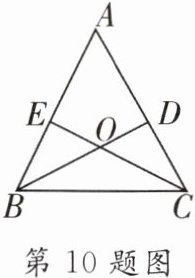
证明:

证明:
$\because OB = OC$,
$\therefore ∠OBC = ∠OCB$。
$\because BD⊥AC$,$CE⊥AB$,
$\therefore ∠BEC = ∠CDB = 90^{\circ}$。
$\because ∠BOE = ∠COD$,
$\therefore ∠EBO = ∠DCO$。
$\therefore ∠ABC = ∠ACB$。
$\therefore AB = AC$。
$\therefore △ABC$是等腰三角形。
$\therefore ∠OBC = ∠OCB$。
$\because BD⊥AC$,$CE⊥AB$,
$\therefore ∠BEC = ∠CDB = 90^{\circ}$。
$\because ∠BOE = ∠COD$,
$\therefore ∠EBO = ∠DCO$。
$\therefore ∠ABC = ∠ACB$。
$\therefore AB = AC$。
$\therefore △ABC$是等腰三角形。
答案:
证明:$\because OB = OC$,
$\therefore ∠OBC = ∠OCB$。
$\because BD⊥AC$,$CE⊥AB$,
$\therefore ∠BEC = ∠CDB = 90^{\circ}$。
$\because ∠BOE = ∠COD$,
$\therefore ∠EBO = ∠DCO$。
$\therefore ∠ABC = ∠ACB$。
$\therefore AB = AC$。
$\therefore △ABC$是等腰三角形。
$\therefore ∠OBC = ∠OCB$。
$\because BD⊥AC$,$CE⊥AB$,
$\therefore ∠BEC = ∠CDB = 90^{\circ}$。
$\because ∠BOE = ∠COD$,
$\therefore ∠EBO = ∠DCO$。
$\therefore ∠ABC = ∠ACB$。
$\therefore AB = AC$。
$\therefore △ABC$是等腰三角形。
11.(2024·重庆模拟)如图所示,在△ABC中,AB= AC,AD⊥BC于点D.
(1)若∠C= 42°,求∠BAD的度数;
解:
(2)若点E在边AB上,EF//AC交AD的延长线于点F.求证:AE= FE.
证明:

(1)若∠C= 42°,求∠BAD的度数;
解:
$\because AB = AC$,$AD⊥BC$于点$D$,$\therefore ∠BAD = ∠CAD$,$∠ADC = 90^{\circ}$。又$\because ∠C = 42^{\circ}$,$\therefore ∠BAD = ∠CAD = 90^{\circ} - 42^{\circ} = 48^{\circ}$。
(2)若点E在边AB上,EF//AC交AD的延长线于点F.求证:AE= FE.
证明:
$\because AB = AC$,$AD⊥BC$于点$D$,$\therefore ∠BAD = ∠CAD$。$\because EF// AC$,$\therefore ∠F = ∠CAD$。$\therefore ∠BAD = ∠F$。$\therefore AE = FE$。

答案:
解:
(1)$\because AB = AC$,$AD⊥BC$于点$D$,
$\therefore ∠BAD = ∠CAD$,$∠ADC = 90^{\circ}$。
又$\because ∠C = 42^{\circ}$,
$\therefore ∠BAD = ∠CAD = 90^{\circ} - 42^{\circ} = 48^{\circ}$。
(2)证明:$\because AB = AC$,$AD⊥BC$于点$D$,
$\therefore ∠BAD = ∠CAD$。
$\because EF// AC$,
$\therefore ∠F = ∠CAD$。
$\therefore ∠BAD = ∠F$。
$\therefore AE = FE$。
(1)$\because AB = AC$,$AD⊥BC$于点$D$,
$\therefore ∠BAD = ∠CAD$,$∠ADC = 90^{\circ}$。
又$\because ∠C = 42^{\circ}$,
$\therefore ∠BAD = ∠CAD = 90^{\circ} - 42^{\circ} = 48^{\circ}$。
(2)证明:$\because AB = AC$,$AD⊥BC$于点$D$,
$\therefore ∠BAD = ∠CAD$。
$\because EF// AC$,
$\therefore ∠F = ∠CAD$。
$\therefore ∠BAD = ∠F$。
$\therefore AE = FE$。
12.如图所示,在Rt△ABC中,∠ACB= 90°,∠B= 30°,AD平分∠CAB.
(1)求∠CAD的度数;
解:$\because$在$Rt△ABC$中,$∠ACB = 90^{\circ}$,$∠B = 30^{\circ}$,$\therefore ∠CAB = 60^{\circ}$。
又$\because AD$平分$∠CAB$,
$\therefore ∠CAD = \frac{1}{2}∠CAB =$
即$∠CAD =$
(2)延长AC至E,使EC= AC,求证:DA= DE.
证明:$\because ∠ACD + ∠ECD = 180^{\circ}$,
且$∠ACD = 90^{\circ}$,$\therefore ∠ECD = 90^{\circ}$。
$\therefore ∠ACD = ∠ECD$。
在$△ACD$与$△ECD$中,
$\because \left\{\begin{array}{l} AC = EC,\\ ∠ACD = ∠ECD,\\ CD = CD,\end{array}\right.$
$\therefore △ACD\cong △ECD(SAS)$。
$\therefore DA =$
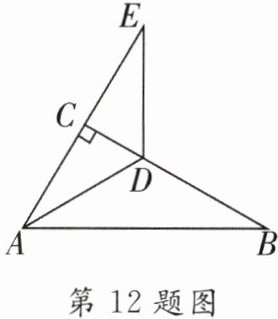
(1)求∠CAD的度数;
解:$\because$在$Rt△ABC$中,$∠ACB = 90^{\circ}$,$∠B = 30^{\circ}$,$\therefore ∠CAB = 60^{\circ}$。
又$\because AD$平分$∠CAB$,
$\therefore ∠CAD = \frac{1}{2}∠CAB =$
$30^{\circ}$
,即$∠CAD =$
$30^{\circ}$
。(2)延长AC至E,使EC= AC,求证:DA= DE.
证明:$\because ∠ACD + ∠ECD = 180^{\circ}$,
且$∠ACD = 90^{\circ}$,$\therefore ∠ECD = 90^{\circ}$。
$\therefore ∠ACD = ∠ECD$。
在$△ACD$与$△ECD$中,
$\because \left\{\begin{array}{l} AC = EC,\\ ∠ACD = ∠ECD,\\ CD = CD,\end{array}\right.$
$\therefore △ACD\cong △ECD(SAS)$。
$\therefore DA =$
$DE$
。
答案:
解:
(1)$\because$在$Rt△ABC$中,$∠ACB = 90^{\circ}$,$∠B = 30^{\circ}$,$\therefore ∠CAB = 60^{\circ}$。
又$\because AD$平分$∠CAB$,
$\therefore ∠CAD = \frac{1}{2}∠CAB = 30^{\circ}$,
即$∠CAD = 30^{\circ}$。
(2)证明:$\because ∠ACD + ∠ECD = 180^{\circ}$,
且$∠ACD = 90^{\circ}$,$\therefore ∠ECD = 90^{\circ}$。
$\therefore ∠ACD = ∠ECD$。
在$△ACD$与$△ECD$中,
$\because \left\{\begin{array}{l} AC = EC,\\ ∠ACD = ∠ECD,\\ CD = CD,\end{array}\right.$
$\therefore △ACD\cong △ECD(SAS)$。
$\therefore DA = DE$。
(1)$\because$在$Rt△ABC$中,$∠ACB = 90^{\circ}$,$∠B = 30^{\circ}$,$\therefore ∠CAB = 60^{\circ}$。
又$\because AD$平分$∠CAB$,
$\therefore ∠CAD = \frac{1}{2}∠CAB = 30^{\circ}$,
即$∠CAD = 30^{\circ}$。
(2)证明:$\because ∠ACD + ∠ECD = 180^{\circ}$,
且$∠ACD = 90^{\circ}$,$\therefore ∠ECD = 90^{\circ}$。
$\therefore ∠ACD = ∠ECD$。
在$△ACD$与$△ECD$中,
$\because \left\{\begin{array}{l} AC = EC,\\ ∠ACD = ∠ECD,\\ CD = CD,\end{array}\right.$
$\therefore △ACD\cong △ECD(SAS)$。
$\therefore DA = DE$。
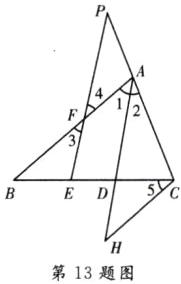
13.在△ABC中,AD平分∠BAC,E是BC上一点,BE= CD,EF//AD交AB于F点,交CA的延长线于P,CH//AB交AD的延长线于点H,
(1)求证:△APF是等腰三角形;
(2)猜想AB与PC的大小有什么关系?证明你的猜想。

(1)求证:△APF是等腰三角形;
(2)猜想AB与PC的大小有什么关系?证明你的猜想。

答案:
证明:
(1)如图所示。
$\because EF// AD$,
$\therefore ∠1 = ∠4$,$∠2 = ∠P$。
$\because AD$平分$∠BAC$,
$\therefore ∠1 = ∠2$。
$\therefore ∠4 = ∠P$。
$\therefore AF = AP$,
即$△APF$是等腰三角形。
(2)$AB = PC$。
理由如下:
$\because CH// AB$,
$\therefore ∠5 = ∠B$,$∠H = ∠1$。
$\because EF// AD$,
$\therefore ∠1 = ∠3$。
$\therefore ∠H = ∠3$。
在$△BEF$和$△CDH$中,
$\left\{\begin{array}{l} ∠5 = ∠B,\\ ∠H = ∠3,\\ BE = CD,\end{array}\right.$
$\therefore △BEF\cong △CDH(AAS)$,
$\therefore BF = CH$。
$\because AD$平分$∠BAC$,
$\therefore ∠1 = ∠2$。
$\therefore ∠2 = ∠H$。
$\therefore AC = CH$。
$\therefore AC = BF$。
$\because AB = AF + BF$,$PC = AP + AC$,
$\therefore AB = PC$。
证明:
(1)如图所示。
$\because EF// AD$,
$\therefore ∠1 = ∠4$,$∠2 = ∠P$。
$\because AD$平分$∠BAC$,
$\therefore ∠1 = ∠2$。
$\therefore ∠4 = ∠P$。
$\therefore AF = AP$,
即$△APF$是等腰三角形。

(2)$AB = PC$。
理由如下:
$\because CH// AB$,
$\therefore ∠5 = ∠B$,$∠H = ∠1$。
$\because EF// AD$,
$\therefore ∠1 = ∠3$。
$\therefore ∠H = ∠3$。
在$△BEF$和$△CDH$中,
$\left\{\begin{array}{l} ∠5 = ∠B,\\ ∠H = ∠3,\\ BE = CD,\end{array}\right.$
$\therefore △BEF\cong △CDH(AAS)$,
$\therefore BF = CH$。
$\because AD$平分$∠BAC$,
$\therefore ∠1 = ∠2$。
$\therefore ∠2 = ∠H$。
$\therefore AC = CH$。
$\therefore AC = BF$。
$\because AB = AF + BF$,$PC = AP + AC$,
$\therefore AB = PC$。
查看更多完整答案,请扫码查看


