《2025年轻松暑假复习加预习中国海洋大学出版社七年级数学鲁教版54制》

4. (2022·沈阳)不等式$2x+1＞3$的解集在数轴上表示正确的是(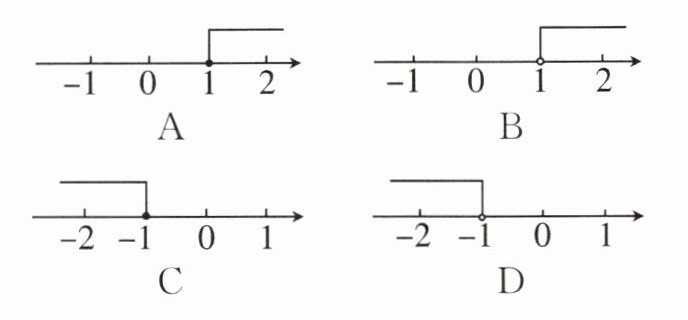B)

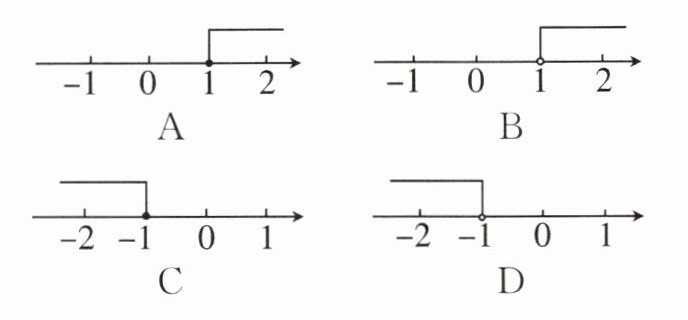
答案： 4. B

5. (2022·安徽)不等式$\frac {x-3}{2}≥1$的解集为__$x \geq 5$__.

答案： 5. $x \geq 5$

6. (湖北中考)若关于$x$,$y$的二元一次方程组$\left\{\begin{array}{l} x - 3y = 4m + 3\\ x + 5y = 5\end{array}\right.$的解满足$x + y\leq0$，则$m$的取值范围是____$m \leq -2$

答案： 6. $m \leq -2$

7. (湖南中考)若$a$为有理数,且$2 - a$的值大于1,则$a$的取值范围为____$a ＜ 1$

答案： 7. $a ＜ 1$

8. (2024·四川模拟)点$M(x-1,-3)$在第四象限,则$x$的取值范围是____$x ＞ 1$.

答案： 8. $x ＞ 1$

9. (2023·西宁)象征吉祥富贵的丁香花是西宁市市花. 为美化丁香大道,园林局准备购买某种规格的丁香花,若每棵6元,总费用不超过5000元,则最多可以购买____833棵.

答案： 9. 833

10. (1)(江苏中考)解不等式$\frac {4x-1}{3}-x＞1$,并在数轴上表示解集.
(2)(山东中考)已知关于$x$,$y的二元一次方程组\left\{\begin{array}{l} 2x-3y= 5,\\ x-2y= k\end{array} \right. 的解满足x＞y$,求$k$的取值范围.

答案：
10.
(1)解：$4x - 1 - 3x ＞ 3$，
$4x - 3x ＞ 3 + 1$，
$x ＞ 4$，
将不等式的解集表示在数轴上如图：

(2)解：$\begin{cases}2x - 3y = 5, &①\\x - 2y = k. &②\end{cases}$
① - ②得 $x - y = 5 - k$.
$\because x ＞ y$，
$\therefore x - y ＞ 0$.
$\therefore 5 - k ＞ 0$.
解得 $k ＜ 5$

11. 已知不等式$a(x-1)＞x+1-2a的解集是x＜-1$,请确定$a$的取值范围.

答案： 11. 解：$ax - a ＞ x + 1 - 2a$，
$ax - x ＞ 1 - 2a + a$，
$(a - 1)x ＞ 1 - a$，
由于不等式的解集是 $x ＜ -1$，所以 $a - 1 ＜ 0$，即 $a ＜ 1$.

12. 已知$x= 3是关于x的不等式3x-\frac {ax+2}{2}＞\frac {2x}{3}$的一个解,求$a$的取值范围.

答案： 12. 解：将 $x = 3$ 代入不等式得 $9 - \frac{3a + 2}{2} ＞ 2$. 解这个不等式得 $a ＜ 4$. $\therefore a$ 的取值范围为 $a ＜ 4$.

13. 某种商品的进价为800元,出售时标价为1200元. 后来由于该商品积压,商店准备打折出售,但要保持利润不低于5%,请你帮忙算一算,该商品至多可以打几折？

答案： 13. 解：设该商品可以打 $x$ 折.
由题意得 $1200 \cdot \frac{x}{10} - 800 \geq 800 × 5\%$，
解得 $x \geq 7$.
答：该商品至多可以打 7 折.

14. (辽宁中考)为响应“绿色生活,美丽家园”号召,某社区计划种植甲、乙两种花卉来美化小区环境. 若种植甲种花卉$2m^{2}$,乙种花卉$3m^{2}$,共需430元；种植甲种花卉$1m^{2}$,乙种花卉$2m^{2}$,共需260元.
(1)求：该社区种植甲种花卉$1m^{2}和种植乙种花卉1m^{2}$各需多少元？
(2)该社区准备种植两种花卉共$75m^{2}$且费用不超过6300元,那么社区最多能种植乙种花卉多少平方米？

答案： 14. 解：
(1)设该社区种植甲种花卉 $1m^2$ 需 $x$ 元，种植乙种花卉 $1m^2$ 需 $y$ 元.
依题意，得 $\begin{cases}2x + 3y = 430,\\x + 2y = 260.\end{cases}$
解得：$\begin{cases}x = 80,\\y = 90.\end{cases}$
答：该社区种植甲种花卉 $1m^2$ 需 80 元，种植乙种花卉 $1m^2$ 需 90 元.
(2)设该社区种植乙种花卉 $m m^2$，则种植甲种花卉 $(75 - m)m^2$，
依题意，得 $80(75 - m) + 90m \leq 6300$.
解得：$m \leq 30$.
答：该社区最多能种植乙种花卉 $30m^2$.