第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1 [2025江苏连云港调研]如图,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥的侧面(无重叠且无缝隙),则围成的圆锥底面圆的半径为(
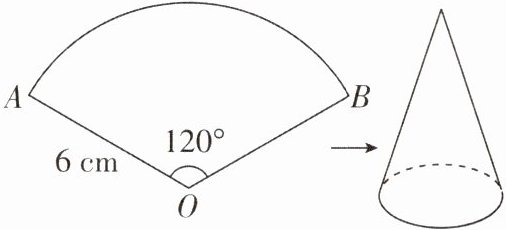
A.1cm
B.2cm
C.3cm
D.4cm
B
)
A.1cm
B.2cm
C.3cm
D.4cm
答案:
B 【解析】设围成的圆锥的底面圆的半径为r cm. 根据题意得 $2\pi r=\frac{120\pi × 6}{180}$,解得 $r=2$,即围成的圆锥的底面圆的半径为2 cm. 故选 B.
已知圆锥的底面半径为3,母线长为12,则其侧面展开扇形的圆心角的度数为
90
°。
答案:
90 【解析】设该圆锥侧面展开扇形的圆心角的度数为 $n^{\circ}$,则 $2\pi × 3=\frac{n\pi × 12}{180}$,解得 $n=90$,故答案为 90.
3 [2025江苏无锡期末]若圆锥的底面圆半径是1cm,它的侧面展开图的圆心角是直角,则该圆锥的高为
$\sqrt{15}$
cm。
答案:
$\sqrt{15}$ 【解析】设圆锥的母线长为 $l$ cm. 根据题意得 $2\pi \cdot 1=\frac{90\pi l}{180}$,解得 $l=4$,即圆锥的母线长为4 cm,
∴ 圆锥的高为 $\sqrt{4^{2}-1^{2}}=\sqrt{15}$ (cm),故答案为 $\sqrt{15}$.
∴ 圆锥的高为 $\sqrt{4^{2}-1^{2}}=\sqrt{15}$ (cm),故答案为 $\sqrt{15}$.
4 [2024江苏徐州调研]如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r= 2cm,扇形的圆心角θ= 120°,则该圆锥的母线长l为
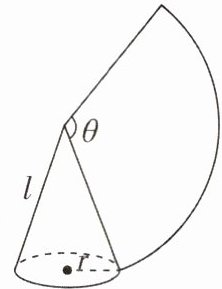
6
cm。
答案:
6 【解析】圆锥底面圆的周长为 $2\pi × 2=4\pi$ (cm),则 $\frac{120\pi × l}{180}=4\pi$,解得 $l=6$. 故答案为 6.
5 圆锥的高是4cm,其底面圆半径为3cm,则它的侧面展开图的面积为(
A.$12\pi cm^{2}$
B.$24\pi cm^{2}$
C.$15\pi cm^{2}$
D.$30\pi cm^{2}$
C
)A.$12\pi cm^{2}$
B.$24\pi cm^{2}$
C.$15\pi cm^{2}$
D.$30\pi cm^{2}$
答案:
C 【解析】这个圆锥的母线长为 $\sqrt{3^{2}+4^{2}}=5$ (cm),所以这个圆锥的侧面积为 $\frac{1}{2}× 2\pi × 3× 5=15\pi$ ($cm^{2}$). 故选 C.
6 设圆锥的底面圆半径为r,圆锥的母线长为l,且满足2r + l = 6,则这样的圆锥的侧面积(
A.有最大值$\frac{9}{4}\pi$
B.有最小值$\frac{9}{4}\pi$
C.有最大值$\frac{9}{2}\pi$
D.有最小值$\frac{9}{2}\pi$
C
)A.有最大值$\frac{9}{4}\pi$
B.有最小值$\frac{9}{4}\pi$
C.有最大值$\frac{9}{2}\pi$
D.有最小值$\frac{9}{2}\pi$
答案:
C 【解析】
∵ $2r+l=6$,
∴ $l=6-2r$,
∴ 圆锥的侧面积为 $\pi rl=\pi r(6-2r)=-2\pi (r^{2}-3r)=-2\pi \left[(r-\frac{3}{2})^{2}-\frac{9}{4}\right]=-2\pi (r-\frac{3}{2})^{2}+\frac{9}{2}\pi$,
∴ 当 $r=\frac{3}{2}$ 时,圆锥的侧面积有最大值,为 $\frac{9}{2}\pi$. 故选 C.
∵ $2r+l=6$,
∴ $l=6-2r$,
∴ 圆锥的侧面积为 $\pi rl=\pi r(6-2r)=-2\pi (r^{2}-3r)=-2\pi \left[(r-\frac{3}{2})^{2}-\frac{9}{4}\right]=-2\pi (r-\frac{3}{2})^{2}+\frac{9}{2}\pi$,
∴ 当 $r=\frac{3}{2}$ 时,圆锥的侧面积有最大值,为 $\frac{9}{2}\pi$. 故选 C.
7 [2024江苏南京栖霞区调研]如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为$20\pi cm$,侧面积为$240\pi cm^{2}$,则这个扇形的圆心角的度数是
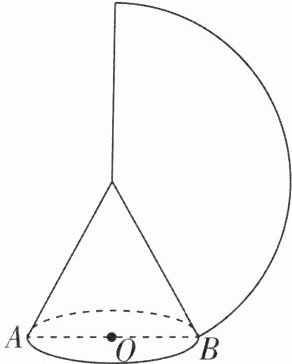
150
度。
答案:
150 【解析】设圆锥的母线长为 $l$ cm,扇形的圆心角为 $n^{\circ}$. 由题意得 $\frac{1}{2}× 20\pi × l=240\pi$,解得 $l=24$.
∵ 圆锥的底面圆周长为 $20\pi$ cm,
∴ 圆锥的侧面展开图扇形的弧长为 $20\pi$ cm,
∴ $\frac{n\pi × 24}{180}=20\pi$,解得 $n=150$,即扇形的圆心角为 $150^{\circ}$,故答案为 150.
∵ 圆锥的底面圆周长为 $20\pi$ cm,
∴ 圆锥的侧面展开图扇形的弧长为 $20\pi$ cm,
∴ $\frac{n\pi × 24}{180}=20\pi$,解得 $n=150$,即扇形的圆心角为 $150^{\circ}$,故答案为 150.
(1)△ABC外接圆的圆心P的坐标是
(2)求圆心P到弦AC的距离;
(3)以BC所在直线为旋转轴,将△ABC旋转一周,求所得几何体的表面积。
(5,2)
;(2)求圆心P到弦AC的距离;
令 AC 的中点为 D,如图. 根据中点公式,可得 AC 的中点 D 的坐标为(2,3),∴ 点 P 到弦 AC 的距离为 $\sqrt{(5-2)^{2}+(2-3)^{2}}=\sqrt{10}$
(3)以BC所在直线为旋转轴,将△ABC旋转一周,求所得几何体的表面积。
旋转后的几何体为底面半径为 2,高为 6 的圆锥减去底面半径为 2,高为 2 的圆锥. ∵ $AC=\sqrt{(3-1)^{2}+6^{2}}=2\sqrt{10}$,$AB=\sqrt{(3-1)^{2}+(6-4)^{2}}=2\sqrt{2}$,∴ 所得几何体表面积为 $2\sqrt{10}× 2\pi +2\sqrt{2}× 2\pi =4\sqrt{10}\pi +4\sqrt{2}\pi$
答案:
(1)(5,2);
(2)令 AC 的中点为 D,如图. 根据中点公式,可得 AC 的中点 D 的坐标为(2,3),
∴ 点 P 到弦 AC 的距离为 $\sqrt{(5-2)^{2}+(2-3)^{2}}=\sqrt{10}$;
(3)旋转后的几何体为底面半径为 2,高为 6 的圆锥减去底面半径为 2,高为 2 的圆锥.
∵ $AC=\sqrt{(3-1)^{2}+6^{2}}=2\sqrt{10}$,$AB=\sqrt{(3-1)^{2}+(6-4)^{2}}=2\sqrt{2}$,
∴ 所得几何体表面积为 $2\sqrt{10}× 2\pi +2\sqrt{2}× 2\pi =4\sqrt{10}\pi +4\sqrt{2}\pi$.
(1)(5,2);
(2)令 AC 的中点为 D,如图. 根据中点公式,可得 AC 的中点 D 的坐标为(2,3),
∴ 点 P 到弦 AC 的距离为 $\sqrt{(5-2)^{2}+(2-3)^{2}}=\sqrt{10}$;
(3)旋转后的几何体为底面半径为 2,高为 6 的圆锥减去底面半径为 2,高为 2 的圆锥.
∵ $AC=\sqrt{(3-1)^{2}+6^{2}}=2\sqrt{10}$,$AB=\sqrt{(3-1)^{2}+(6-4)^{2}}=2\sqrt{2}$,
∴ 所得几何体表面积为 $2\sqrt{10}× 2\pi +2\sqrt{2}× 2\pi =4\sqrt{10}\pi +4\sqrt{2}\pi$.
9 如图,矩形纸片ABCD中,AD= 9cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为______
6 cm
。
答案:
6 cm 【解析】设圆锥的底面圆的半径为 $r$ cm,则 $DE=2r$ cm,$AE=AB=(9-2r)$ cm. 根据题意得 $\frac{90\pi × (9-2r)}{180}=2\pi r$,解得 $r=\frac{3}{2}$,所以 $AB=9-2r=9-2× \frac{3}{2}=6$ (cm).
查看更多完整答案,请扫码查看


