《2025年初中必刷题九年级数学上册苏科版》

1 [2025 江苏连云港期中,中]如图, $\odot O$ 的直径 $AB$ 垂直于弦 $CD$, 垂足为 $E$, $\angle A= 30^{\circ}$, 半径为 2, 则弦 $CD$ 的长为 (B)

A.2
B.$2 \sqrt{3}$
C.$\sqrt{3}$
D.4

答案： B [解析]
∵∠A=30°,
∴∠BOC=2∠A=60°.
∵⊙O的直径AB垂直于弦CD,垂足为E,半径为2,
∴OC=2,CD=2CE,∠OEC=90°,
∴∠OCE=30°,
∴OE= $\frac{1}{2}$OC=1,
∴CE= $\sqrt{OC^2-OE^2}$=$\sqrt{3}$,
∴CD=2$\sqrt{3}$.故选B.

2 [2024 河南漯河质检,中]如图,一座石桥的主桥拱是圆弧形,某时刻测得水面宽度 $AB$ 为 6 米,拱高 $CD$ (弧的中点到水面的距离) 为 1 米,若水面下降 1 米,则此时水面的宽度为 ( )


A.5 米
B.6 米
C.7 米
D.8 米

答案：
D [解析]如图,设桥拱所在圆的圆心为O,连接OC,OA,OB,则O,C,D三点共线.由题意可得，

D为弧AB的中点,
∴∠AOD=∠BOD.
∵OA=OB,
∴OD⊥AB,AC=BC.设OD=r米,则OC=OD - CD=(r - 1)米.在Rt△AOC中,OA²=OC²+AC²,AC= $\frac{1}{2}$AB=3米,
∴r²=(r - 1)²+9,解得r=5,
∴主桥拱所在圆的半径为5米,OC=4米.设下降后的水面为EF,EF交OC于点G,连接OE,易得EG=FG.
∵水面下降1米,
∴OG=OC - 1=4 - 1=3(米),则EG= $\sqrt{OE^2-OG^2}$=$\sqrt{5^2-3^2}$=4(米),
∴EF=2EG=8米,即此时水面的宽度为8米.故选D.

3 [中]如图,四边形 $BCDE$ 内接于 $\odot O$, $AB$ 是 $\odot O$ 的直径,满足 $AB \perp CD$ 于点 $F$, 连接 $AE$, $BD$. 若 $\angle ABC= \angle DBE$, $CF= 2AF= 4$, 则点 $E$ 到线段 $AB$ 的距离为______.

答案：
$\frac{24}{5}$ [解析]如图,连接OC,过点E作ER⊥AB于点R.设OA=OC=r.
∵AB⊥CD,AB是直径,
∴CF=DF=4,$\widehat{AC}$=$\widehat{AD}$.在Rt△OCF中,OC²=CF²+OF²,
∴r²=4²+(r - 2)²,
∴r=5,

∴AB=10.
∵∠ABC=∠DBE,
∴$\widehat{AC}$=$\widehat{DE}$=$\widehat{AD}$,
∴$\widehat{CD}$=$\widehat{AE}$,
∴CD=AE=8.
∵AB是直径,
∴∠AEB=90°,
∴BE= $\sqrt{AB^2-AE^2}$=$\sqrt{10^2-8^2}$=6.
∵ER⊥AB,
∴S△ABE= $\frac{1}{2}$AB·ER= $\frac{1}{2}$AE·BE,
∴ER= $\frac{24}{5}$,
∴点E到线段AB的距离为$\frac{24}{5}$.故答案为$\frac{24}{5}$.

4 [2024 江西南昌调研,较难]如图, $AB$ 是 $\odot O$ 的弦, 以 $AB$ 为边作等腰三角形 $ABC$, $\angle C= 100^{\circ}$, 若 $\odot O$ 的半径为 2 cm, 弦 $AB$ 的长为 $2 \sqrt{3} \mathrm{~cm}$, 点 $D$ 在 $\odot O$ 上, 若 $\angle D A C= \frac{1}{2} \angle B A C$, 则 $\angle D B A= $______ $^{\circ}$.

答案：
60或100或40 [解析]如图
(1)，过点O作OE⊥AB于E,连接OA,OB,则AE=BE= $\frac{1}{2}$AB=$\sqrt{3}$.
∵OA=OB=2,
∴由勾股定理得OE=1,
∴OE= $\frac{1}{2}$OA,
∴∠OAE=30°,
∴∠AOE=60°,同理可得∠BOE=60°,
∴∠AOB=120°.
∵△ABC是等腰三角形,∠C=100°,
∴∠BAC=∠ABC= $\frac{1}{2}$(180° - 100°)=40°,
∴∠DAC= $\frac{1}{2}$∠BAC=20°.①如图
(1),当点C在⊙O内,AD在AC的下方时,
∵∠AOB=120°,
∴∠D=60°.
∵∠BAD=∠BAC+∠DAC=40°+20°=60°,
∴∠DBA=180° - ∠D - ∠BAD=180° - 60° - 60°=60°.②如图
(2)，当点C在⊙O内,AD在∠BAC内部时,同①可得∠D=60°.
∵∠BAD=∠BAC - ∠CAD=20°,
∴∠DBA=180° - ∠D - ∠BAD=180° - 60° - 20°=100°.③如图
(3),当点C在⊙O的外部,AD在∠BAC内部时,同②可得∠BAD=20°.
∵$\widehat{AB}$的度数为120°,
∴$\widehat{AMB}$的度数为240°,
∴∠BDA=120°,
∴∠DBA=180° - ∠BDA - ∠BAD=180° - 120° - 20°=40°.综上,∠DBA=60°或100°或40°.故答案为60或100或40.

5 [较难]如图, 以 $AB$ 为直径的 $\odot O$ 经过 $\triangle ABC$ 的顶点 $C$, $AE$, $BE$ 分别平分 $\angle BAC$ 和 $\angle ABC$, $AE$ 的延长线交 $\odot O$ 于点 $D$, 连接 $BD$.
(1) 判断 $\triangle BDE$ 的形状, 并证明你的结论;
(2) 若 $AB= 10$, $BE= 2 \sqrt{10}$, 求 $BC$ 的长.

答案：
[解]
(1)△BDE为等腰直角三角形.证明:
∵AE平分∠BAC,BE平分∠ABC,
∴∠BAE=∠CAD=∠CBD,∠ABE=∠EBC.
∵∠BED=∠BAE+∠ABE,∠DBE=∠DBC+∠CBE,
∴∠BED=∠DBE,
∴BD=ED.
∵AB为直径,
∴∠ADB=90°,
∴△BDE是等腰直角三角形.
(2)如图,连接OC,CD,OD,OD交BC于点F.
∵∠DBC=∠CAD=∠BAD=∠BCD,

∴BD=DC.
∵OB=OC,
∴OD垂直平分BC.
∵△BDE是等腰直角三角形,BE=2$\sqrt{10}$,
∴BD=2$\sqrt{5}$.
∵AB=10,
∴OB=OD=5.设OF=t,则DF=5 - t.在Rt△BOF和Rt△BDF中,5² - t²=(2$\sqrt{5}$)² - (5 - t)²,解得t=3,
∴BF=4,
∴BC=8.

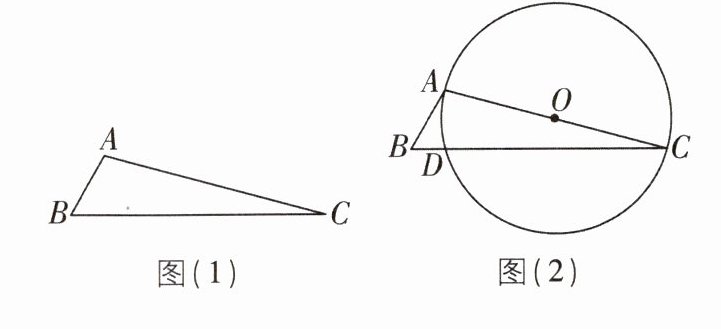
6 新考法 [2024 江苏苏州质检,较难]我们给出定义:如果三角形存在两个内角 $\alpha$ 与 $\beta$ 满足 $2 a+\beta=90^{\circ}$, 那么我们称这样的三角形为“准互余三角形”. 已知 $\triangle ABC$ 为“准互余三角形”, 并且 $\angle A＞\angle B＞\angle C$.
(1) 如图(1), 若 $\angle B= 60^{\circ}$ 且 $AB= \sqrt{3}$, 求边 $BC$ 的长;
(2) 如图(2), $\angle B＞45^{\circ}$, 以边 $AC$ 为直径作 $\odot O$, 交 $BC$ 于点 $D$, 若 $BD= 2$, $BC= 7$, 试求 $\odot O$ 的面积.

答案：
[解]
(1)
∵∠BAC＞∠B＞∠ACB,△ABC为“准互余三角形”,
∴2∠ACB+∠B=90°,即2∠ACB+60°=90°,
∴∠ACB=15°.过A点作AH⊥BC于H点,过C点作CD⊥AB,交BA的延长线于D点,如图
(1).在Rt△ABH中,
∵∠BAH=90° - ∠B=30°,
∴BH= $\frac{1}{2}$AB= $\frac{\sqrt{3}}{2}$,
∴AH= $\frac{3}{2}$.
∵∠BCD=90° - ∠B=30°,
∴CA平分∠BCD,
∴AD=AH= $\frac{3}{2}$,
∴BD=$\sqrt{3}$+ $\frac{3}{2}$.在Rt△BCD中,
∵∠BCD=30°,
∴BC=2BD=2$\sqrt{3}$+3.

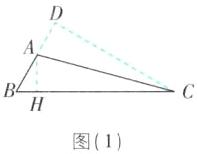
(2)延长BA交⊙O于E点,连接CE,AD,如图
(2).
∵AC为直径,
∴∠AEC=∠ADC=90°.
∵∠B＞45°,△ABC为“准互余三角形”,∠BAC＞∠B＞∠C,
∴2∠ACB+∠B=90°.
∵∠B+∠BCE=90°,
∴∠ACB=∠ACE,即CA平分∠BCE,
∴AE=AD.
∵AC=AC,
∴△ACD≌△ACE(AAS),CE=CD=BC - BD=5.在Rt△BCE中,BE= $\sqrt{BC^2-CE^2}$=$\sqrt{7^2-5^2}$=2$\sqrt{6}$.设AE=x,则AB=2$\sqrt{6}$ - x,AD=x.在Rt△ABD中,
∵BD²+AD²=AB²,
∴2²+x²=(2$\sqrt{6}$ - x)²,解得x= $\frac{5\sqrt{6}}{6}$.在Rt△ACD中,AC²=5²+($\frac{5\sqrt{6}}{6}$)²= $\frac{175}{6}$,
∴⊙O的面积为π× $\frac{1}{4}$AC²= $\frac{175}{24}$π.