《2025年初中必刷题九年级数学上册苏科版》

1[2025江苏苏州期中]将代数式$x^{2}+6x+2化成(x+p)^{2}+q$的形式为(B)
A.$(x-3)^{2}+11$
B.$(x+3)^{2}-7$
C.$(x+3)^{2}-11$
D.$(x+2)^{2}+4$

答案： B 【解析】$x^{2}+6x+2=x^{2}+6x+3^{2}-3^{2}+2=(x+3)^{2}-7$. 故选 B.

其中正确的结论是②④.

答案： ②④ 【解析】
① $\because x^{2}+ax+10=(x-3)^{2}+1=x^{2}-6x+10$, $\therefore a=-6$,故原结论错误
② $\because x^{2}+4y^{2}=12$,$xy=1$,$\therefore x^{2}+4xy+4y^{2}=12+4=16$,$\therefore (x+2y)^{2}=16$,则$x+2y=\pm 4$,故原结论正确
③ $\because a^{2}+b^{2}+2c^{2}=2bc-2ac$,$\therefore a^{2}+2ac+c^{2}+b^{2}-2bc+c^{2}=0$,$\therefore (a+c)^{2}+(b-c)^{2}=0$,$\therefore a+c=0$,$b-c=0$,$\therefore a+b=0$,即$a+b$的值是0,故原结论错误
④ $\because (m+\sqrt{3}n)^{2}=m^{2}+3n^{2}+2\sqrt{3}mn=a+4\sqrt{3}$, $\therefore 2mn=4$,$a=m^{2}+3n^{2}$,$\therefore mn=2$. $\because m,n$均为正整数,$\therefore m=1$,$n=2$或$m=2$,$n=1$. 当$m=1$,$n=2$时,$a=1+12=13$;当$m=2$,$n=1$时,$a=4+3=7$. 故$a$的值为13或7,故原结论正确

3[2025江苏连云港调研]用配方法解一元二次方程$x^{2}-2x-2024= 0$,将它转化为$(x+a)^{2}= b$的形式,则$a^{b}$的值为(C)
A.-2024
B.2024
C.-1
D.1

答案： C 【解析】$\because x^{2}-2x-2024=0$,$\therefore x^{2}-2x=2024$,$\therefore x^{2}-2x+1=2024+1$,$\therefore (x-1)^{2}=2025$,$\therefore a=-1$,$b=2025$,$\therefore a^{b}=(-1)^{2025}=-1$. 故选 C.

4[2025江苏南京期中]小明在计算正数a的平方时,误算成a与2的积,求得的答案比正确答案小1,则a的值为(C)
A.$\sqrt {2}-1$
B.$-\sqrt {2}+1$
C.$\sqrt {2}+1$
D.1或$\sqrt {2}+1$

答案： C 【解析】由题意得$a^{2}-2a=1$,配方得$(a-1)^{2}=2$,$\therefore a-1=\pm \sqrt{2}$,$\therefore a_{1}=\sqrt{2}+1$,$a_{2}=-\sqrt{2}+1$(舍去),$\therefore a$的值为$\sqrt{2}+1$. 故选 C.
易错警示
方程的左右两边都可以直接开平方,在解方程时需注意:两个数的平方相等,那么这两个数相等或互为相反数. 本题等号左右两边开平方后的两个代数式相等或互为相反数,不要漏解.
易错警示
移项是解方程的关键步骤,移项时要注意变号,否则会导致解题错误.

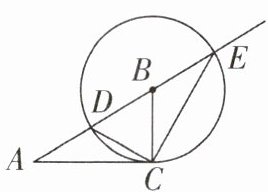
5新考法欧几里得的《几何原本》中记载了形如$x^{2}-2bx+4c^{2}= 0(b＞2c＞0)$的方程的根的图形解法:如图,画$Rt△ABC$,使$∠ACB= 90^{\circ },AC= 2c,AB= b$,以B为圆心,BC长为半径画圆,交射线AB于点D,E,则该方程较大的根是(D)


A.CE的长度
B.CD的长度
C.DE的长度
D.AE的长度

答案： D 【解析】$\because x^{2}-2bx+4c^{2}=0$,$\therefore x^{2}-2bx=-4c^{2}$,$\therefore x^{2}-2bx+b^{2}=b^{2}-4c^{2}$,即$(x-b)^{2}=b^{2}-4c^{2}$,$\therefore x-b=\pm \sqrt{b^{2}-4c^{2}}$,$\therefore x_{1}=b+\sqrt{b^{2}-4c^{2}}$,$x_{2}=b-\sqrt{b^{2}-4c^{2}}$. 在$\text{Rt}\triangle ABC$中,$\angle ACB=90^{\circ}$,$AC=2c$,$AB=b$,$\therefore BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{b^{2}-4c^{2}}$,$\therefore$方程较大的根为$AB+BC=AB+BE=AE$的长度,故选 D.

6已知方程$x^{2}-6x+4= □$,等号右侧的数字印刷不清.若可以将其配方成$(x-p)^{2}= 7$的形式,则印刷不清的数字是2.

答案： 2 【解析】设印刷不清的数字是$a$. $\because (x-p)^{2}=7$,$\therefore x^{2}-2px+p^{2}=7$,$\therefore x^{2}-2px=7-p^{2}$,$\therefore x^{2}-2px+4=11-p^{2}$. $\because$方程$x^{2}-6x+4=□$可以配方成$(x-p)^{2}=7$的形式,$\therefore -2p=-6$,$a=11-p^{2}$,$\therefore p=3$,$\therefore a=11-3^{2}=2$,即印刷不清的数字是2,故答案为2.

7[2024江苏常州期中]已知$x^{2}-3x+5= (x-2)^{2}+a(x-2)+b$,则$a+b= $4.

答案： 4 【解析】$x^{2}-3x+5=(x-2)^{2}+a(x-2)+b$,则$(x-2)^{2}+(x-2)+3=(x-2)^{2}+a(x-2)+b$,故$a=1$,$b=3$,则$a+b=4$. 故答案为4.

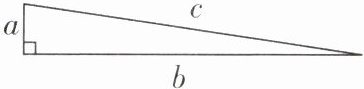
8[2025江苏南通调研]如图,直角三角形的两条直角边长分别为a,b,且a,b恰为一元二次方程$x^{2}-6x+4= 0$的两个实数根,则斜边c的长为$2\sqrt{7}$.

答案： $2\sqrt{7}$ 【解析】$\because x^{2}-6x+4=0$,$\therefore (x-3)^{2}-5=0$,解得$x_{1}=3-\sqrt{5}$,$x_{2}=3+\sqrt{5}$,$\therefore$斜边$c$的长为$\sqrt{(3-\sqrt{5})^{2}+(3+\sqrt{5})^{2}}=2\sqrt{7}$,故答案为$2\sqrt{7}$.

9用配方法解下列方程:
(1)$x^{2}+4x-3= 0$.
(2)$x^{2}-8x+13= 0$.

答案： 【解】
(1)移项,得$x^{2}+4x=3$. 配方,得$x^{2}+4x+4=3+4$,即$(x+2)^{2}=7$. 开方,得$x+2=\pm \sqrt{7}$,$\therefore x_{1}=\sqrt{7}-2$,$x_{2}=-\sqrt{7}-2$.
(2)移项,得$x^{2}-8x=-13$. 配方,得$x^{2}-8x+16=-13+16$,即$(x-4)^{2}=3$. 开方,得$x-4=\pm \sqrt{3}$,$\therefore x_{1}=\sqrt{3}+4$,$x_{2}=-\sqrt{3}+4$.

(1)小明的解答过程是从第一步开始出错的.
(2)用配方法写出此题正确的解答过程.
【解】$\because x^{2}-x-\frac{1}{2}=0$,$\therefore x^{2}-x=\frac{1}{2}$, $\therefore x^{2}-x+\frac{1}{4}=\frac{1}{2}+\frac{1}{4}$,即$\left(x-\frac{1}{2}\right)^{2}=\frac{3}{4}$, 则$x-\frac{1}{2}=\pm \frac{\sqrt{3}}{2}$,$\therefore x_{1}=\frac{1+\sqrt{3}}{2}$,$x_{2}=\frac{1-\sqrt{3}}{2}$.

答案： 【解】
(1)小明的解答过程是从第一步开始出错的,故答案为一.
(2)$\because x^{2}-x-\frac{1}{2}=0$,$\therefore x^{2}-x=\frac{1}{2}$, $\therefore x^{2}-x+\frac{1}{4}=\frac{1}{2}+\frac{1}{4}$,即$\left(x-\frac{1}{2}\right)^{2}=\frac{3}{4}$, 则$x-\frac{1}{2}=\pm \frac{\sqrt{3}}{2}$,$\therefore x_{1}=\frac{1+\sqrt{3}}{2}$,$x_{2}=\frac{1-\sqrt{3}}{2}$.