《2025年初中必刷题九年级数学上册苏科版》

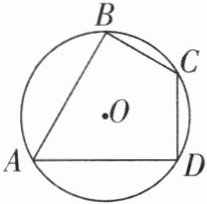
1[中]如图,四边形ABCD是$\odot O$的内接四边形,$∠B= 90^{\circ },∠A= 60^{\circ },AB= 3,CD= 2$,则AD的长为( )

A.$3\sqrt {3}-4$
B.$2\sqrt {3}$
C.$6-2\sqrt {3}$
D.3

答案：
C 【解析】如图，延长 AB，DC 交于点 E。
∵ 四边形 ABCD 是$\odot O$的内接四边形，$\therefore ∠ABC + ∠D = 180^{\circ}$。$\because ∠ABC = 90^{\circ}$，$\therefore ∠D = 90^{\circ}$，$∠EBC = 90^{\circ}$。$\because ∠A = 60^{\circ}$，$\therefore ∠E = 30^{\circ}$，$\therefore EC = 2BC$，$AE = 2AD$。设$BC = x$，则$EC = 2x$，$BE = \sqrt{3}x$。$\because AB = 3$，$CD = 2$，$\therefore AE = 3 + \sqrt{3}x$，$DE = 2 + 2x$，$\therefore AD = \frac{1}{2}AE = \frac{3 + \sqrt{3}x}{2}$。
∵ 由勾股定理易得$DE = \sqrt{3}AD$，$\therefore 2 + 2x = \sqrt{3}×\frac{3 + \sqrt{3}x}{2}$，解得$x = 3\sqrt{3}-4$，$\therefore AD = \frac{3 + \sqrt{3}×(3\sqrt{3}-4)}{2}= 6 - 2\sqrt{3}$，故选 C。

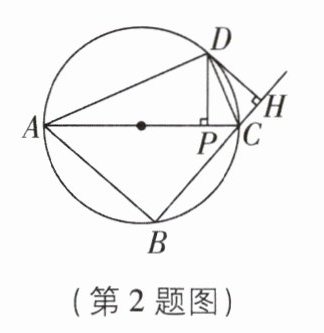
2构造同弧的圆周角[2025浙江杭州质检,中]如图,圆内接$\triangle ABC的外角∠ACH$的平分线与圆交于点D,$DP⊥AC$,垂足为P,$DH⊥BH$,垂足为H.有下列结论:①$\widehat {AD}= \widehat {BD}$;②$AP= BH$;③$\widehat {AB}= \widehat {BC}$.其中一定成立的结论有( )


A.1个
B.2个
C.3个
D.0个

答案：
B 【解析】连接 BD，如图。
∵ CD 平分$∠ACH$，$DP⊥AC$，$DH⊥BH$，$\therefore DP = DH$。
∵$∠DAP$和$∠DBH$是$\widehat{CD}$所对的圆周角，$\therefore ∠DAP = ∠DBH$。在$△ADP$和$△BDH$中，$\begin{cases}∠DAP = ∠DBH\\∠APD = ∠BHD = 90^{\circ}\\DP = DH\end{cases}$，$\therefore △ADP\cong △BDH(AAS)$，$\therefore AD = DB$，$AP = BH$，$\therefore \widehat{AD}=\widehat{BD}$，故①②成立。当且仅当$AB = BC$时，$\widehat{AB}=\widehat{BC}$，故③不一定成立。综上所述，一定成立的结论有 2 个，故选 B。

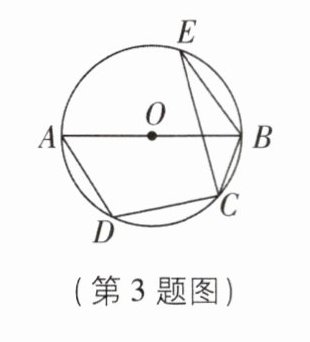
3连半径,构造圆心角[2025江苏淮安期中,中]如图,四边形ABCD是$\odot O$的内接四边形,AB是$\odot O$的直径,E为$\odot O$上一点,若$∠ADC= 110^{\circ }$,则$∠BEC$的度数为______.

答案：
20°【解析】如图，连接 OC。
∵ 四边形 ABCD 是$\odot O$的内接四边形，$∠ADC = 110^{\circ}$，$\therefore ∠CBO = 180^{\circ}-∠ADC = 180^{\circ}-110^{\circ}= 70^{\circ}$。$\because OB = OC$，$\therefore ∠BCO = ∠CBO = 70^{\circ}$，$\therefore ∠BOC = 180^{\circ}-∠BCO - ∠CBO = 40^{\circ}$，$\therefore ∠BEC = \frac{1}{2}∠BOC = 20^{\circ}$，故答案为$20^{\circ}$。

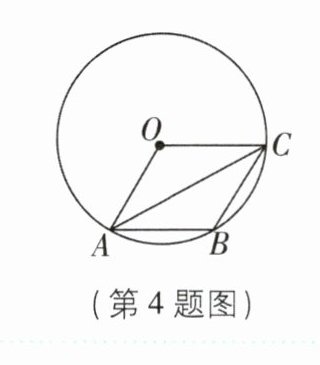
4构造圆内接四边形[2025黑龙江大庆期末,中]如图,点A,B,C在$\odot O$上,四边形OABC是平行四边形,若对角线$AC= 2\sqrt {3}$,则OA的长为______.

答案：
2 【解析】如图，在优弧 AC 上找一点 M，连接 AM，CM，OB，OB 交 AC 于点 N，则$∠AOC = 2∠AMC$。
∵ 四边形 OABC 是平行四边形，$\therefore ∠ABC = ∠AOC = 2∠AMC$。
∵ 四边形 MABC 是$\odot O$的内接四边形，$\therefore ∠AMC + ∠ABC = 180^{\circ}$，$\therefore ∠AMC + 2∠AMC = 180^{\circ}$，$\therefore ∠AMC = 60^{\circ}$，$\therefore ∠AOC = 120^{\circ}$。
∵ 四边形 OABC 是平行四边形，$AC = 2\sqrt{3}$，$\therefore AN = CN = \frac{1}{2}AC = \frac{1}{2}×2\sqrt{3}=\sqrt{3}$。$\because OA = OC$，
∴ 四边形 OABC 为菱形，$∠OAC = ∠OCA = 30^{\circ}$，$\therefore ∠AOB = ∠COB = 60^{\circ}$，$\therefore ∠ONA = 180^{\circ}-∠AOB - ∠OAC = 90^{\circ}$，$\therefore OA = 2ON$，$\therefore (2ON)^{2}=ON^{2}+(\sqrt{3})^{2}$，$\therefore ON = 1$，$\therefore OA = 2ON = 2$，故答案为 2。

5构造直角三角形[2025江苏南京质检,中]如图,$\odot O$的半径为4,$\triangle ABC$的顶点A,B在$\odot O$上,$∠B= 90^{\circ },∠A= 60^{\circ },AC,BC分别与\odot O$交于D,E两点,且$BE= DE$,则$\triangle ABC$的面积为______.

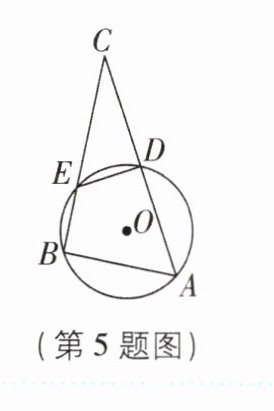
答案：
24√3 【解析】连接 AE，如图。
∵$∠CBA = 90^{\circ}$，点 A，B，E 都在$\odot O$上，
∴ AE 为$\odot O$的直径，$\therefore AE = 8$。$\because BE = DE$，$\therefore \widehat{BE}=\widehat{DE}$，$\therefore ∠BAE = ∠DAE$。$\because ∠BAC = 60^{\circ}$，$\therefore ∠BAE = ∠DAE = 30^{\circ}$，$\therefore BE = DE = \frac{1}{2}AE = 4$，$\therefore AB = \sqrt{AE^{2}-BE^{2}}=\sqrt{8^{2}-4^{2}}= 4\sqrt{3}$。
∵ AE 为直径，$\therefore ∠EDA = ∠EDC = 90^{\circ}$。$\because ∠C = 180^{\circ}-∠ABC - ∠BAC = 180^{\circ}-90^{\circ}-60^{\circ}= 30^{\circ}$，$\therefore EC = 2ED = 8$，$\therefore BC = BE + CE = 12$，$\therefore S_{△ABC}=\frac{1}{2}AB\cdot BC=\frac{1}{2}×4\sqrt{3}×12 = 24\sqrt{3}$。故答案为$24\sqrt{3}$。

6[较难]如图,$\triangle ABC$中,$AD⊥BC,∠B= 45^{\circ },∠C= 30^{\circ }$.以AD为弦的圆分别交AB,AC于E,F两点,连接ED,FD,点G在AC边上,且满足$∠EDG= 120^{\circ }$,连接EG.若$CD= 4+2\sqrt {2}$,则$\triangle DEG$的面积的最小值是______.

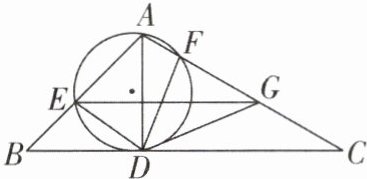
答案：
2√2+2 【解析】如图，连接 EF。
∵$AD⊥BC$，$∠B = 45^{\circ}$，$∠C = 30^{\circ}$，$\therefore ∠BAD = 45^{\circ}$，$∠DAC = 60^{\circ}$，$∠BAC = 105^{\circ}$。
∵ A，E，F，D 四点共圆，$\therefore ∠EDF = 75^{\circ}$。$\because ∠EDG = 120^{\circ}$，$\therefore ∠FDG = 45^{\circ}$。$\because \widehat{ED}=\widehat{ED}$，$\therefore ∠EFD = ∠EAD = 45^{\circ}$，$\therefore ∠EFD = ∠FDG$，$\therefore EF// DG$，$\therefore S_{△FDG}=S_{△EDG}$。$\because CD = 4 + 2\sqrt{2}$，$∠C = 30^{\circ}$，$\therefore AC = 2AD$，
∴ 易得$AD = \frac{4\sqrt{3}}{3}+\frac{2\sqrt{6}}{3}$，$AC = \frac{8\sqrt{3}}{3}+\frac{4\sqrt{6}}{3}$，
∴ AC 边上的高为$\frac{AD\cdot DC}{AC}= 2+\sqrt{2}$，
∴ 当 FG 最小时，$△DFG$的面积取得最小值。作$△DFG$的外接圆$\odot O$，过点 O 作$OH⊥FG$于点 H，连接 OF，OG，OD，DH。
∵$∠FDG = 45^{\circ}$，$\therefore ∠FOG = 90^{\circ}$。$\because OF = GO$，
∴$△FOG$是等腰直角三角形，$\therefore ∠FOH = \frac{1}{2}∠FOG = 45^{\circ}$，
∴$△FOH$是等腰直角三角形，$\therefore FH = OH = \frac{1}{2}FG$，$FO = \sqrt{2}FH$，$\therefore DO + OH = \frac{\sqrt{2}}{2}FG+\frac{1}{2}FG=\frac{1+\sqrt{2}}{2}FG$，
∴ 当 DO + OH 最小时，FG 就取得最小值。$\because DO + OH\geq DH$，
∴ 当 D，O，H 三点共线时，DO + OH 最小，此时$DH⊥FG$，$\therefore DH = 2+\sqrt{2}$。$\because DH = 2+\sqrt{2}=FH + FO = FH+\sqrt{2}FH$，$\therefore FH = \sqrt{2}$，
∴ FG 的最小值为$2\sqrt{2}$，此时$S_{△DFG}=\frac{1}{2}×2\sqrt{2}×(2+\sqrt{2})= 2\sqrt{2}+2$，$\therefore △DEG$的面积的最小值为$2\sqrt{2}+2$。故答案为$2\sqrt{2}+2$。

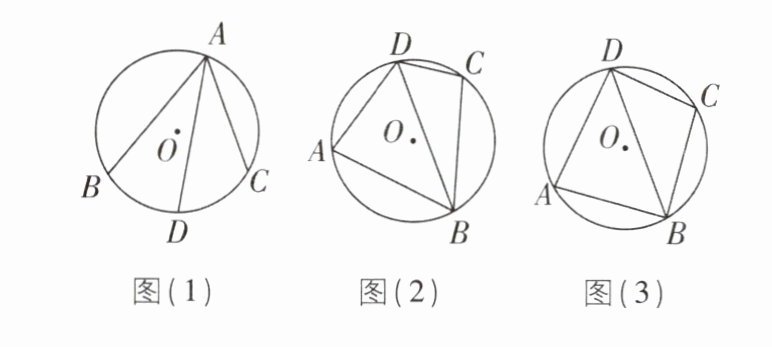
7核心素养推理能力[2024江苏徐州调研,较难]如图(1),在$\odot O$中,弦AD平分圆周角$∠BAC$,我们将圆中以A为公共点的三条弦BA,CA,DA构成的图形称为“爪形A”,弦BA,CA,DA称为“爪形A”的爪.如图(2),四边形ABCD内接于$\odot O,AB= BC$,连接BD.
(1)证明圆中存在“爪形D”.
(2)若$∠ADC= 120^{\circ }$,求证:$AD+CD= BD$.
(3)如图(3),若$AD⊥DC$,此时“爪形D”的爪之间满足怎样的数量关系,请直接写出结果.

答案：

(1)【证明】$\because AB = BC$，$\therefore ∠ADB = ∠CDB$，
∴ DB 平分圆周角$∠ADC$，
∴ 圆中存在“爪形 D”。
(2)【证明】如图
(1)，延长 DC 至点 E，使得$CE = AD$，连接 BE。$\because ∠A + ∠DCB = 180^{\circ}$，$∠ECB + ∠DCB = 180^{\circ}$，$\therefore ∠A = ∠ECB$。$\because CE = AD$，$AB = BC$，$\therefore △BAD\cong △BCE$，$\therefore ∠E = ∠ADB$。$\because ∠ADC = 120^{\circ}$，$\therefore ∠E = ∠ADB = ∠BDC = 60^{\circ}$，$\therefore △BDE$为等边三角形，$\therefore DE = BD$，$\therefore AD + CD = BD$。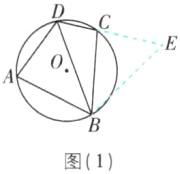
(3)【解】$AD + CD = \sqrt{2}BD$。如图
(2)，延长 DC 至点 E，使得$CE = AD$，连接 BE。同
(2)可得$△BAD\cong △BCE$，$\therefore ∠E = ∠ADB$，$BD = BE$。$\because AD⊥DC$，$\therefore ∠E = ∠ADB = ∠BDE = 45^{\circ}$，$\therefore ∠DBE = 90^{\circ}$，$\therefore △BDE$为等腰直角三角形，$\therefore DE = \sqrt{2}BD$，即$AD + CD = \sqrt{2}BD$。