第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1 [2025江苏常州调研]如图,$\odot O和直线l_{1}$、直线$l_{2}$在同一平面内,AB是$\odot O$的直径,直线$l_{2}是\odot O$的切线,切点为B,直线$l_{1}$经过点A,下列条件不能判定直线$l_{1}与\odot O$相切的是(
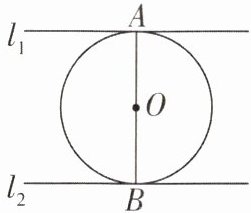
A.$l_{1}// l_{2}$
B.$l_{1}⊥AB$
C.$l_{1}与\odot O$只有一个公共点
D.点O到$l_{1}$上某点的距离等于半径
D
)
A.$l_{1}// l_{2}$
B.$l_{1}⊥AB$
C.$l_{1}与\odot O$只有一个公共点
D.点O到$l_{1}$上某点的距离等于半径
答案:
1.D 【解析】
∵ AB是⊙O的直径,且l₂是⊙O的切线,切点为B,
∴ l₂⊥AB. 又
∵ l₁//l₂,
∴ l₁⊥AB,
∴ 直线l₁与⊙O相切,故选项A、B可以判定,不符合题意. 根据圆的切线的定义,可知与圆仅有一个公共点的直线是切线,故选项C可以判定,不符合题意. D选项无法判定直线l₁与⊙O相切. 故选D.
∵ AB是⊙O的直径,且l₂是⊙O的切线,切点为B,
∴ l₂⊥AB. 又
∵ l₁//l₂,
∴ l₁⊥AB,
∴ 直线l₁与⊙O相切,故选项A、B可以判定,不符合题意. 根据圆的切线的定义,可知与圆仅有一个公共点的直线是切线,故选项C可以判定,不符合题意. D选项无法判定直线l₁与⊙O相切. 故选D.
2 如图,点B在$\odot A$上,点C在$\odot A$外,以下条件不能判定BC是$\odot A$切线的是(
A.$∠A= 50^{\circ },∠C= 40^{\circ }$
B.$∠B-∠C= ∠A$
C.$AB^{2}+BC^{2}= AC^{2}$
D.$\odot A$与AC的交点是AC中点
D
)A.$∠A= 50^{\circ },∠C= 40^{\circ }$
B.$∠B-∠C= ∠A$
C.$AB^{2}+BC^{2}= AC^{2}$
D.$\odot A$与AC的交点是AC中点
答案:
2.D 【解析】A选项,
∵ ∠A = 50°,∠C = 40°,
∴ ∠B = 180° - ∠A - ∠C = 90°,
∴ BC⊥AB.
∵ 点B在⊙A上,
∴ AB是⊙A的半径,
∴ BC是⊙A的切线. B选项,
∵ ∠B - ∠C = ∠A,
∴ ∠B = ∠A + ∠C.
∵ ∠A + ∠B + ∠C = 180°,
∴ ∠B = 90°,
∴ BC⊥AB.
∵ 点B在⊙A上,
∴ AB是⊙A的半径,
∴ BC是⊙A的切线.
易错警示:片面地在半径外端找点,而忽视直线另一侧圆上符合条件的点,就会出错.
思路分析:连接OC,由CE为⊙O的切线可得OC⊥CE,由OA = OC得到∠OAC = ∠OCA = 25°,再利用外角性质求出∠COE的度数,即可求出∠E的度数.
C选项,
∵ AB² + BC² = AC²,
∴ △ABC是直角三角形,且∠B = 90°,
∴ BC⊥AB.
∵ 点B在⊙A上,
∴ AB是⊙A的半径,
∴ BC是⊙A的切线.
D选项,
∵ ⊙A与AC的交点是AC中点,
∴ AB = $\frac{1}{2}$AC,但不能证出∠B = 90°,
∴ 不能判定BC是⊙A的切线. 故选D.
∵ ∠A = 50°,∠C = 40°,
∴ ∠B = 180° - ∠A - ∠C = 90°,
∴ BC⊥AB.
∵ 点B在⊙A上,
∴ AB是⊙A的半径,
∴ BC是⊙A的切线. B选项,
∵ ∠B - ∠C = ∠A,
∴ ∠B = ∠A + ∠C.
∵ ∠A + ∠B + ∠C = 180°,
∴ ∠B = 90°,
∴ BC⊥AB.
∵ 点B在⊙A上,
∴ AB是⊙A的半径,
∴ BC是⊙A的切线.
易错警示:片面地在半径外端找点,而忽视直线另一侧圆上符合条件的点,就会出错.
思路分析:连接OC,由CE为⊙O的切线可得OC⊥CE,由OA = OC得到∠OAC = ∠OCA = 25°,再利用外角性质求出∠COE的度数,即可求出∠E的度数.
C选项,
∵ AB² + BC² = AC²,
∴ △ABC是直角三角形,且∠B = 90°,
∴ BC⊥AB.
∵ 点B在⊙A上,
∴ AB是⊙A的半径,
∴ BC是⊙A的切线.
D选项,
∵ ⊙A与AC的交点是AC中点,
∴ AB = $\frac{1}{2}$AC,但不能证出∠B = 90°,
∴ 不能判定BC是⊙A的切线. 故选D.
3 新考向开放性试题如图,AB是$\odot O$的直径,要使得直线AT是$\odot O$的切线,需要添加的一个条件是
∠TAC = ∠B
.(写一个条件即可)
答案:
3.∠TAC = ∠B(答案不唯一) 【解析】
∵ AB是⊙O的直径,
∴ ∠ACB = 90°,
∴ ∠B + ∠BAC = 90°.
∵ ∠TAC = ∠B,
∴ ∠TAC + ∠BAC = 90°,即∠OAT = 90°.
∵ OA是⊙O的半径,
∴ 直线AT是⊙O的切线. 故答案为∠TAC = ∠B(答案不唯一).
∵ AB是⊙O的直径,
∴ ∠ACB = 90°,
∴ ∠B + ∠BAC = 90°.
∵ ∠TAC = ∠B,
∴ ∠TAC + ∠BAC = 90°,即∠OAT = 90°.
∵ OA是⊙O的半径,
∴ 直线AT是⊙O的切线. 故答案为∠TAC = ∠B(答案不唯一).
4 [2024辽宁大连质检]如图,已知$\odot O是\triangle ABC$的外接圆,AB是$\odot O$的直径,D是AB延长线上的一点,$AE⊥CD$交DC的延长线于E,$CF⊥AB$于F,且$CE= CF$.
(1)求证:DE是$\odot O$的切线;
(2)若$AB= 10,BD= 3$,求AE的长.
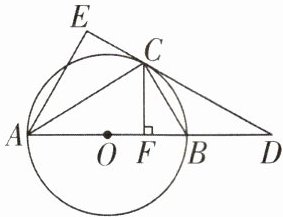
(1)求证:DE是$\odot O$的切线;
(2)若$AB= 10,BD= 3$,求AE的长.

答案:
4.
(1)【证明】连接OC,如图.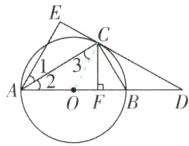
∵ AE⊥CD,CF⊥AB,且CE = CF,
∴ ∠1 = ∠2.
∵ OA = OC,
∴ ∠2 = ∠3,
∴ ∠1 = ∠3,
∴ OC//AE,
∴ OC⊥CD.
∵ OC是⊙O的半径,
∴ DE是⊙O的切线.
(2)【解】
∵ OC⊥ED,AB = 10,BD = 3,
∴ OB = OC = 5,
∴ OD = 8,
∴ CD = $\sqrt{OD² - OC²}$ = $\sqrt{39}$.
∵ S△OCD = $\frac{1}{2}$OC·CD = $\frac{1}{2}$OD·CF,
∴ $\frac{1}{2}$×5×$\sqrt{39}$ = $\frac{1}{2}$×8×CF,
∴ CF = $\frac{5\sqrt{39}}{8}$,
∴ OF = $\sqrt{OC² - FC²}$ = $\frac{25}{8}$,
∴ AF = OA + OF = 5 + $\frac{25}{8}$ = $\frac{65}{8}$. 在Rt△AEC和Rt△AFC中,CE = CF,AC = AC,
∴ Rt△AEC≌Rt△AFC(HL),
∴ AE = AF = $\frac{65}{8}$.
4.
(1)【证明】连接OC,如图.

∵ AE⊥CD,CF⊥AB,且CE = CF,
∴ ∠1 = ∠2.
∵ OA = OC,
∴ ∠2 = ∠3,
∴ ∠1 = ∠3,
∴ OC//AE,
∴ OC⊥CD.
∵ OC是⊙O的半径,
∴ DE是⊙O的切线.
(2)【解】
∵ OC⊥ED,AB = 10,BD = 3,
∴ OB = OC = 5,
∴ OD = 8,
∴ CD = $\sqrt{OD² - OC²}$ = $\sqrt{39}$.
∵ S△OCD = $\frac{1}{2}$OC·CD = $\frac{1}{2}$OD·CF,
∴ $\frac{1}{2}$×5×$\sqrt{39}$ = $\frac{1}{2}$×8×CF,
∴ CF = $\frac{5\sqrt{39}}{8}$,
∴ OF = $\sqrt{OC² - FC²}$ = $\frac{25}{8}$,
∴ AF = OA + OF = 5 + $\frac{25}{8}$ = $\frac{65}{8}$. 在Rt△AEC和Rt△AFC中,CE = CF,AC = AC,
∴ Rt△AEC≌Rt△AFC(HL),
∴ AE = AF = $\frac{65}{8}$.
5 [2024江苏扬州邗江区期末]如图,AB是$\odot O$的直径,C,D是$\odot O$上的点,$∠CDB= 25^{\circ }$,过点C作$\odot O$的切线交AB的延长线于点E,则$∠E$等于( )
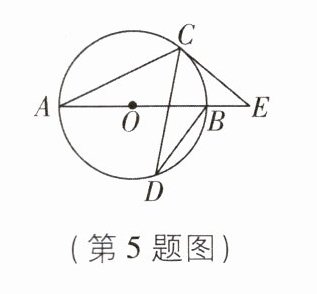
A.$40^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$30^{\circ }$

A.$40^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$30^{\circ }$
答案:
5.A 【解析】连接OC,如图.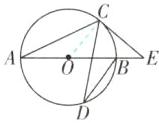
∵ CE为⊙O的切线,
∴ OC⊥CE,
∴ ∠OCE = 90°.
∵ ∠CDB = 25°,
∴ ∠BAC = ∠CDB = 25°.
∵ OA = OC,
∴ ∠OAC = ∠OCA = 25°,
∴ ∠COE = 50°,
∴ ∠E = 40°. 故选A.
5.A 【解析】连接OC,如图.
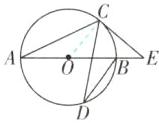
∵ CE为⊙O的切线,
∴ OC⊥CE,
∴ ∠OCE = 90°.
∵ ∠CDB = 25°,
∴ ∠BAC = ∠CDB = 25°.
∵ OA = OC,
∴ ∠OAC = ∠OCA = 25°,
∴ ∠COE = 50°,
∴ ∠E = 40°. 故选A.
6 已知AB为$\odot O$的直径,$AB= 6$,C为$\odot O$上一点,连接CA,CB.如图,若$AC= 2$,OD为$\odot O$的半径,且$OD⊥CB$,垂足为E,过点D作$\odot O$的切线,与AC的延长线相交于点F,则FD的长为____
2$\sqrt{2}$
.
答案:
6.2$\sqrt{2}$
思路分析:利用切线的性质求线段长:∠FCB = ∠CED = 90°→四边形CEDF为矩形→求得FD的长;∠ODF = 90°,勾股定理→BC的长→CE的长
【解析】
∵ AB为⊙O的直径,
∴ ∠ACB = 90°,
∴ ∠FCB = 90°.
∵ DF是⊙O的切线,
∴ OD⊥DF,
∴ ∠ODF = 90°.
∵ OD⊥BC,
∴ ∠CED = 90°,
∴ 四边形FCED为矩形,
∴ FD = EC. 在Rt△ABC中,∠ACB = 90°,AC = 2,AB = 6,
∴ BC = $\sqrt{AB² - AC²}$ = 4$\sqrt{2}$;
∵ OD⊥BC,
∴ EC = $\frac{1}{2}$BC = 2$\sqrt{2}$,
∴ FD = 2$\sqrt{2}$. 故答案为2$\sqrt{2}$.
思路分析:利用切线的性质求线段长:∠FCB = ∠CED = 90°→四边形CEDF为矩形→求得FD的长;∠ODF = 90°,勾股定理→BC的长→CE的长
【解析】
∵ AB为⊙O的直径,
∴ ∠ACB = 90°,
∴ ∠FCB = 90°.
∵ DF是⊙O的切线,
∴ OD⊥DF,
∴ ∠ODF = 90°.
∵ OD⊥BC,
∴ ∠CED = 90°,
∴ 四边形FCED为矩形,
∴ FD = EC. 在Rt△ABC中,∠ACB = 90°,AC = 2,AB = 6,
∴ BC = $\sqrt{AB² - AC²}$ = 4$\sqrt{2}$;
∵ OD⊥BC,
∴ EC = $\frac{1}{2}$BC = 2$\sqrt{2}$,
∴ FD = 2$\sqrt{2}$. 故答案为2$\sqrt{2}$.
7 [2025江苏南通调研]如图,四边形ABCD是$\odot O$的内接四边形,$∠A= 90^{\circ }$,D为$\overset{\frown }{AC}$的中点,AD,BC的延长线交于点E,$\odot O$的切线DF与BE交于点F.
(1)求证:DF是$∠CDE$的平分线;
(2)若$∠E= 30^{\circ },BE= 6$,求CF的长.
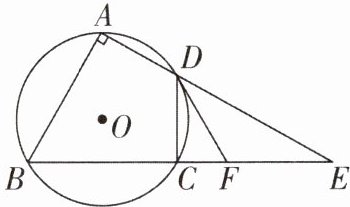
(1)求证:DF是$∠CDE$的平分线;
(2)若$∠E= 30^{\circ },BE= 6$,求CF的长.

答案:
7.
(1)【证明】如图,连接BD.
∵ ∠A = 90°,
∴ BD是⊙O的直径.
∵ DF是⊙O的切线,
∴ ∠BCD = ∠BDF = 90°.
∵ D是$\overset{\frown}{AC}$的中点,
∴ ∠ABD = ∠CBD,
∴ ∠BDA = ∠BDC.
∵ ∠BDF = 90°,
∴ ∠BDA + ∠FDE = 90°,∠BDC + ∠CDF = 90°,
∴ ∠FDE = ∠CDF,
∴ DF是∠CDE的平分线.
(2)【解】
∵ ∠E = 30°,
∴ ∠ABE = 60°,
∴ ∠ABD = ∠EBD = 30°,即∠EBD = ∠E,
∴ DB = DE.
∵ ∠BCD = 90°,
∴ BC = CE = $\frac{1}{2}$BE = 3. 在Rt△BCD中,BD = 2CD,BD² = CD² + BC²,
∴ 4CD² = CD² + 3²,
∴ CD = $\sqrt{3}$. 在Rt△CDF中,∠CDF = $\frac{1}{2}$∠CDE = $\frac{1}{2}$(90° - ∠E) = 30°,
∴ DF = 2CF.
∵ DF² = CD² + CF²,
∴ 4CF² = ($\sqrt{3}$)² + CF²,
∴ CF = 1.
7.
(1)【证明】如图,连接BD.
∵ ∠A = 90°,
∴ BD是⊙O的直径.
∵ DF是⊙O的切线,
∴ ∠BCD = ∠BDF = 90°.
∵ D是$\overset{\frown}{AC}$的中点,
∴ ∠ABD = ∠CBD,
∴ ∠BDA = ∠BDC.
∵ ∠BDF = 90°,
∴ ∠BDA + ∠FDE = 90°,∠BDC + ∠CDF = 90°,
∴ ∠FDE = ∠CDF,
∴ DF是∠CDE的平分线.

(2)【解】
∵ ∠E = 30°,
∴ ∠ABE = 60°,
∴ ∠ABD = ∠EBD = 30°,即∠EBD = ∠E,
∴ DB = DE.
∵ ∠BCD = 90°,
∴ BC = CE = $\frac{1}{2}$BE = 3. 在Rt△BCD中,BD = 2CD,BD² = CD² + BC²,
∴ 4CD² = CD² + 3²,
∴ CD = $\sqrt{3}$. 在Rt△CDF中,∠CDF = $\frac{1}{2}$∠CDE = $\frac{1}{2}$(90° - ∠E) = 30°,
∴ DF = 2CF.
∵ DF² = CD² + CF²,
∴ 4CF² = ($\sqrt{3}$)² + CF²,
∴ CF = 1.
8 [2023山东滨州中考]如图,PA,PB分别与$\odot O$相切于A,B两点,且$∠APB= 56^{\circ }$.若点C是$\odot O$上异于点A,B的一点,则$∠ACB$的大小为____.
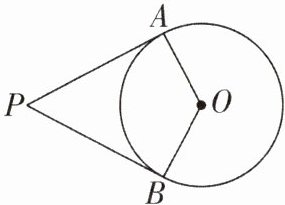

答案:
8.62°或118° 【解析】如图所示,连接AC,BC. 当点C在优弧ACB上时,
∵ PA,PB分别与⊙O相切于A,B两点,
∴ ∠PAO = ∠PBO = 90°.
∵ ∠APB = 56°,
∴ ∠AOB = 360° - 90° - 90° - 56° = 124°,
∴ ∠ACB = $\frac{1}{2}$∠AOB = 62°. 当点C'在劣弧AB上时,
∵ 四边形AC'BC是⊙O的内接四边形,
∴ ∠C' = 180° - ∠C = 118°. 故答案为62°或118°.

易错警示:根据切线的性质得到∠PAO = ∠PBO = 90°,根据四边形内角和为360°,得出∠AOB的度数. 点C是⊙O上异于点A,B的一点,故点C可能在劣弧AB或在优弧ACB上,需分两种情况求解,不能漏解.
8.62°或118° 【解析】如图所示,连接AC,BC. 当点C在优弧ACB上时,
∵ PA,PB分别与⊙O相切于A,B两点,
∴ ∠PAO = ∠PBO = 90°.
∵ ∠APB = 56°,
∴ ∠AOB = 360° - 90° - 90° - 56° = 124°,
∴ ∠ACB = $\frac{1}{2}$∠AOB = 62°. 当点C'在劣弧AB上时,
∵ 四边形AC'BC是⊙O的内接四边形,
∴ ∠C' = 180° - ∠C = 118°. 故答案为62°或118°.

易错警示:根据切线的性质得到∠PAO = ∠PBO = 90°,根据四边形内角和为360°,得出∠AOB的度数. 点C是⊙O上异于点A,B的一点,故点C可能在劣弧AB或在优弧ACB上,需分两种情况求解,不能漏解.
查看更多完整答案,请扫码查看


