第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1[2024江苏徐州期中]下列四边形的四个顶点,一定在同一个圆上的是(
A.平行四边形
B.矩形
C.菱形
D.梯形
B
)A.平行四边形
B.矩形
C.菱形
D.梯形
答案:
B [解析]四个顶点在同一个圆上的四边形,一定满足有一点到它的四个顶点的距离都相等,因而A、C、D都是错误的.
∵矩形对角线相等且互相平分,
∴四个顶点到对角线交点的距离相等,
∴矩形的四个顶点一定在同一个圆上.故选B.
∵矩形对角线相等且互相平分,
∴四个顶点到对角线交点的距离相等,
∴矩形的四个顶点一定在同一个圆上.故选B.
2如图,点A,D,G,M在半圆O上,四边形ABOC,DEOF,HMNO均为矩形.设BC= a,EF= b,NH= c,则a,b,c三者间的大小关系为( )
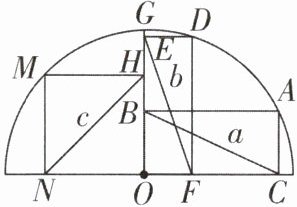
A.a>b>c
B.a= b= c
C.c>a>b
D.b>c>a

A.a>b>c
B.a= b= c
C.c>a>b
D.b>c>a
答案:
B
思路分析
连接→OM,OD,OA
↓
比较→OM=OD=OA
↓
转化→HN=EF=BC
[解析]连接OM,OD,OA,如图.
∵点A,D,M在半圆上,
∴ OM=OD=OA.
∵四边形ABOC,DEOF,HMNO均为矩形,
∴ OM=NH,OD=EF,OA=BC,
∴ BC=EF=HN,即a=b=c.故选B.

B
思路分析
连接→OM,OD,OA
↓
比较→OM=OD=OA
↓
转化→HN=EF=BC
[解析]连接OM,OD,OA,如图.
∵点A,D,M在半圆上,
∴ OM=OD=OA.
∵四边形ABOC,DEOF,HMNO均为矩形,
∴ OM=NH,OD=EF,OA=BC,
∴ BC=EF=HN,即a=b=c.故选B.

3[2025浙江绍兴期末]如图,以点A为圆心的圆交数轴于B,C两点(点C在点A的左侧,点B在点A的右侧),若A,B两点表示的数分别为1,$\sqrt{3}$,则点C表示的数是
$2-\sqrt{3}$
.
答案:
$2-\sqrt{3}$ [解析]
∵A,B两点表示的数分别为$1,\sqrt{3}$,
∴$AC=AB=\sqrt{3}-1$,
∴点C表示的数是$1-(\sqrt{3}-1)=2-\sqrt{3}$.故答案为$2-\sqrt{3}$.
∵A,B两点表示的数分别为$1,\sqrt{3}$,
∴$AC=AB=\sqrt{3}-1$,
∴点C表示的数是$1-(\sqrt{3}-1)=2-\sqrt{3}$.故答案为$2-\sqrt{3}$.
4[2024江苏南京期中]已知⊙O的半径为5,点P在⊙O内,则OP的长可能是(
A.7
B.6
C.5
D.4
D
)A.7
B.6
C.5
D.4
答案:
D [解析]
∵⊙O的半径为5,点P在⊙O内,
∴OP<5.故选D.
∵⊙O的半径为5,点P在⊙O内,
∴OP<5.故选D.
5[2025浙江宁波质检]如图,已知⊙O的半径为3,平面内有一点到圆心O的距离为4,则该点可能是(
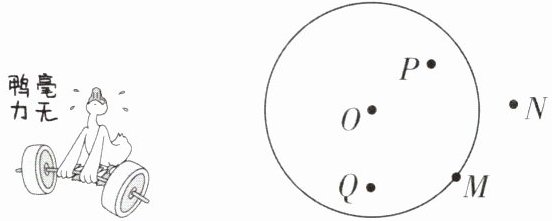
A.点P
B.点Q
C.点M
D.点N
D
)
A.点P
B.点Q
C.点M
D.点N
答案:
D [解析]
∵平面内有一点到圆心O的距离为4,⊙O的半径为3,4>3,
∴该点在⊙O外,
∴只有点N符合要求,故选D.
∵平面内有一点到圆心O的距离为4,⊙O的半径为3,4>3,
∴该点在⊙O外,
∴只有点N符合要求,故选D.
6[2025江苏无锡调研]如图,数轴上半径为1的⊙O从原点O开始以每秒2个单位的速度向右运动,在原点右侧且距原点7个单位处有一点P,经过
3或4
秒,点P在⊙O上.
答案:
3或4 [解析]当点P第一次在⊙O上时,(7−1)÷2=3(秒);当点P第二次在⊙O上时,[7−(−1)]÷2=4(秒).综上所述,经过3秒或4秒,点P在⊙O上.故答案为3或4.
在Rt△ABC中,∠C= 90°,AC= 4cm,BC= 3cm,D是AB边的中点,以点C为圆心,2.4cm为半径作圆,则点D与⊙C的位置关系是
点D在⊙C外
.
答案:
点D在⊙C外 [解析]在Rt△ABC中,AC = 4cm,BC = 3cm,
∴$AB=\sqrt{AC^2+BC^2}=\sqrt{4^2+3^2}=5$(cm).
∵D是AB边的中点,
∴$CD=\frac{1}{2}AB = 2.5$(cm),即点D到圆心C的距离为2.5cm.
∵⊙C的半径为2.4cm,2.5>2.4,
∴点D在⊙C外.故答案为点D在⊙C外.
∴$AB=\sqrt{AC^2+BC^2}=\sqrt{4^2+3^2}=5$(cm).
∵D是AB边的中点,
∴$CD=\frac{1}{2}AB = 2.5$(cm),即点D到圆心C的距离为2.5cm.
∵⊙C的半径为2.4cm,2.5>2.4,
∴点D在⊙C外.故答案为点D在⊙C外.
8如图所示,D为等边△ABC的边BC的中点,AB= 2,动点M满足AM⊥CM.
(1)求证:点A,D,C,M在同一个圆上;
(2)连接BM,求线段BM的最大值与最小值.
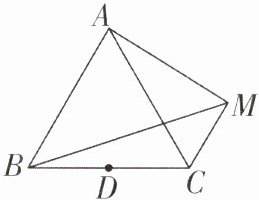
(1)求证:点A,D,C,M在同一个圆上;
(2)连接BM,求线段BM的最大值与最小值.

答案:
(1)[证明]如图,连接AD,取AC的中点O,连接OD,OM.
∵△ABC是等边三角形,BD = DC,
∴AD⊥BC.
∵AM⊥CM,
∴∠ADC = ∠AMC = 90°.
∵OA = OC,
∴OD = OA = OC = OM,
∴点A,D,C,M在同一个圆上.
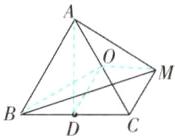
(2)[解]如图,连接OB.
∵AB = AC = BC = 2,AO = OC,
∴BO⊥AC,
∴$BO=\sqrt{AB^2 - AO^2}=\sqrt{2^2 - 1^2}=\sqrt{3}$.
∵$OB - OM\leq BM\leq OB + OM$,且OM = OA = OC = 1,
∴$\sqrt{3}-1\leq BM\leq \sqrt{3}+1$,
∴BM的最大值为$\sqrt{3}+1$,最小值为$\sqrt{3}-1$.
(1)[证明]如图,连接AD,取AC的中点O,连接OD,OM.
∵△ABC是等边三角形,BD = DC,
∴AD⊥BC.
∵AM⊥CM,
∴∠ADC = ∠AMC = 90°.
∵OA = OC,
∴OD = OA = OC = OM,
∴点A,D,C,M在同一个圆上.

(2)[解]如图,连接OB.
∵AB = AC = BC = 2,AO = OC,
∴BO⊥AC,
∴$BO=\sqrt{AB^2 - AO^2}=\sqrt{2^2 - 1^2}=\sqrt{3}$.
∵$OB - OM\leq BM\leq OB + OM$,且OM = OA = OC = 1,
∴$\sqrt{3}-1\leq BM\leq \sqrt{3}+1$,
∴BM的最大值为$\sqrt{3}+1$,最小值为$\sqrt{3}-1$.
9点P是非圆上一点,若点P到⊙O上的点的最小距离是4cm,最大距离是9cm,则⊙O的半径是____.
答案:
6.5cm或2.5cm [解析]分为两种情况:①当点P在圆内时,如图
(1),
∵点P到圆上的最小距离PB = 4cm,最大距离PA = 9cm,
∴直径AB = 4 + 9 = 13(cm),
∴半径是6.5cm;②当点P在圆外时,如图
(2),
∵点P到圆上的最小距离PB = 4cm,最大距离PA = 9cm,
∴直径AB = 9 - 4 = 5(cm),
∴半径是2.5cm.故答案为6.5cm或2.5cm.


6.5cm或2.5cm [解析]分为两种情况:①当点P在圆内时,如图
(1),
∵点P到圆上的最小距离PB = 4cm,最大距离PA = 9cm,
∴直径AB = 4 + 9 = 13(cm),
∴半径是6.5cm;②当点P在圆外时,如图
(2),
∵点P到圆上的最小距离PB = 4cm,最大距离PA = 9cm,
∴直径AB = 9 - 4 = 5(cm),
∴半径是2.5cm.故答案为6.5cm或2.5cm.


查看更多完整答案,请扫码查看


