《2025年初中必刷题九年级数学上册苏科版》

1 [中]元旦来临前,某商场将一件原价为 a 元的衬衫以一个给定的百分比提升价格,元旦那天商场又按照新的价格以相同的百分比降低了这件衬衫的价格,最终,衬衫的价格比原价降低了 0.16a 元,则这个给定的百分比为 (C)
A.16%
B.36%
C.40%
D.50%

答案： C 【解析】设这个给定的百分比为 x. 根据题意,得$a(1 + x)(1 - x)=a - 0.16a$,解得$x_{1}=0.4 = 40\% $,$x_{2}=-0.4$(舍去),即这个给定的百分比为 40%. 故选 C.

两年前生产 1 吨甲种药品的成本是 5000 元,生产 1 吨乙种药品的成本是 6000 元,随着生产技术的进步,现在生产 1 吨甲种药品的成本是 3000 元,生产 1 吨乙种药品的成本是 3600 元,如果甲药品成本的年平均下降率为 x,乙药品成本的年平均下降率 y,则 x 与 y 的大小关系为 (A)
A.x = y
B.x ＞ y
C.x ＜ y
D.无法比较

答案： A 【解析】由题意得$5000(1 - x)^{2}=3000$,$6000(1 - y)^{2}=3600$,整理得$(1 - x)^{2}=\frac{3}{5}$,$(1 - y)^{2}=\frac{3}{5}$,$\therefore (1 - x)^{2}=(1 - y)^{2}$,$\therefore 1 - x = 1 - y$或$1 - x = -(1 - y)$,$\therefore x = y$或$x + y = 2$(不合题意,舍去),$\therefore x = y$. 故选 A.

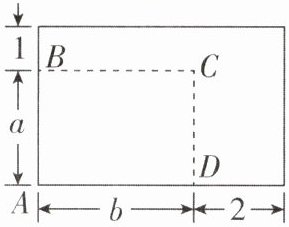
3 [2025 江苏宿迂期中,中]如图是一块长方形菜地 ABCD,AB = a m,AD = b m,面积为$ S m^2。$现将边 AB 增加 1 m,边 AD 增加 2 m,若有且只有一个 a 的值,使得到的长方形面积为$ 2S m^2,$则 S 的值是 $6 + 4\sqrt{2}$。

答案： $6 + 4\sqrt{2}$【解析】根据题意得,$S = ab$,$2S = (a + 1)(b + 2)$,$\therefore b = \frac{S}{a}$,$\therefore 2S = (a + 1)(\frac{S}{a}+2)$.关键点拨:
(2)解本题的关键是列出一元二次方程,再利用根的判别式判断方程有无实数根.关键点拨:解本题的关键是得到以 S 为参数的关于 a 的一元二次方程,再由方程有两个相等的实数根求出参数 S 的值.$\therefore 2a^{2}+(2 - S)a + S = 0$.
∵ 有且只有一个 a 的值使之成立,$\therefore (2 - S)^{2}-8S = 0$,整理得$S^{2}-12S + 4 = 0$,解得$S_{1}=6 + 4\sqrt{2}$,$S_{2}=6 - 4\sqrt{2}$(舍去),
∴ S 的值是$6 + 4\sqrt{2}$. 故答案为$6 + 4\sqrt{2}$.

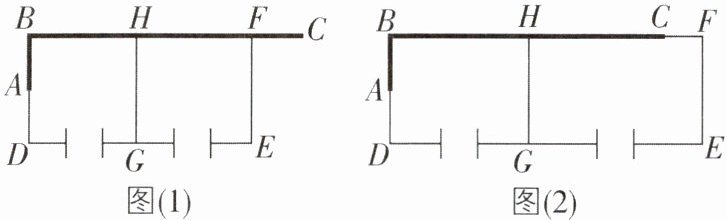
4 [2024 浙江湖州长兴期中,中]某牧场准备利用现成的一堵“7”字形的墙面(粗线 A - B - C 表示墙面)建饲养场,已知 AB ⊥ BC,AB = 3 米,BC = 15 米,现计划用总长为 38 米的篱笆围建一个“日”字形的饲养场 BDEF,并在每个区域开一个宽 2 米的门,如图(细线表示篱笆,饲养场中间用篱笆 GH 隔开),点 F 可能在线段 BC 上,也可能在线段 BC 的延长线上。
(1)如图(1),当点 F 在线段 BC 上时,若围成的饲养场 BDEF 的面积为 132 平方米,求饲养场的宽 EF 的长；
(2)如图(2),当点 F 在线段 BC 延长线上时,所围成的饲养场 BDEF 的面积能否为 156 平方米？如果能,求出 EF 的长；如果不能,请说明理由。

答案： 【解】
(1)设 EF 的长为 x 米,则$DE = 38 + 2 + 2-(3x - 3)=(45 - 3x)$米.依题意得$x(45 - 3x)=132$,整理得$x^{2}-15x + 44 = 0$,解得$x_{1}=4$,$x_{2}=11$.当$x = 4$时,$45 - 3x = 45 - 3×4 = 33 ＞ 15$,不合题意,舍去;当$x = 11$时,$45 - 3x = 45 - 3×11 = 12 ＜ 15$,符合题意.答:饲养场的宽 EF 的长为 11 米.
(2)不能. 理由如下:设 EF 的长为 y 米,则$DE=\frac{38 + 15 + 2 + 2-(3y - 3)}{2}=\frac{60 - 3y}{2}$(米).依题意,得$y\cdot\frac{60 - 3y}{2}=156$.整理,得$y^{2}-20y + 104 = 0$.$\because (-20)^{2}-4×1×104 = -16 ＜ 0$,
∴ 该方程没有实数根,即所围成的饲养场 BDEF 的面积不能为 156 平方米.

已知在长方形纸片 ABCD 中,AB = 6,AD = 5,现将两个边长分别为 a 和 b 的正方形纸片按图(1)、图(2)两种方式放置(图(1)、图(2)中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图(1)中阴影部分的面积为$ S_1,$图(2)中阴影部分的面积为$ S_2,$若$ S_2 - S_1 = 3,$则 b = 3；在边长为 a 的大正方形纸片的左上角摆放一个边长为 b 的小正方形纸片,如图(3),若$ S_1 = 8,$则图(3)中阴影部分的面积$ S_3 = $$\frac{13}{2}$。

答案： 3 $\frac{13}{2}$【解析】根据题意得$S_{1}=S_{长方形ABCD}-S_{大正方形}-S_{小正方形}+S_{大、小正方形重叠部分}$,$\therefore S_{1}=6×5 - a^{2}-b^{2}+(a + b - 6)b=-a^{2}+ab - 6b + 30$.同理,$S_{2}=S_{长方形ABCD}-S_{大正方形}-S_{小正方形}+S_{大、小正方形重叠部分}$,$\therefore S_{2}=6×5 - a^{2}-b^{2}+(a + b - 5)b=-a^{2}+ab - 5b + 30$,$\therefore S_{2}-S_{1}=(-a^{2}+ab - 5b + 30)-(-a^{2}+ab - 6b + 30)=b$.$\because S_{2}-S_{1}=3$,$\therefore b = 3$.又$\because S_{1}=8$,$\therefore -a^{2}+ab - 6b + 30 = 8$.将$b = 3$代入$-a^{2}+ab - 6b + 30 = 8$,得$-a^{2}+3a - 6×3 + 30 = 8$,即$a^{2}-3a - 4 = 0$,解得$a_{1}=4$,$a_{2}=-1$(舍去),$\therefore a = 4$.根据题意,得$S_{3}=S_{大正方形}+S_{小正方形}-S_{左上空白直角三角形}-S_{右下空白直角三角形}$,$\therefore S_{3}=a^{2}+b^{2}-\frac{1}{2}(a + b)b-\frac{1}{2}a^{2}=\frac{1}{2}a^{2}+\frac{1}{2}b^{2}-\frac{1}{2}ab=\frac{1}{2}×4^{2}+\frac{1}{2}×3^{2}-\frac{1}{2}×4×3=\frac{13}{2}$.故答案为 3,$\frac{13}{2}$.