第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1 如图,已知PA切⊙O于点A,⊙O的半径为3,OP= 5,则切线PA的长为 (

A.$\sqrt{34}$
B.8
C.4
D.2
C
)
A.$\sqrt{34}$
B.8
C.4
D.2
答案:
C 【解析】连接OA.
∵PA切⊙O于点A,
∴OA⊥AP.在Rt△OAP中,PA=√(OP² - OA²)=√(5² - 3²)=4.故选C.
∵PA切⊙O于点A,
∴OA⊥AP.在Rt△OAP中,PA=√(OP² - OA²)=√(5² - 3²)=4.故选C.
如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD= 2,BC= 5,则△ABC的周长为 (
A.7
B.14
C.10
D.4
B
)A.7
B.14
C.10
D.4
答案:
B 【解析】
∵△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,
∴AF=AD=2,BD=BE,CF=CE,
∴BD+CF=BE+CE=BC=5,
∴△ABC的周长为AD+DB+BC+CF+AF=AD+AF+BC+(BD+CF)=14,故选B.
∵△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,
∴AF=AD=2,BD=BE,CF=CE,
∴BD+CF=BE+CE=BC=5,
∴△ABC的周长为AD+DB+BC+CF+AF=AD+AF+BC+(BD+CF)=14,故选B.
3 [2024江苏南通海安期中]如图,AB是⊙O的直径,DB,DE是⊙O的两条切线,切点分别为B,C.若∠ACE= 25°,则∠D的度数为 ( )
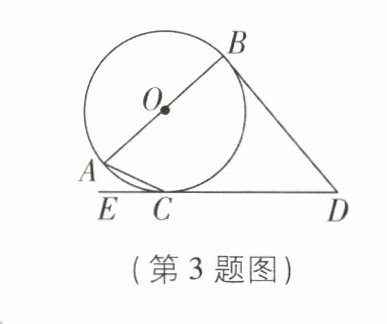
A.50°
B.55°
C.60°
D.65°

A.50°
B.55°
C.60°
D.65°
答案:
A 【解析】连接BC,如图.
∵DB,DC是⊙O的切线,切点分别是B,C,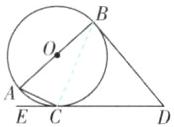
∴DB=DC,
∴∠DBC=∠DCB.
∵AB是直径,
∴∠ACB=90°.
∵∠ACE=25°,
∴∠DBC=∠DCB=65°,
∴∠D=180° - 65°×2=50°.故选A.
A 【解析】连接BC,如图.
∵DB,DC是⊙O的切线,切点分别是B,C,

∴DB=DC,
∴∠DBC=∠DCB.
∵AB是直径,
∴∠ACB=90°.
∵∠ACE=25°,
∴∠DBC=∠DCB=65°,
∴∠D=180° - 65°×2=50°.故选A.
4 [2024福建宁德校级质检]如图,PA,PB是⊙O的切线,A,B为切点,点C,D在⊙O上.若∠P= 102°,则∠A+∠C= ______.
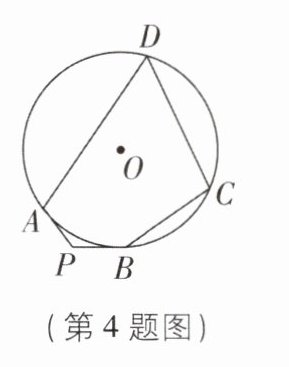

219°
答案:
219° 【解析】连接AB.
∵PA,PB是⊙O的切线,
∴PA=PB.
∵∠P=102°,
∴∠PAB=∠PBA=(1/2)(180° - 102°)=39°.
∵∠DAB+∠C=180°,
∴∠PAD+∠C=∠PAB+∠DAB+∠C=39°+180°=219°,故答案为219°.
∵PA,PB是⊙O的切线,
∴PA=PB.
∵∠P=102°,
∴∠PAB=∠PBA=(1/2)(180° - 102°)=39°.
∵∠DAB+∠C=180°,
∴∠PAD+∠C=∠PAB+∠DAB+∠C=39°+180°=219°,故答案为219°.
5 如图,⊙O内切于正方形ABCD,O为圆心,作∠MON= 90°,其两边分别交BC,CD于点N,M,若CM+CN= 4,则⊙O的面积为______.


答案:
4π 【解析】如图,设⊙O与正方形ABCD的边CD切于E,与边BC切于F,连接OE,OF,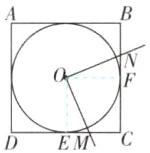
∴CF=CE=OE=OF,∠OEM=∠OFN=∠EOF=90°.
∵∠MON=90°,
∴∠EOM=∠FON,
∴△OEM≌△OFN (ASA),
∴EM=NF,
∴CM+CN=CE+CF=2CF=4,
∴OE=CF=2,
∴⊙O的面积为4π.
4π 【解析】如图,设⊙O与正方形ABCD的边CD切于E,与边BC切于F,连接OE,OF,

∴CF=CE=OE=OF,∠OEM=∠OFN=∠EOF=90°.
∵∠MON=90°,
∴∠EOM=∠FON,
∴△OEM≌△OFN (ASA),
∴EM=NF,
∴CM+CN=CE+CF=2CF=4,
∴OE=CF=2,
∴⊙O的面积为4π.
6 如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板按如图所示放置于桌面上,并量出AB= 3cm,则此光盘的直径是
6√3
cm.
答案:
6√3 【解析】设光盘的圆心为O,连接OA,OB,OC.由题意可得∠CAB=120°.
∵AB和AC与⊙O相切,
∴OC⊥AC,OB⊥AB,AB=AC.
∵AO=AO,
∴Rt△ABO≌Rt△ACO,
∴∠OAB=∠OAC=(1/2)∠CAB=60°,
∴∠AOB=30°.
∵AB=3cm,
∴OA=6cm.由勾股定理得OB = 3√3cm,
∴光盘的直径是6√3cm.故答案为6√3.
∵AB和AC与⊙O相切,
∴OC⊥AC,OB⊥AB,AB=AC.
∵AO=AO,
∴Rt△ABO≌Rt△ACO,
∴∠OAB=∠OAC=(1/2)∠CAB=60°,
∴∠AOB=30°.
∵AB=3cm,
∴OA=6cm.由勾股定理得OB = 3√3cm,
∴光盘的直径是6√3cm.故答案为6√3.
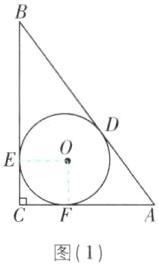
7 [2024四川自贡中考]在Rt△ABC中,∠C= 90°,⊙O是△ABC的内切圆,切点分别为D,E,F.
(1)图(1)中三组相等的线段分别是CE= CF,AF= ______,BD= ______;若AC= 3,BC= 4,则⊙O半径长为______;
(2)如图(2),延长AC到点M,使AM= AB,过点M作MN⊥AB于点N.求证:MN是⊙O的切线.

(1)图(1)中三组相等的线段分别是CE= CF,AF= ______,BD= ______;若AC= 3,BC= 4,则⊙O半径长为______;
(2)如图(2),延长AC到点M,使AM= AB,过点M作MN⊥AB于点N.求证:MN是⊙O的切线.

答案:
(1)【解】连接OE,OF,如图
(1).由切线长定理可知,AF=AD,BD=BE.
∵∠C= 90°,⊙O是△ABC的内切圆,切点分别为D,E,F,
∴∠C=∠OEC=∠OFC=90°,OE=OF,
∴四边形OECF是正方形.设OE=OF=CF=CE=x,则BE=BC - CE=4 - x=BD,AF=AC - CF=3 - x=AD.
∵BD+AD=AB=√(AC²+BC²)=√(3²+4²)=5,
∴4 - x+3 - x=5,解得x=1,
∴OE=1,即⊙O半径长为1.故答案为AD,BE,1.
(2)【证明】过O作OH⊥MN于H,连接OD,OE,如图
(2).
∵∠ANM=90°=∠ACB,∠A=∠A,AM=AB,
∴△AMN≌△ABC(AAS),
∴AN=AC.
∵AD=AF,
∴AN - AD=AC - AF,即DN=CF.由
(1)可知,CF=OE,
∴DN=OE.
∵∠ANM=90°=∠ODN=∠OHN,
∴四边形OHND是矩形,
∴OH=DN,
∴OH=OE,即OH是⊙O的半径.又
∵OH⊥MN,
∴MN是⊙O的切线.

(1)【解】连接OE,OF,如图
(1).由切线长定理可知,AF=AD,BD=BE.
∵∠C= 90°,⊙O是△ABC的内切圆,切点分别为D,E,F,
∴∠C=∠OEC=∠OFC=90°,OE=OF,
∴四边形OECF是正方形.设OE=OF=CF=CE=x,则BE=BC - CE=4 - x=BD,AF=AC - CF=3 - x=AD.
∵BD+AD=AB=√(AC²+BC²)=√(3²+4²)=5,
∴4 - x+3 - x=5,解得x=1,
∴OE=1,即⊙O半径长为1.故答案为AD,BE,1.

(2)【证明】过O作OH⊥MN于H,连接OD,OE,如图
(2).
∵∠ANM=90°=∠ACB,∠A=∠A,AM=AB,
∴△AMN≌△ABC(AAS),
∴AN=AC.
∵AD=AF,
∴AN - AD=AC - AF,即DN=CF.由
(1)可知,CF=OE,
∴DN=OE.
∵∠ANM=90°=∠ODN=∠OHN,
∴四边形OHND是矩形,
∴OH=DN,
∴OH=OE,即OH是⊙O的半径.又
∵OH⊥MN,
∴MN是⊙O的切线.

8 已知PA切⊙O于点A,PB切⊙O于点B,点C是⊙O上异于A,B的一点,过点C作⊙O的切线分别交PA和PB于点D,E,若PA= 10cm,DE= 7cm,则△PDE的周长为______cm.
答案:
20或34 【解析】分两种情况:①点C在劣弧AB上时,如图
(1).根据切线长定理得AD=CD,BE=CE,PA=PB,则△PDE的周长为PD+DE+PE=PD+CD+CE+PE=PD+AD+PE+BE=PA+PB=2PA=20cm.
②点C在优弧AB上时,如图
(2).根据切线长定理得AD=CD,BE=CE,PA=PB,则△PDE的周长为PD+DE+PE=PA+AD+CD+CE+BE+PB=2PA+2CD+2CE=2PA+2DE=2×10 + 2×7=34(cm).综上,△PDE的周长为20cm或34cm.


20或34 【解析】分两种情况:①点C在劣弧AB上时,如图
(1).根据切线长定理得AD=CD,BE=CE,PA=PB,则△PDE的周长为PD+DE+PE=PD+CD+CE+PE=PD+AD+PE+BE=PA+PB=2PA=20cm.
②点C在优弧AB上时,如图
(2).根据切线长定理得AD=CD,BE=CE,PA=PB,则△PDE的周长为PD+DE+PE=PA+AD+CD+CE+BE+PB=2PA+2CD+2CE=2PA+2DE=2×10 + 2×7=34(cm).综上,△PDE的周长为20cm或34cm.


查看更多完整答案,请扫码查看


