第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1 [2025江苏苏州质检,中]平面上有四个点,它们不都在同一直线上,过其中三个点作圆,可以作出不重复的圆 $ n $ 个,则 $ n $ 的值不可能为( )
A.4
B.3
C.2
D.1
A.4
B.3
C.2
D.1
答案:
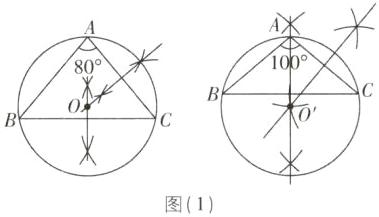
1.C [解析]分为三种情况①当四点都在同一个圆上时,如图
(1),此时n = 1.

②当三点在同一直线上时,如图
(2).分点A,B,C;A,C,D;A,B,D共圆三种情况,可作3个圆,即此时n = 3.

③当A,B,C,D四点不共圆,且其中的任何三点都不共线时,如图
(3),分点A,B,C;B,C,D;C,D,A;D,A,B共圆四种情况,可作4个圆,即此时n = 4.
综上,n的值不能是2.故选C.

1.C [解析]分为三种情况①当四点都在同一个圆上时,如图
(1),此时n = 1.

②当三点在同一直线上时,如图
(2).分点A,B,C;A,C,D;A,B,D共圆三种情况,可作3个圆,即此时n = 3.

③当A,B,C,D四点不共圆,且其中的任何三点都不共线时,如图
(3),分点A,B,C;B,C,D;C,D,A;D,A,B共圆四种情况,可作4个圆,即此时n = 4.
综上,n的值不能是2.故选C.

2 [中]如图,线段 $ AB = 6 $,$ C $ 为线段 $ AB $ 上的一个动点,分别以 $ AC $,$ BC $ 为边作等边 $ \triangle ACD $ 和等边 $ \triangle BCE $,$ \odot O $ 外接于 $ \triangle CDE $,则 $ \odot O $ 半径的最小值为( )
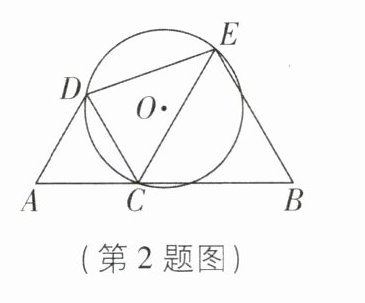
A.6
B.$ \sqrt{3} $
C.$ 2\sqrt{3} $
D.3

A.6
B.$ \sqrt{3} $
C.$ 2\sqrt{3} $
D.3
答案:
2.B [解析]如图,分别作∠DAC与∠CBE的平分线,交点为P.
∵△ACD和△BCE都是等边三角形,
∴AP与BP分别为CD,CE的垂直平分线.又
∵圆心O在CD,CE的垂直平分线上,
∴交点P与圆心O重合.连接OC.若半径OC最短,则OC⊥AB.
∵∠OAC = ∠OBC = 30°,AB = 6,
∴OA = OB,
∴AC = BC = 3,
∴在Rt△AOC中,OA = 2OC,由勾股定理得OC² = OA² - AC²,
∴3OC² = 9,
∴OC = $\sqrt{3}$,即⊙O半径的最小值为$\sqrt{3}$.故选B.

2.B [解析]如图,分别作∠DAC与∠CBE的平分线,交点为P.
∵△ACD和△BCE都是等边三角形,
∴AP与BP分别为CD,CE的垂直平分线.又
∵圆心O在CD,CE的垂直平分线上,
∴交点P与圆心O重合.连接OC.若半径OC最短,则OC⊥AB.
∵∠OAC = ∠OBC = 30°,AB = 6,
∴OA = OB,
∴AC = BC = 3,
∴在Rt△AOC中,OA = 2OC,由勾股定理得OC² = OA² - AC²,
∴3OC² = 9,
∴OC = $\sqrt{3}$,即⊙O半径的最小值为$\sqrt{3}$.故选B.

3 [2025浙江台州期中,中]半径为 $ 5\sqrt{2} $ 的 $ \odot O $ 是锐角三角形 $ ABC $ 的外接圆,$ AB = AC $,连接 $ OB $,$ OC $,延长 $ CO $ 交弦 $ AB $ 于点 $ D $。若 $ \triangle OBD $ 是直角三角形,则弦 $ BC $ 的长为______。
答案:
3.5$\sqrt{6}$或10 [解析]分两种情况①如图
(1),当∠ODB = 90°,即CD⊥AB时,AD = BD,
∴易得AC = BC.
∵AB = AC,
∴△ABC是等边三角形,
∴∠ACB = ∠ABC = 60°,
∴∠BCD = 30°.
∵OB = OC,
∴∠OBC = ∠BCD = 30°,
∴∠DBO = 30°.
∵OB = 5$\sqrt{2}$,
∴OD = $\frac{1}{2}$OB = $\frac{5\sqrt{2}}{2}$,
∴由勾股定理得BD = $\frac{5}{2}$$\sqrt{6}$,
∴BC = AB = 2BD = 5$\sqrt{6}$.

②如图
(2),当∠DOB = 90°时,∠BOC = 90°,
∴△BOC是等腰直角三角形.
∵OB = 5$\sqrt{2}$,
∴BC = $\sqrt{2}$OB = 10.故答案为5$\sqrt{6}$或10.

3.5$\sqrt{6}$或10 [解析]分两种情况①如图
(1),当∠ODB = 90°,即CD⊥AB时,AD = BD,
∴易得AC = BC.
∵AB = AC,
∴△ABC是等边三角形,
∴∠ACB = ∠ABC = 60°,
∴∠BCD = 30°.
∵OB = OC,
∴∠OBC = ∠BCD = 30°,
∴∠DBO = 30°.
∵OB = 5$\sqrt{2}$,
∴OD = $\frac{1}{2}$OB = $\frac{5\sqrt{2}}{2}$,
∴由勾股定理得BD = $\frac{5}{2}$$\sqrt{6}$,
∴BC = AB = 2BD = 5$\sqrt{6}$.

②如图
(2),当∠DOB = 90°时,∠BOC = 90°,
∴△BOC是等腰直角三角形.
∵OB = 5$\sqrt{2}$,
∴BC = $\sqrt{2}$OB = 10.故答案为5$\sqrt{6}$或10.

4 [较难]如图是一个含有 3 个正方形的相框,其中 $ \angle BCD = \angle DEF = 90^{\circ} $,$ AB = 2 $,$ CD = 3 $,$ EF = 5 $,将它镶嵌在一个圆形的金属框上,使 $ A $,$ G $,$ H $ 三点刚好在金属框上,则该金属框的半径是______。
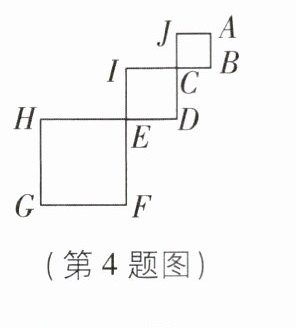

答案:
4.$\frac{5\sqrt{10}}{2}$ [解析]如图,连接AG,作线段AG和线段HG的垂直平分线交于点O,HG的垂直平分线交HG于点K,交EF于点M,连接OG,则A,G,H三点刚好在以点O为圆心,OG为半径的圆上.
∵∠BCD = ∠DEF = 90°,AB = 2,CD = 3,EF = 5,
∴AC = 2$\sqrt{2}$,EC = 3$\sqrt{2}$,EG = 5$\sqrt{2}$,
∴AG = 10$\sqrt{2}$,点E为线段AG的中点.
∵∠GEF = 45°,OE⊥AG,
∴∠OEF = 45°,
∴△OEM是等腰直角三角形,
∴MO = EM = $\frac{1}{2}$EF.
∵HG = EF = 5,
∴OK = 5 + $\frac{5}{2}$ = $\frac{15}{2}$,KG = $\frac{5}{2}$,
∴OG = $\sqrt{KG² + OK²}$ = $\sqrt{(\frac{5}{2})² + (\frac{15}{2})²}$ = $\frac{5\sqrt{10}}{2}$.故答案为$\frac{5\sqrt{10}}{2}$.

4.$\frac{5\sqrt{10}}{2}$ [解析]如图,连接AG,作线段AG和线段HG的垂直平分线交于点O,HG的垂直平分线交HG于点K,交EF于点M,连接OG,则A,G,H三点刚好在以点O为圆心,OG为半径的圆上.
∵∠BCD = ∠DEF = 90°,AB = 2,CD = 3,EF = 5,
∴AC = 2$\sqrt{2}$,EC = 3$\sqrt{2}$,EG = 5$\sqrt{2}$,
∴AG = 10$\sqrt{2}$,点E为线段AG的中点.
∵∠GEF = 45°,OE⊥AG,
∴∠OEF = 45°,
∴△OEM是等腰直角三角形,
∴MO = EM = $\frac{1}{2}$EF.
∵HG = EF = 5,
∴OK = 5 + $\frac{5}{2}$ = $\frac{15}{2}$,KG = $\frac{5}{2}$,
∴OG = $\sqrt{KG² + OK²}$ = $\sqrt{(\frac{5}{2})² + (\frac{15}{2})²}$ = $\frac{5\sqrt{10}}{2}$.故答案为$\frac{5\sqrt{10}}{2}$.

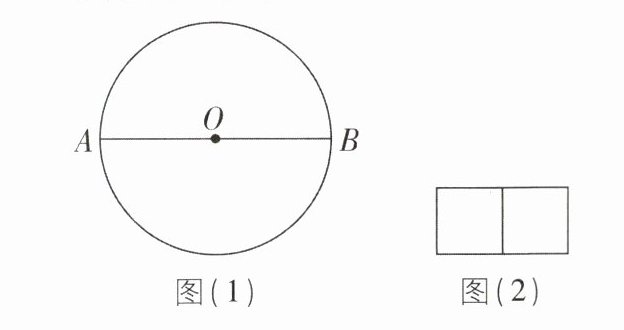
5 核心素养 模型观念 [2025江苏连云港调研,较难]定义:我们将能完全覆盖某平面图形的圆称为该平面图形的覆盖圆。其中,能完全覆盖平面图形的最小圆称为该平面图形的最小覆盖圆。例如:如图(1),线段 $ AB $ 的最小覆盖圆就是以线段 $ AB $ 为直径的圆。
【初步思考】
(1)边长为 $ 1\ \text{cm} $ 的正方形的最小覆盖圆的半径是______ $ \text{cm} $。
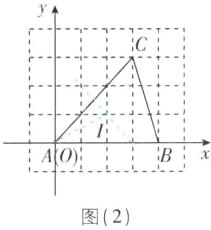
(2)如图(2),边长为 $ 1\ \text{cm} $ 的两个正方形并列在一起,则其最小覆盖圆的半径是______ $ \text{cm} $。
【深入探究】
(1)请分别作出图(3)中两个三角形的最小覆盖圆。(要求用尺规作图,保留作图痕迹,不写作法)
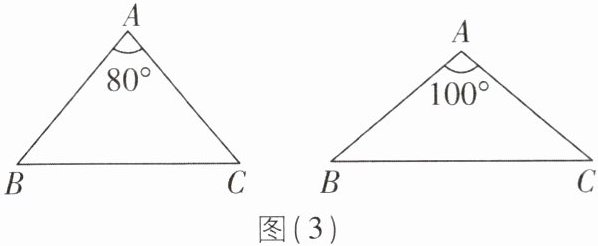
(2)如图(4),在正方形组成的网格中建立平面直角坐标系,$ \triangle ABC $ 的顶点 $ A $ 位于坐标原点,顶点 $ B $,$ C $ 的坐标分别为 $ (4,0) $,$ (3,3) $,则 $ \triangle ABC $ 的最小覆盖圆的圆心坐标为______,半径长为______;如图(5),钝角 $ \triangle MNP $ 中,$ MN = 5 $,$ \angle MPN = 123^{\circ} $,则 $ \triangle MNP $ 的最小覆盖圆的半径长为______。
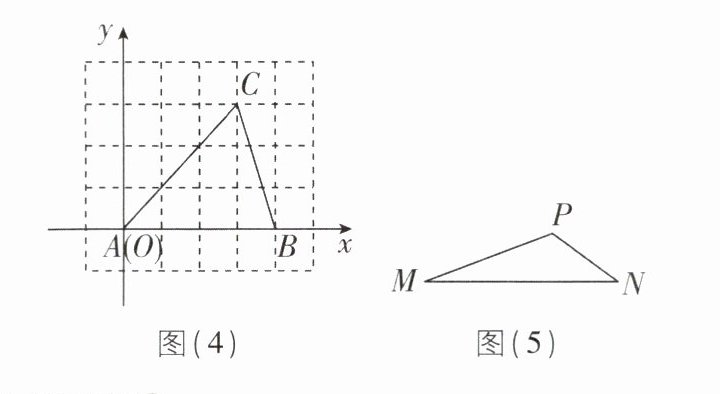
【生活应用】
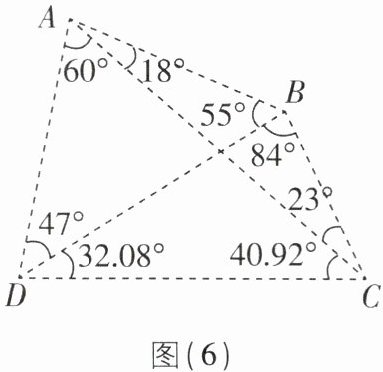
某地有四个村庄 $ A $,$ B $,$ C $,$ D $(其位置如图(6)所示),现拟建一个 5G 网络信号中转站,为了使这四个村庄的居民都能接收到信号,经过工程人员测量得到 $ CD = 8\ \text{km} $ 及图中标注的相关数据,则四边形 $ ABCD $ 区域最小覆盖圆的半径为______。

【初步思考】
(1)边长为 $ 1\ \text{cm} $ 的正方形的最小覆盖圆的半径是______ $ \text{cm} $。
(2)如图(2),边长为 $ 1\ \text{cm} $ 的两个正方形并列在一起,则其最小覆盖圆的半径是______ $ \text{cm} $。
【深入探究】
(1)请分别作出图(3)中两个三角形的最小覆盖圆。(要求用尺规作图,保留作图痕迹,不写作法)

(2)如图(4),在正方形组成的网格中建立平面直角坐标系,$ \triangle ABC $ 的顶点 $ A $ 位于坐标原点,顶点 $ B $,$ C $ 的坐标分别为 $ (4,0) $,$ (3,3) $,则 $ \triangle ABC $ 的最小覆盖圆的圆心坐标为______,半径长为______;如图(5),钝角 $ \triangle MNP $ 中,$ MN = 5 $,$ \angle MPN = 123^{\circ} $,则 $ \triangle MNP $ 的最小覆盖圆的半径长为______。

【生活应用】
某地有四个村庄 $ A $,$ B $,$ C $,$ D $(其位置如图(6)所示),现拟建一个 5G 网络信号中转站,为了使这四个村庄的居民都能接收到信号,经过工程人员测量得到 $ CD = 8\ \text{km} $ 及图中标注的相关数据,则四边形 $ ABCD $ 区域最小覆盖圆的半径为______。

答案:
5.[解][初步思考]
(1)
∵正方形的边长为1 cm,
∴由勾股定理得正方形的对角线长为$\sqrt{2}$ cm,
∴最小覆盖圆的半径是$\frac{\sqrt{2}}{2}$ cm.故答案为$\frac{\sqrt{2}}{2}$.
(2)由题意得,矩形的长为2 cm,宽为1 cm,
∴由勾股定理得矩形的对角线长为$\sqrt{5}$ cm,
∴最小覆盖圆的半径是$\frac{\sqrt{5}}{2}$ cm.故答案为$\frac{\sqrt{5}}{2}$.
[深入探究]
(1)如图
(1)所示,圆O和圆O'即为所作.
(2)如图
(2),AB和AC垂直平分线的交点为I(2,1),
∴OI = $\sqrt{2² + 1²}$ = $\sqrt{5}$,即△ABC的最小覆盖圆的圆心坐标为(2,1),半径长为$\sqrt{5}$.由题意得,MN的长为△MPN最小覆盖圆的直径.令△MPN最小覆盖圆的圆心为F.
∵MN = 5,
∴FM = FN = $\frac{5}{2}$,
∴△MNP的最小覆盖圆的半径是$\frac{5}{2}$.故答案为(2,1),$\sqrt{5}$,$\frac{5}{2}$.
[生活应用]如图
(3),作△ADC的外接圆⊙O.
∵△ADC的最小覆盖圆⊙O可以将四边形ABCD覆盖,
∴四边形ABCD的最小覆盖圆是△ACD的外接圆.作直径DE,连接CE,则∠DCE = 90°.
∵$\overset{\frown}{CD}$ = $\overset{\frown}{CD}$,
∴∠E = ∠DAC = 60°,
∴∠EDC = 30°.在Rt△DCE中,DE = 2CE,CD = 8 km,由勾股定理得DE² = CE² + CD²,即(2CE)² = CE² + 8²,
∴3CE² = 64,
∴CE = $\frac{8}{3}$$\sqrt{3}$ km,
∴DE = $\frac{16}{3}$$\sqrt{3}$ km,
∴四边形ABCD区域最小覆盖圆的半径为$\frac{8}{3}$$\sqrt{3}$ km.故答案为$\frac{8}{3}$$\sqrt{3}$ km.

5.[解][初步思考]
(1)
∵正方形的边长为1 cm,
∴由勾股定理得正方形的对角线长为$\sqrt{2}$ cm,
∴最小覆盖圆的半径是$\frac{\sqrt{2}}{2}$ cm.故答案为$\frac{\sqrt{2}}{2}$.
(2)由题意得,矩形的长为2 cm,宽为1 cm,
∴由勾股定理得矩形的对角线长为$\sqrt{5}$ cm,
∴最小覆盖圆的半径是$\frac{\sqrt{5}}{2}$ cm.故答案为$\frac{\sqrt{5}}{2}$.
[深入探究]
(1)如图
(1)所示,圆O和圆O'即为所作.

(2)如图
(2),AB和AC垂直平分线的交点为I(2,1),
∴OI = $\sqrt{2² + 1²}$ = $\sqrt{5}$,即△ABC的最小覆盖圆的圆心坐标为(2,1),半径长为$\sqrt{5}$.由题意得,MN的长为△MPN最小覆盖圆的直径.令△MPN最小覆盖圆的圆心为F.
∵MN = 5,
∴FM = FN = $\frac{5}{2}$,
∴△MNP的最小覆盖圆的半径是$\frac{5}{2}$.故答案为(2,1),$\sqrt{5}$,$\frac{5}{2}$.

[生活应用]如图
(3),作△ADC的外接圆⊙O.
∵△ADC的最小覆盖圆⊙O可以将四边形ABCD覆盖,
∴四边形ABCD的最小覆盖圆是△ACD的外接圆.作直径DE,连接CE,则∠DCE = 90°.
∵$\overset{\frown}{CD}$ = $\overset{\frown}{CD}$,
∴∠E = ∠DAC = 60°,
∴∠EDC = 30°.在Rt△DCE中,DE = 2CE,CD = 8 km,由勾股定理得DE² = CE² + CD²,即(2CE)² = CE² + 8²,
∴3CE² = 64,
∴CE = $\frac{8}{3}$$\sqrt{3}$ km,
∴DE = $\frac{16}{3}$$\sqrt{3}$ km,
∴四边形ABCD区域最小覆盖圆的半径为$\frac{8}{3}$$\sqrt{3}$ km.故答案为$\frac{8}{3}$$\sqrt{3}$ km.

查看更多完整答案,请扫码查看


