《2025年初中必刷题九年级数学上册苏科版》

1 [中]如图,在$\odot O$中,弦$AB = 5$,点 C 在 AB 上移动,连接 OC,过点 C 作$CD⊥OC交\odot O$于点 D,则 CD 的最大值为 (B)

A.5
B.2.5
C.3
D.2

答案： B 【解析】连接 OD.设⊙O 的半径为 r.
∵ CD⊥OC，
∴ ∠DCO = 90°，
∴ CD = $\sqrt{OD^2 - OC^2} = \sqrt{r^2 - OC^2}$，
∴ 当 OC 的值最小时，CD 的值最大.当 OC⊥AB 时，OC 最小，此时 D，B 两点重合，
∴ CD = CB = $\frac{1}{2}$AB = $\frac{1}{2}×5 = 2.5$，即 CD 的最大值为 2.5，故选 B.

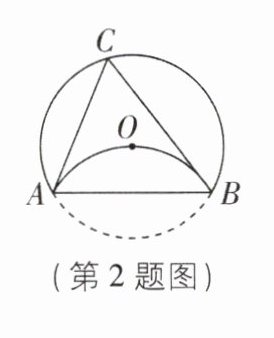
2 [2024 江苏无锡质检,中]如图,$\odot O$的半径为 4,将劣弧沿弦 AB 翻折,恰好经过圆心 O,点 C 为优弧$\overset{\frown}{AB}$上的一个动点,则$\triangle ABC$面积的最大值是 ( )


A.$12\sqrt{3}$
B.$12\sqrt{2}$
C.$4\sqrt{3}$
D.$8 + 8\sqrt{2}$

答案：
A 【解析】如图，过点 O 作 OM⊥AB 于 H，交弧 AB 于点 M，连接 AO，CO.当点 C 运动到优弧$\overset{\frown}{AB}$中点时，C，O，H 三点共线，△ABC 中，以 AB 为底，高为 CO + OH，此时△ABC 的面积最大.
∵ 点 C 运动到优弧$\overset{\frown}{AB}$中点，
∴ CH⊥AB，且 AH = HB.
∵ 将劣弧沿弦 AB 翻折，恰好经过圆心 O，
∴ OH = HM.
∵⊙O 的半径为 4，
∴ OH = HM = $\frac{1}{2}$OM = 2，CO = AO = 4，
∴ 在 Rt△AOH 中，利用勾股定理得 AH = $\sqrt{AO^2 - OH^2} = \sqrt{4^2 - 2^2} = 2\sqrt{3}$，
∴ AB = 2AH = $4\sqrt{3}$.
∵ CH = CO + OH = 6，
∴$S_{\triangle ABC} = \frac{1}{2}AB·CH = \frac{1}{2}×4\sqrt{3}×6 = 12\sqrt{3}$.故选 A.

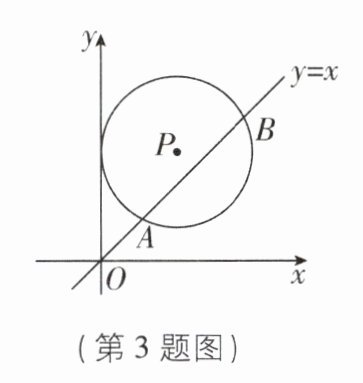
3 [较难]如图,在平面直角坐标系中,$\odot P的圆心坐标是(3,a)(a ＞ 3)$,半径为 3,函数$y = x的图像被\odot P$截得的弦 AB 的长为$4\sqrt{2}$,则 a 的值是 ( )


A.$2\sqrt{3}$
B.$2 + \sqrt{2}$
C.$2 - \sqrt{2}$
D.$3 + \sqrt{2}$

答案：
D 【解析】过点 P 作 PC⊥x 轴于点 C，交 AB 于点 D，作 PE⊥AB 于点 E，连接 PB，如图.
∵⊙P 的圆心坐标是（3，a），
∴ OC = 3，PC = a.把 x = 3 代入 y = x 得 y = 3，
∴ 点 D 的坐标为（3，3），
∴ CD = 3，
∴ △OCD 为等腰直角三角形，
∴ △PED 也为等腰直角三角形.
∵ PE⊥AB，
∴ AE = BE = $\frac{1}{2}$AB = $2\sqrt{2}$.在 Rt△PBE 中，PB = 3，
∴ PE = $\sqrt{PB^2 - BE^2} = \sqrt{3^2 - (2\sqrt{2})^2} = 1$，
∴ PD = $\sqrt{PE^2 + DE^2} = \sqrt{2}PE = \sqrt{2}$，
∴ a = 3 + $\sqrt{2}$.故选 D.

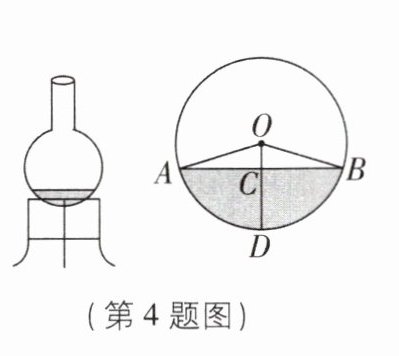
4 新考法[中]如图,一个底部呈球形的烧瓶,球的半径为 5 cm,瓶内原有液体的最大深度$CD = 4$cm. 部分液体蒸发后,瓶内液体的最大深度下降为 2 cm,则截面圆中弦 AB 的长减少了______cm(结果保留根号).

答案：
$(4\sqrt{6} - 8)$ 【解析】如图，A'B'//AB，设 A'B'交 OD 于 E，连接 OA'.由题意得 OA = OA' = OD = 5 cm，OD⊥AB，OD⊥A'B'，
∴ AC = BC，A'E = B'E.
∵ CD = 4 cm，
∴ OC = OD - CD = 1 cm，
∴ AC = $\sqrt{OA^2 - OC^2} = \sqrt{5^2 - 1^2} = 2\sqrt{6}$（cm），
∴ AB = 2AC = $4\sqrt{6}$ cm.
∵ DE = 2 cm，
∴ OE = OD - DE = 3 cm，
∴ A'E = $\sqrt{OA'^2 - OE^2} = \sqrt{5^2 - 3^2} = 4$（cm），
∴ A'B' = 2A'E = 8 cm，
∴ AB - A'B' = $(4\sqrt{6} - 8)$cm，即截面圆中弦 AB 的长减少了$(4\sqrt{6} - 8)$cm，故答案为$(4\sqrt{6} - 8)$.

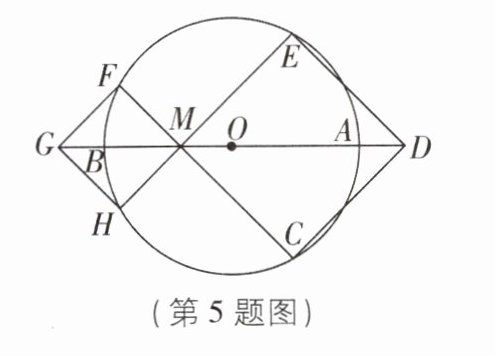
5 [2025 浙江温州调研,中]如图,点 M 在$\odot O$的直径 AB 上,作正方形 MCDE 和正方形 MFGH,其中点 D,G 在直径 AB 所在直线上,点 C,E,F,H 都在$\odot O$上,若两个正方形的面积之和为 2a,$OM = \sqrt{2}$,则$FM\cdot MC$的值是______.(用含 a 的代数式表示)

答案：
a - 2 【解析】作 OK⊥FC 于 K，如图.设正方形 MFGH 的边长是 x.
∵ 四边形 MCDE 是正方形，
∴ ∠CMD = 45°.
∵ ∠OKM = 90°，
∴ △KOM 是等腰直角三角形，
∴ MK = $\frac{\sqrt{2}}{2}$OM = $\frac{\sqrt{2}}{2}×\sqrt{2} = 1$.
∵ OK⊥CF，
∴ CK = FK = x + 1，
∴ MC = CK + MK = x + 2.
∵ 两个正方形的面积之和为 2a，
∴$x^2 + (x + 2)^2 = 2a$，化简得$x^2 + 2x = a - 2$，
∴ x(x + 2) = a - 2，
∴ FM·CM = x(x + 2) = a - 2.故答案为 a - 2.

6 新考法[2024 湖北黄冈质检,中]如图,在半径为 1 的$\odot O$中有三条弦 AB,CD,EF,它们所对的圆心角分别为$60^{\circ},90^{\circ},120^{\circ}$,那么以这三条弦长为边长的三角形的面积是______.

答案：
$\frac{\sqrt{2}}{2}$ 【解析】如图，连接 OA，OB，OC，OD，OE，OF，则∠AOB = 60°，∠COD = 90°，∠EOF = 120°.在 Rt△COD 中，CD = $\sqrt{1^2 + 1^2} = \sqrt{2}$.
∵ OA = OB，∠AOB = 60°，
∴ △AOB 是等边三角形，
∴ AB = OA = 1.过点 O 作 OH⊥EF 于点 H，则 FH = EH，∠EOH = ∠FOH = 60°，
∴ ∠F = 30°，
∴ OH = $\frac{1}{2}$，
∴ FH = $\frac{\sqrt{3}}{2}$，
∴ EF = 2FH = $\sqrt{3}$.
∵$1^2 + (\sqrt{2})^2 = (\sqrt{3})^2$，即$AB^2 + CD^2 = EF^2$，
∴ 以 AB，CD，EF 为边的三角形为直角三角形，
∴ 其面积为$\frac{1}{2}×\sqrt{2}×1 = \frac{\sqrt{2}}{2}$.故答案为$\frac{\sqrt{2}}{2}$.

7 新考法[2025 江苏南京调研,较难]如图,已知两个半径不同的圆,请用直尺与圆规按下列要求完成作图.
(1)请分别画出两个圆的直径.
(2)请画出一个圆使得它的面积等于已知两个圆面积的和.

答案：
（1）如图（1）所示.

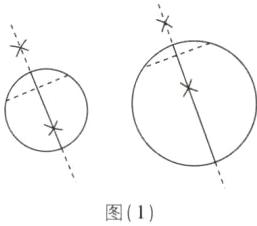
（2）如图（2）所示，以 r 为半径的大圆即为所求.

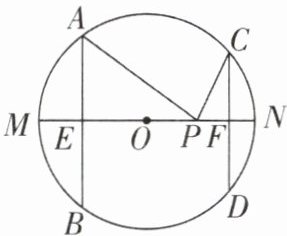
8 [较难]如图,AB,CD 是半径为 5 的$\odot O$的两条弦,MN 为直径,$AB = 8,CD = 6,AB⊥MN$于 E,$CD⊥MN$于 F.
(1)求 EF 的长.
(2)若点 P 在直径 MN 上运动,试求$PA + PC$的最小值.

答案：
（1）如图，连接 OB，OC.
∵ AB = 8，CD = 6，MN 是直径，AB⊥MN 于点 E，CD⊥MN 于点 F，
∴ BE = $\frac{1}{2}$AB = 4，CF = $\frac{1}{2}$CD = 3，
∴ OE = $\sqrt{OB^2 - BE^2} = \sqrt{5^2 - 4^2} = 3$，OF = $\sqrt{OC^2 - CF^2} = 4$，
∴ EF = OE + OF = 7.
（2）如图，作 CH⊥AB 于 H，连接 BC，BP.由于 A，B 两点关于 MN 对称，因而 PA+PC = PB+PC，则当 B，C，P 在同一条直线上时，PA+PC 的值最小，即 BC 的值就是 PA+PC 的最小值.
∵ AB⊥MN 于 E，CD⊥MN 于 F，CH⊥AB，
∴ ∠CHE = ∠HEF = ∠CFE = 90°，
∴ 四边形 CHEF 是矩形，
∴ CH = EF = 7，EH = CF = 3，
∴ BH = BE + EH = 4 + 3 = 7.在 Rt△BCH 中，根据勾股定理得到 BC = $\sqrt{BH^2 + CH^2} = \sqrt{7^2 + 7^2} = 7\sqrt{2}$，即 PA+PC 的最小值为$7\sqrt{2}$.