《2025年初中必刷题九年级数学上册苏科版》

1 [2025 浙江绍兴期末] 甲、乙两人同时从同一地点出发,甲的速度为每秒 1.5 米,乙的速度为每秒 1 米,乙一直向东走,甲先向南走 10 米,然后又朝北偏东某个方向走了一段后与乙相遇,则乙走了______米。
24

答案： 24 【解析】设甲、乙两人走了x秒，则乙走的路程为x米，甲在北偏东某个方向走的路程为(1.5x - 10)米。由题意，得(1.5x - 10)² = 10² + x²，解得x = 24或x = 0(舍去)，
∴ 乙走的路程为24米，故答案为24。

如图,在等腰 $\text{Rt}\triangle ABC $ 中, $ AB = BC = 8\ \text{cm} $,动点 $ P $ 从 $ A $ 点出发,沿 $ AB $ 向 $ B $ 移动。过点 $ P $ 作平行于 $ BC $,$ AC $ 的直线,分别与 $ AC $,$ BC $ 交于点 $ R $,$ Q $。当动点 $ P $ 从 $ A $ 点出发移动4 $ \text{cm} $ 时,$ □ PQCR $ 的面积等于 $ 16\ \text{cm}^2 $。

答案： 4 【解析】设动点P从A点出发移动x cm时，▱PQCR的面积等于16 cm²，则AP = x cm，BP = (8 - x)cm。
∵ △ABC是等腰直角三角形，PR // BC，
∴ △APR是等腰直角三角形，
∴ PR = AP = x cm。依题意得x(8 - x) = 16，解得x₁ = x₂ = 4。故答案为4。

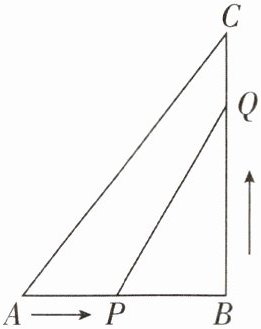
3 [2025 广东广州调研] 如图,在 $ \triangle ABC $ 中,$ \angle B = 90^{\circ} $,$ AB = 5\ \text{cm} $,$ BC = 7\ \text{cm} $,点 $ P $ 从点 $ A $ 开始沿 $ AB $ 边向终点 $ B $ 以 $ 1\ \text{cm/s} $ 的速度移动,点 $ Q $ 从点 $ B $ 开始沿 $ BC $ 边向终点 $ C $ 以 $ 2\ \text{cm/s} $ 的速度移动。当 $ P $,$ Q $ 两点中有一点到达终点时,两点同时停止移动。
(1)如果 $ P $,$ Q $ 分别从 $ A $,$ B $ 同时出发,那么几秒后,$ \triangle PBQ $ 的面积等于 $ 4\ \text{cm}^2 $？
(2)如果 $ P $,$ Q $ 分别从 $ A $,$ B $ 同时出发,那么几秒后,$ PQ $ 的长度等于 $ 5\ \text{cm} $？
(3)在(1)中,$ \triangle PBQ $ 的面积能否等于 $ 8\ \text{cm}^2 $？说明理由。

答案： 【解】
(1)设经过x s后，△PBQ面积为4 cm²，此时AP = x cm，BQ = 2x cm，则BP = (5 - x)cm。由$\frac{1}{2}$BP·BQ = 4，得$\frac{1}{2}$(5 - x)×2x = 4，整理得x² - 5x + 4 = 0，解得x = 1或x = 4(不合题意，舍去)，
∴ 1 s后，△PBQ的面积等于4 cm²。
(2)设经过t s后，PQ的长度等于5 cm。由勾股定理得PQ² = BP² + BQ²，即25 = (5 - t)² + (2t)²，解得t₁ = 0，t₂ = 2，
∴ 0 s或2 s后，PQ的长度等于5 cm。
(3)不能，理由如下：由题意，得$\frac{1}{2}$(5 - x)×2x = 8，整理得x² - 5x + 8 = 0。
∵ (-5)² - 4×1×8 = 25 - 32 = -7 ＜ 0，
∴ 该方程没有实数根，
∴ △PQB的面积不能等于8 cm²。

4 [2024 江苏泰州期中] 如图,在矩形 $ ABCD $ 中, $ AB = 3\sqrt{2}\ \text{cm} $,$ BC = \sqrt{2}\ \text{cm} $,点 $ P $ 从点 $ A $ 出发沿 $ AB $ 以 $ \sqrt{2}\ \text{cm/s} $ 的速度向点 $ B $ 运动,当 $ PA = \sqrt{2}PC $ 时,点 $ P $ 运动的时间为(B)
A.$ \sqrt{2}\ \text{s} $
B.$ 2\ \text{s} $
C.$ 10\ \text{s} $
D.$ 10\ \text{s} $ 或 $ 2\ \text{s} $

答案： B 【解析】设点P运动的时间为t s。根据题意得AP = $\sqrt{2}$t cm，
∴ PC = $\frac{\sqrt{2}t}{\sqrt{2}}$ = t cm。
∵ PB = AB - AP = (3$\sqrt{2}$ - $\sqrt{2}$t)cm，PC² = BC² + PB²，
∴ t² = ($\sqrt{2}$)² + (3$\sqrt{2}$ - $\sqrt{2}$t)²，解得t = 2或t = 10(不合题意，舍去)，
∴ 点P运动的时间为2 s，故选B。

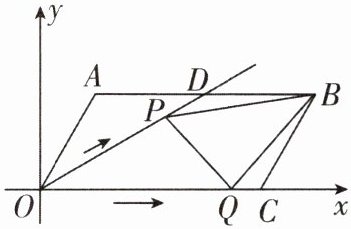
5 如图,点 $ O $ 为坐标原点,点 $ C $ 在 $ x $ 轴的正半轴上。在 $ □ AOCB $ 中,边 $ AO = 2 $,$ OC = 4 $,$ \angle AOC = 60^{\circ} $,$ \angle AOC $ 的平分线交 $ AB $ 于点 $ D $。
(1)求 $ B $,$ D $ 两点的坐标；
(2)点 $ P $ 从点 $ O $ 出发,以每秒 $ \sqrt{3} $ 个单位长度的速度沿射线 $ OD $ 方向移动；同时点 $ Q $ 从点 $ O $ 出发,以每秒 $ 2 $ 个单位长度的速度沿射线 $ OC $ 方向移动。连接 $ QP $,$ BQ $,$ BP $,设移动时间为 $ t $ 秒。当 $ t $ 为何值时,$ \triangle PQB $ 是直角三角形。

答案： 【解】
(1)作AH⊥OC于H。在Rt△AOH中，
∵ ∠AOH = 60°，
∴ ∠OAH = 30°。
∵ OA = 2，
∴ OH = $\frac{1}{2}$OA = 1，
∴ AH = $\sqrt{3}$，
∴ A(1, $\sqrt{3}$)。
∵ 四边形AOCB是平行四边形，
∴ AB = OC = 4，AB // OC，
∴ B(5, $\sqrt{3}$)，∠ADO = ∠DOC。
∵ OD平分∠AOC，
∴ ∠AOD = ∠DOC，
∴ ∠AOD = ∠ADO，
∴ AO = AD = 2，
∴ D(3, $\sqrt{3}$)。综上，B、D两点的坐标分别为(5, $\sqrt{3}$)，(3, $\sqrt{3}$)。
(2)由题意易得P($\frac{3}{2}$t, $\frac{\sqrt{3}}{2}$t)，Q(2t, 0)，
∴ PB² = ($\frac{3}{2}$t - 5)² + ($\frac{\sqrt{3}}{2}$t - $\sqrt{3}$)²，BQ² = (5 - 2t)² + 3，PQ² = ($\frac{1}{2}$t)² + ($\frac{\sqrt{3}}{2}$t)²。①当PB为斜边时，($\frac{3}{2}$t - 5)² + ($\frac{\sqrt{3}}{2}$t - $\sqrt{3}$)² = (5 - 2t)² + 3 + ($\frac{1}{2}$t)² + ($\frac{\sqrt{3}}{2}$t)²，解得t = 1或t = 0(舍去)；②当PQ为斜边时，($\frac{3}{2}$t - 5)² + ($\frac{\sqrt{3}}{2}$t - $\sqrt{3}$)² + (5 - 2t)² + 3 = ($\frac{1}{2}$t)² + ($\frac{\sqrt{3}}{2}$t)²，解得t = 4或t = $\frac{7}{3}$；③当BQ为斜边时，($\frac{3}{2}$t - 5)² + ($\frac{\sqrt{3}}{2}$t - $\sqrt{3}$)² + ($\frac{1}{2}$t)² + ($\frac{\sqrt{3}}{2}$t)² = (5 - 2t)² + 3，解得t = 0(舍去)。综上所述，当t的值为1或4或$\frac{7}{3}$时，△PQB是直角三角形。