《2025年初中必刷题九年级数学上册苏科版》

1 [2025江苏扬州质检,中]已知关于x的一元二次方程$ax^{2}+bx+c= 0$,若$a-b+c= 0$,则此方程必有一个根为(C)
A.1
B.0
C.-1
D.-2

答案： C 【解析】将x=-1代入方程ax²+bx+c=0，得a-b+c=0，
∴x=-1是方程ax²+bx+c=0的一个根.故选C.

若$x_{1}是方程ax^{2}-4x-c= 0(a≠0)$的一个根,设$p= (ax_{1}-2)^{2}$,$q= ac+5$,则p与q的大小关系为(A)
A.$p＜q$
B.$p= q$
C.$p＞q$
D.不能确定

答案： A 【解析】
∵x₁是方程ax²-4x-c=0(a≠0)的一个根，
∴ax₁²-4x₁=c，则p-q=(ax₁-2)²-(ac+5)=a²x₁²-4ax₁+4-ac-5=a(ax₁²-4x₁)-ac-1=ac-ac-1=-1，
∴p-q＜0，
∴p＜q.故选A.

若关于x的一元二次方程$ax^{2}-bx= c(ac≠0)$的一个实数根为2024,则方程$cx^{2}+bx= a(ac≠0)$一定有实数根(D)
A.2024
B.$-\frac {1}{2024}$
C.-2024
D.$\frac {1}{2024}$

答案： D 【解析】
∵关于x的一元二次方程ax²-bx=c(ac≠0)的一个实数根为2024，
∴2024²a-2024b=c，
∴a-b/2024=c/2024²，
∴c/2024²+b/2024=a，
∴(1/2024)²c+1/2024b=a，
∴x=1/2024是方程cx²+bx=a(ac≠0)的一个实数根，故选D.

已知方程$x^{2}+2x-3= 0的根是x_{1}= 1,x_{2}= -3$,则方程$(2x+3)^{2}+2(2x+3)-3= 0$的根是(C)
A.-1或3
B.1或3
C.-1或-3
D.1或-3

答案： C 【解析】
∵方程x²+2x-3=0的根是x₁=1，x₂=-3，
∴(2x+3)²+2(2x+3)-3=0的根为2x+3=1或2x+3=-3，
∴x=-1或x=-3，故选C.

5 [2024浙江金华调研,中]已知m为方程$x^{2}+3x-2023= 0$的根,则$m^{3}+2m^{2}-2026m-2023$的值为____-4046.

答案： -4046 【解析】
∵m为方程x²+3x-2023=0的根，
∴m²+3m-2023=0，
∴m²=-3m+2023，-m²-3m=-2023，
∴m³=m(-3m+2023)=-3m²+2023m，
∴m³+2m²-2026m-2023=-3m²+2023m+2m²-2026m-2023=-m²-3m-2023=-2023-2023=-4046.故答案为-4046.

6 新考向传统文化[2025江苏连云港期中,中]小明同学是一位古诗文的爱好者,在学习了一元二次方程这一章后,改编了诗词《念奴娇·赤壁怀古》:“大江东去浪淘尽,千古风流人物. 而立之年督东吴,早逝英年两位数. 十位恰小个位三,个位平方与寿同. 哪位学子算得快,多少年华数周瑜?”假设周瑜去世时年龄的十位数字是x,则可列方程为10x+(x+3)=(x+3)².

答案： 10x+(x+3)=(x+3)² 【解析】：周瑜去世时年龄的十位数字是x，
∴个位上的数字是(x+3).由题意可得10x+(x+3)=(x+3)².故答案为10x+(x+3)=(x+3)².

7 [2024辽宁沈阳皇姑区质检,中]如图都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第n个图形共有210个小球,则可列方程为n(n+1)/2=210.

答案： n(n+1)/2=210 【解析】第1个图形中有1个小球；第2个图形中有3个小球，3=1+2；第3个图形中有6个小球，6=1+2+3；第4个图形中有10个小球，10=1+2+3+4；…；照此规律，第n个图形中有1+2+3+…+n=n(n+1)/2（个）小球.由第n个图形共有210个小球可得n(n+1)/2=210，故答案为n(n+1)/2=210.

8 [2024江苏苏州期中,中]若m是一元二次方程$x^{2}-3x+1= 0$的一个根,则代数式$m-\frac {1}{m}$的值为±√5.

答案： ±√5 【解析】
∵m是一元二次方程x²-3x+1=0的一个根，
∴m²-3m+1=0，且m≠0，
∴m-3+1/m=0，
∴m+1/m=3，
∴(m+1/m)²=9，即m²+2+1/m²=9，
∴m²-2+1/m²=5，
∴(m-1/m)²=5，
∴m-1/m=±√5.故答案为±√5.

9 [2025江苏南京调研,中]如图,一块长方形绿地长10 m,宽5 m,在绿地中开辟三条宽为x m的道路后,绿地面积缩小到原来的78%,则可列方程为__(10-2x)(5-x)=10×5×78%__.

答案： (10-2x)(5-x)=10×5×78% 【解析】由题意，得(10-2x)(5-x)=10×5×78%，故答案为(10-2x)(5-x)=10×5×78%.

10 思想方法数形结合[2025江苏南通调研,较难]如图所示,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是$Rt△ABC和Rt△BED$的边长,易知$AE= \sqrt {2}c$,这时我们把关于x的形如$ax^{2}+\sqrt {2}cx+b= 0$的一元二次方程称为“勾系一元二次方程”. 请解决下列问题:
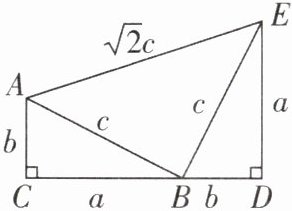
(1)试判断方程$x^{2}+2x+1= 0$是否为“勾系一元二次方程”.
(2)若$x= -1$是“勾系一元二次方程”$ax^{2}+\sqrt {2}cx+b= 0$的一个根,且四边形ACDE的周长是12,求$△ABC$的面积.

答案： 【解】（1）根据定义，方程x²+2x+1=0变形为x²+√2×√2x+1=0，得到a=1，b=1，c=√2.
∵a²+b²=c²，
∴方程x²+2x+1=0是“勾系一元二次方程”.（2）
∵x=-1是“勾系一元二次方程”ax²+√2cx+b=0的一个根，
∴a-√2c+b=0，
∴a+b=√2c.
∵四边形ACDE的周长是12，
∴2a+2b+√2c=12，
∴a+b=4，
∴4=√2c，
∴c=2√2，
∴a²+b²=c²=8.
∵(a+b)²=a²+b²+2ab，
∴(a+b)²-(a²+b²)/2=ab=4，
∴1/2ab=2，
∴S△ABC=1/2ab=2.故△ABC的面积为2.