《2025年初中必刷题九年级数学上册苏科版》

1 [2025 江苏徐州质检]下列命题中,正确的是 (D)
A.平分弦的直线必垂直于这条弦
B.垂直于弦的直线必过圆心
C.平分弦的直径必垂直于这条弦,并且平分这条弦所对的两条弧
D.垂直平分弦的直线必平分这条弦所对的弧

答案： D 【解析】过弦的中点的直线都是平分弦的直线，有无数条，所以平分弦的直线不一定垂直于这条弦，故 A 错误.垂直于弦的直线有无数条，所以垂直于弦的直线不一定过圆心，垂直平分弦的直线才过圆心，故 B 错误.根据垂径定理的推论，平分弦（不是直径）的直径必垂直于这条弦，并且平分这条弦所对的两条弧，故 C 错误.垂直平分弦的直线必过圆心，并且平分这条弦所对的弧，故 D 正确.故选 D.

如图,在$\odot O$中,弦 AB 的长为 4,圆心到弦 AB 的距离 OC 为 2,则$\odot O$的半径长是 (C)
A.1
B.$\sqrt{2}$
C.$2\sqrt{2}$
D.4

答案： C 【解析】
∵ 圆心到弦 AB 的距离 OC 为 2，
∴ OC⊥AB.
∵ 弦 AB 的长为 4，
∴ AC=$\frac{1}{2}$AB = 2，
∴ OA = $\sqrt{AC^2 + OC^2} = 2\sqrt{2}$，即⊙O 的半径长是$2\sqrt{2}$，故选 C.

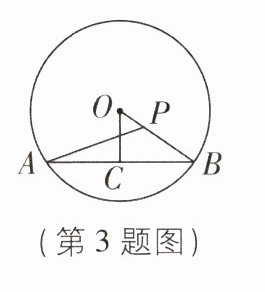
3 如图,AB 是$\odot O$的弦,$OC⊥AB$于点 C,连接 OB,点 P 是半径 OB 上任意一点,连接 AP,若$OB = 5,OC = 3$,则 AP 的长不可能是 ( )


A.6
B.7
C.8
D.9

答案：
D 【解析】如图，连接 OA.
∵ OC⊥AB 于点 C，OB = 5，OC = 3，
∴ OA = OB = 5，BC = $\sqrt{5^2 - 3^2} = 4$，
∴ AB = 2×4 = 8.
∵ AO≤AP≤AB，
∴ 5≤AP≤8，
∴ AP 的长不可能是 9.故选 D.

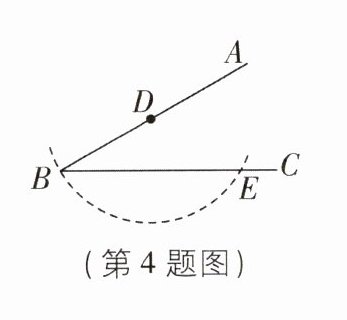
4 如图,$∠ABC = 30^{\circ}$,边 BA 上有一点 D,$DB = 6$,以点 D 为圆心,DB 长为半径作弧交 BC 于点 E,则 BE 的长是 ( )


A.$3\sqrt{3}$
B.6
C.$6\sqrt{3}$
D.12

答案：
C 【解析】如图，过点 D 作 DF⊥BC 于 F，则 BE = 2BF，∠BFD = 90°.在 Rt△BFD 中，∠ABC = 30°，BD = 6，
∴ DF = $\frac{1}{2}$BD = 3，
∴ BF = $\sqrt{BD^2 - DF^2} = 3\sqrt{3}$，
∴ BE = 2BF = $6\sqrt{3}$.故选 C.

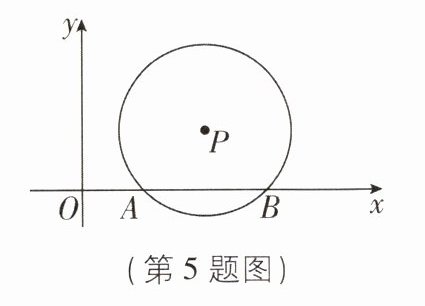
5 [2024 江苏扬州质检]如图,以点 P 为圆心的圆与 x 轴交于 A,B 两点,点 P 的坐标为$(4,2)$,点 A 的坐标为$(2,0)$,则点 B 的坐标为______.

答案：
（6，0）【解析】如图，过点 P 作 PC⊥AB 于点 C.
∵ 以点 P 为圆心的圆与 x 轴交于 A，B 两点，
∴ AC = BC.
∵ 点 P 的坐标为（4，2），点 A 的坐标为（2，0），
∴ 点 C 的坐标为（4，0），AC = 2，
∴ BC = 2，
∴ OB = 6，
∴ 点 B 的坐标为（6，0）.故答案为（6，0）.

6 [2024 江苏无锡期末]P 为平面上一点,$OP = 4$,$\odot O$半径为 5,则经过 P 点的最短弦长为______.

答案：
6 【解析】
∵ OP = 4 ＜ 5，
∴ 点 P 在⊙O 内.如图，过 P 作 AB⊥OP，交⊙O 于 A，B，则线段 AB 是过 P 点的最短的弦，连接 OA.
∵ ∠OPA = 90°，
∴ 由勾股定理得 AP = $\sqrt{OA^2 - OP^2} = \sqrt{5^2 - 4^2} = 3$.
∵ OP⊥AB，OP 过圆心 O，
∴ BP = AP = 3，
∴ AB = 2AP = 6，故答案为 6.

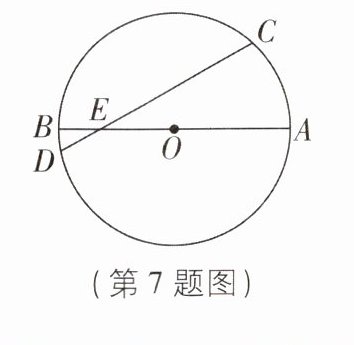
7 [2024 江苏常州期中]如图,AB 是$\odot O$的直径,弦 CD 交 AB 于 E 点,$BE = 1,AE = 5,∠AEC = 30^{\circ}$,则 CD 的长为______.

答案：
$4\sqrt{2}$ 【解析】如图，过 O 作 OF⊥DC 于 F，连接 OC，则∠OFE = ∠OFC = 90°.
∵ BE = 1，AE = 5，
∴ AB = BE + AE = 6，
∴ OB = OA = OC = 3，
∴ OE = 3 - 1 = 2.
∵ ∠AEC = 30°，
∴ OF = $\frac{1}{2}$OE = 1，
∴ CF = $\sqrt{OC^2 - OF^2} = \sqrt{3^2 - 1^2} = 2\sqrt{2}$.
∵ OF⊥CD，OF 过圆心 O，
∴ DF = CF = $2\sqrt{2}$，
∴ CD = CF + DF = $4\sqrt{2}$，故答案为$4\sqrt{2}$.

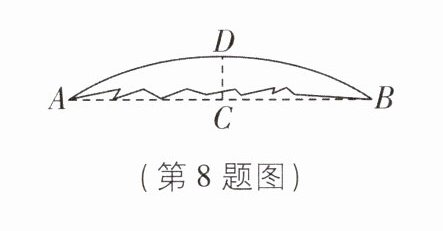
8 一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦 AB 长 20 厘米,弓形高 CD 为 2 厘米,则镜面半径为______厘米.

答案：
26 【解析】如图，设点 O 是玻璃镜面所在圆的圆心，连接 OC，OA.由题意可得 C 是 AB 的中点，CD⊥AB，
∴ OC⊥AB，AC = $\frac{1}{2}$AB = 10 厘米，
∴ O，C，D 三点共线.设镜面半径为 x 厘米.由题意可得$x^2 = 10^2 + (x - 2)^2$，
∴ x = 26，
∴ 镜面半径为 26 厘米.

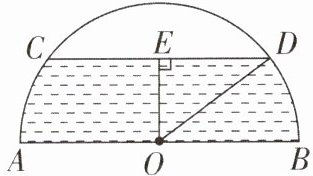
9 [2025 浙江杭州期中]如图是一个半圆形桥洞的截面示意图,圆心为 O,直径 AB 是河底线,弦 CD 是水位线,连接 OD,$CD// AB,AB = 10$米,$OE⊥CD$于点 E,$OE:CD = 3:8$.
(1)求 CD 的长;
(2)若水位以 0.4 米/时的速度上升,则经过多长时间桥洞会被灌满?

答案：
（1）
∵ AB = 10 米，
∴ OD = OB = $\frac{1}{2}$AB = 5 米.
∵ OE⊥CD，
∴ DE = $\frac{1}{2}$CD.
∵ OE∶CD = 3∶8，
∴ OE∶DE = 3∶4.设 OE = 3x 米，则 DE = 4x 米.在 Rt△ODE 中，由勾股定理得$(3x)^2 + (4x)^2 = 5^2$，解得 x = 1（负值已舍去），
∴ DE = 4 米，
∴ CD = 2DE = 8 米.
（2）由（1）得 OE = 3 米.如图，延长 OE 交半圆 O 于点 F，
∴ EF = OF - OE = 5 - 3 = 2（米），
∴ 2÷0.4 = 5（时）.

答：经过 5 小时桥洞被灌满.

10 $\odot O$的半径是 13,弦$AB// CD,AB = 24,CD = 10$,则 AB 与 CD 的距离是______.

答案：
17 或 7 【解析】作 OE⊥AB 于 E，OF⊥CD 于 F，则 AE = $\frac{1}{2}$AB = 12，CF = $\frac{1}{2}$CD = 5.连接 OA，OC，
∴ OA = OC = 13.
∵ AB//CD，
∴ E，O，F 三点共线.在 Rt△AOE 中，OE = $\sqrt{OA^2 - AE^2} = \sqrt{13^2 - 12^2} = 5$.在 Rt△OCF 中，OF = $\sqrt{OC^2 - CF^2} = \sqrt{13^2 - 5^2} = 12$.如图（1），当圆心 O 在弦 AB 与 CD 之间时，AB 与 CD 的距离为 OF + OE = 12 + 5 = 17；如图（2），当圆心 O 在弦 AB 与 CD 的外部时，AB 与 CD 的距离为 OF - OE = 12 - 5 = 7.综上，AB 与 CD 的距离是 17 或 7.