第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
8 [中]如图,点A,B的坐标分别是A(4,0),B(0,4),点C为坐标平面内一动点,BC= 2,点M为线段AC的中点,连接OM,则OM的最大值为(
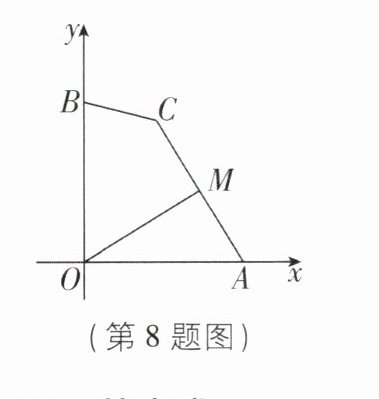
A.√2 + 1
B.√2 + 1 / 2
C.2√2 + 1
D.2√2 - 1 / 2
C
)
A.√2 + 1
B.√2 + 1 / 2
C.2√2 + 1
D.2√2 - 1 / 2
答案:
C
9 [2025山东烟台期中,较难]如图,在平面直角坐标系xOy中,半径为4的⊙O与x轴交于点A,B,与y轴交于点C,D,连接BC,已知x轴上一点P(8,0),点Q是⊙O上一动点,连接PQ,点M为PQ的中点,连接BM,CM,则△BCM面积的最小值为
$16 - 4\sqrt{2}$
.
答案:
$16 - 4\sqrt{2}$
如图,在Rt△ABC中,∠ABC= 90°,BC= 3,AC= 5,点D是其内部一动点,且∠DBC= ∠BAD,则C,D两点间的最小距离为(
A.3
B.4
C.√13 - 2
D.√13
C
)A.3
B.4
C.√13 - 2
D.√13
答案:
C
11 [2025河南开封期末,较难]如图,正方形ABCD的边长为4,点E,F分别是BC,CD上的动点,且BE= CF,连接AE,BF交于点P,连接CP,则CP的最小值是(
A.2√5 - 2
B.3√2 - 2
C.2√2
D.√2 + 2
A
)A.2√5 - 2
B.3√2 - 2
C.2√2
D.√2 + 2
答案:
A
12 [2024福建福州期中,中]如图,正方形ABCD的边长为6,点E是正方形外一动点,且点E在CD的右侧,∠AED= 45°,P为AB的中点,连接PE,当E运动时,线段PE的最大值为(
A.6√3
B.6√2
C.3 + 3√3
D.3 + 3√2
D
)A.6√3
B.6√2
C.3 + 3√3
D.3 + 3√2
答案:
D
13 [2025黑龙江绥化期末,较难]如图,已知菱形ABCD中,∠BAD= 120°,点E,F分别在AB,BC上,BE= CF,AF与CE交于点P,连接DP.
(1)求证:∠APE= 60°;
(2)当PC= 1,PA= 5时,求PD的长;
(3)当AB= 2√3时,求PD的最大值.
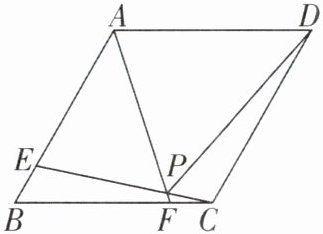

(1)求证:∠APE= 60°;
(2)当PC= 1,PA= 5时,求PD的长;
(3)当AB= 2√3时,求PD的最大值.


答案:
(1)[证明]如图
(1)所示,连接AC。
∵四边形ABCD是菱形,
∴AB=BC。
∵∠BAD=120°,
∴∠B=∠ADC=60°,
∴△ABC是等边三角形,
∴∠ACF=∠CBE=60°,AC=CB。又
∵CF=BE,
∴△ACF≌△CBE(SAS),
∴∠CAF=∠BCE,
∴∠APE=∠ACE + ∠CAF=∠BCE + ∠ACE=∠ACB=60°。
(2)[解]如图
(2),延长PC到M,使得CM=AP,连接DM。由
(1)易得∠AFC=∠CEB。
∵菱形ABCD中,AD//BC,AB//CD,
∴∠DAF + ∠AFC=180°,∠DCM=∠AEC,
∴∠CEB + ∠DAF=180°。
∵∠AEC + ∠CEB=180°,
∴∠DAF=∠AEC=∠DCM。又
∵AP=CM,AD=CD,
∴△ADP≌△CDM(SAS),
∴DP=DM,∠ADP=∠CDM,
∴∠ADC=∠PDM。
∵∠ADC=60°,
∴∠PDM=60°,
∴△PDM是等边三角形,
∴PD=PM=PC + CM=PC + PA=6。
(3)[解]
∵∠APE=60°,
∴∠APC=120°。
∵∠ADC=60°,
∴∠APC + ∠ADC=180°,
∴A,P,C,D四点共圆,
∴当PD为直径时,PD的值最大。设圆心为O,连接OA,OC,过点O作OM⊥AC于M,如图
(3)所示,
∴∠AOC=2∠ADC=120°。
∵OA=OC,
∴∠OAM=30°。
∵AC=AB=2√3,OM⊥AC,
∴AM=$\frac{1}{2}$AC=√3,
∴OM=$\frac{\sqrt{3}}{3}$AM=1,
∴OA=2,
∴PD的最大值为4。
(1)[证明]如图
(1)所示,连接AC。
∵四边形ABCD是菱形,
∴AB=BC。
∵∠BAD=120°,
∴∠B=∠ADC=60°,
∴△ABC是等边三角形,
∴∠ACF=∠CBE=60°,AC=CB。又
∵CF=BE,
∴△ACF≌△CBE(SAS),
∴∠CAF=∠BCE,
∴∠APE=∠ACE + ∠CAF=∠BCE + ∠ACE=∠ACB=60°。
(2)[解]如图
(2),延长PC到M,使得CM=AP,连接DM。由
(1)易得∠AFC=∠CEB。
∵菱形ABCD中,AD//BC,AB//CD,
∴∠DAF + ∠AFC=180°,∠DCM=∠AEC,
∴∠CEB + ∠DAF=180°。
∵∠AEC + ∠CEB=180°,
∴∠DAF=∠AEC=∠DCM。又
∵AP=CM,AD=CD,
∴△ADP≌△CDM(SAS),
∴DP=DM,∠ADP=∠CDM,
∴∠ADC=∠PDM。
∵∠ADC=60°,
∴∠PDM=60°,
∴△PDM是等边三角形,
∴PD=PM=PC + CM=PC + PA=6。
(3)[解]
∵∠APE=60°,
∴∠APC=120°。
∵∠ADC=60°,
∴∠APC + ∠ADC=180°,
∴A,P,C,D四点共圆,
∴当PD为直径时,PD的值最大。设圆心为O,连接OA,OC,过点O作OM⊥AC于M,如图
(3)所示,
∴∠AOC=2∠ADC=120°。
∵OA=OC,
∴∠OAM=30°。
∵AC=AB=2√3,OM⊥AC,
∴AM=$\frac{1}{2}$AC=√3,
∴OM=$\frac{\sqrt{3}}{3}$AM=1,
∴OA=2,
∴PD的最大值为4。
如图,已知点A,B的坐标分别是(0,1),(0,3),点C为x轴正半轴上一动点,当∠ACB最大时,点C的坐标是(
A.(2,0)
B.(√3,0)
C.(√2,0)
D.(1,0)
B
)A.(2,0)
B.(√3,0)
C.(√2,0)
D.(1,0)
答案:
【解析】:本题可根据圆的性质,通过确定∠ACB最大时点C的位置来求解其坐标。
设点C的坐标为$(x,0)(x\gt0)$,以线段AB为弦,所对圆周角为∠ACB,根据圆周角与圆心角的关系以及圆的性质,当圆与$x$轴相切时,∠ACB最大。
已知$A(0,1)$,$B(0,3)$,则线段$AB$的长度为$3 - 1 = 2$,设圆心为$M$,因为圆与$x$轴相切,所以圆心$M$的纵坐标等于圆的半径。
又因为$AB$为弦,且$AB$垂直于$x$轴,所以圆心$M$在线段$AB$的垂直平分线上,线段$AB$垂直平分线的方程为$y = 2$,即圆心$M$的纵坐标为$2$,那么圆的半径$r = 2$。
设圆心$M$的坐标为$(m,2)$,因为圆与$x$轴相切,所以圆心到$x$轴的距离等于半径,即$M$到$x$轴的距离为$2$。
连接$MA$,根据两点间距离公式$d=\sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$,可得$MA = r = 2$,已知$A(0,1)$,$M(m,2)$,则$\sqrt{(m - 0)^2+(2 - 1)^2}= 2$,即$\sqrt{m^2 + 1}= 2$,两边同时平方可得$m^2 + 1 = 4$,移项可得$m^2 = 3$,解得$m = \pm\sqrt{3}$。
因为点$C$在$x$轴正半轴,且圆与$x$轴相切于点$C$时∠ACB最大,此时圆心$M$在$x$轴右侧,所以$m = \sqrt{3}$,即圆心$M$的坐标为$(\sqrt{3},2)$,那么切点$C$的坐标为$(\sqrt{3},0)$。
【答案】:B。
设点C的坐标为$(x,0)(x\gt0)$,以线段AB为弦,所对圆周角为∠ACB,根据圆周角与圆心角的关系以及圆的性质,当圆与$x$轴相切时,∠ACB最大。
已知$A(0,1)$,$B(0,3)$,则线段$AB$的长度为$3 - 1 = 2$,设圆心为$M$,因为圆与$x$轴相切,所以圆心$M$的纵坐标等于圆的半径。
又因为$AB$为弦,且$AB$垂直于$x$轴,所以圆心$M$在线段$AB$的垂直平分线上,线段$AB$垂直平分线的方程为$y = 2$,即圆心$M$的纵坐标为$2$,那么圆的半径$r = 2$。
设圆心$M$的坐标为$(m,2)$,因为圆与$x$轴相切,所以圆心到$x$轴的距离等于半径,即$M$到$x$轴的距离为$2$。
连接$MA$,根据两点间距离公式$d=\sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$,可得$MA = r = 2$,已知$A(0,1)$,$M(m,2)$,则$\sqrt{(m - 0)^2+(2 - 1)^2}= 2$,即$\sqrt{m^2 + 1}= 2$,两边同时平方可得$m^2 + 1 = 4$,移项可得$m^2 = 3$,解得$m = \pm\sqrt{3}$。
因为点$C$在$x$轴正半轴,且圆与$x$轴相切于点$C$时∠ACB最大,此时圆心$M$在$x$轴右侧,所以$m = \sqrt{3}$,即圆心$M$的坐标为$(\sqrt{3},2)$,那么切点$C$的坐标为$(\sqrt{3},0)$。
【答案】:B。
查看更多完整答案,请扫码查看


