第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1 [2025 江苏徐州调研]下列说法:①面积相等的圆是等圆;②过圆心的线段是直径;③长度相等的弧是等弧;④半径是弦;⑤直径是最长的弦;⑥等弧所在的圆一定是等圆或同圆.其中正确的个数为(
A.1 个
B.2 个
C.3 个
D.4 个
C
)A.1 个
B.2 个
C.3 个
D.4 个
答案:
C 【解析】①面积相等的圆是等圆,故原说法正确;②连接圆上两点并通过圆心的线段是圆的直径,故原说法错误;③能够互相重合的弧叫做等弧,故原说法错误;④连接圆上任意两点的线段叫做弦,半径不是弦,故原说法错误;⑤直径是最长的弦,故原说法正确;⑥等弧所在的圆一定是等圆或同圆,故原说法正确.综上,正确的说法有①⑤⑥,共3个.故选C.
如图,点 A,B,C 均在$\odot O$上,D 为线段 AB 上一点,下列说法正确的是(
A.线段 AB,AC,CD 都是$\odot O$的弦
B.线段 AC 是$\odot O$的直径
C.AD= BD
D.弦 AB 把圆分成两条弧,其中$\overset{\frown }{ACB}$是劣弧
B
)A.线段 AB,AC,CD 都是$\odot O$的弦
B.线段 AC 是$\odot O$的直径
C.AD= BD
D.弦 AB 把圆分成两条弧,其中$\overset{\frown }{ACB}$是劣弧
答案:
B 【解析】A 线段AB,AC都是⊙O的弦,线段CD不是⊙O的弦,所以A选项不符合题意;B 线段AC是⊙O的直径,所以B选项符合题意;C 当点D为AB的中点时,AD=BD,所以C选项不符合题意;D $\overset{\frown }{ACB}$为优弧,所以D选项不符合题意.故选B.
3 如图,在扇形 AOB 中,D 为$\overset{\frown }{AB}$上的点,连接 AD 并延长与 OB 的延长线交于点 C. 若 CD= OA,$∠O= 75^{\circ }$,则$∠A$的度数为( )

A.$35^{\circ }$
B.$52.5^{\circ }$
C.$70^{\circ }$
D.$72^{\circ }$

A.$35^{\circ }$
B.$52.5^{\circ }$
C.$70^{\circ }$
D.$72^{\circ }$
答案:
C 【解析】连接OD,如图.设∠C的度数为n.
∵CD=OA=OD,
∴∠C=∠DOC=n,∠OAD=∠ADO.
∵∠ADO=∠DOC+∠C=2n,
∴∠OAD=2n.
∵∠AOC+∠C+∠OAD=180°,∠AOC=75°,
∴75°+n+2n=180°,解得n=35°,
∴∠OAD=2n=70°.故选C.

C 【解析】连接OD,如图.设∠C的度数为n.
∵CD=OA=OD,
∴∠C=∠DOC=n,∠OAD=∠ADO.
∵∠ADO=∠DOC+∠C=2n,
∴∠OAD=2n.
∵∠AOC+∠C+∠OAD=180°,∠AOC=75°,
∴75°+n+2n=180°,解得n=35°,
∴∠OAD=2n=70°.故选C.

4 如图,在$\odot O$中,AB 是弦,C 是弧 AB 上一点. 若$∠OAB= 25^{\circ },∠OCA= 40^{\circ }$,则$∠BOC$的度数为(
A.$30^{\circ }$
B.$40^{\circ }$
C.$50^{\circ }$
D.$60^{\circ }$
A
)A.$30^{\circ }$
B.$40^{\circ }$
C.$50^{\circ }$
D.$60^{\circ }$
答案:
A 【解析】
∵OA=OB,∠OAB=25°,
∴∠OBA=∠OAB=25°,
∴∠AOB=180°-∠OAB-∠OBA=130°.
∵OA=OC,∠OCA=40°,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°-∠OAC-∠OCA=100°,
∴∠BOC=∠AOB-∠AOC=130°-100°=30°,故选A.
∵OA=OB,∠OAB=25°,
∴∠OBA=∠OAB=25°,
∴∠AOB=180°-∠OAB-∠OBA=130°.
∵OA=OC,∠OCA=40°,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°-∠OAC-∠OCA=100°,
∴∠BOC=∠AOB-∠AOC=130°-100°=30°,故选A.
5 [2024 江苏盐城调研]如图,OA 是$\odot O$的半径,B 为 OA 上一点(且不与点 O,A 重合),过点 B 作 OA 的垂线交$\odot O$于点 C. 以 OB,BC 为边作矩形 OBCD,连接 BD. 若 CD= 6,BC= 8,则 AB 的长为______.


答案:
4 【解析】如图,连接OC.
∵四边形OBCD是矩形,
∴∠OBC=90°,OB=CD=6,
∴OA=OC=$\sqrt{B{C}^{2}+O{B}^{2}}$=10,
∴AB=OA-OB=4,故答案为4.

4 【解析】如图,连接OC.
∵四边形OBCD是矩形,
∴∠OBC=90°,OB=CD=6,
∴OA=OC=$\sqrt{B{C}^{2}+O{B}^{2}}$=10,
∴AB=OA-OB=4,故答案为4.

6 [2025 江苏无锡质检]如图,圆 O 的周长为 4π,B 是弦 CD 上任意一点(与 C,D 不重合),过 B 作 OC 的平行线交 OD 于点 E,则 EO+EB 的值为______
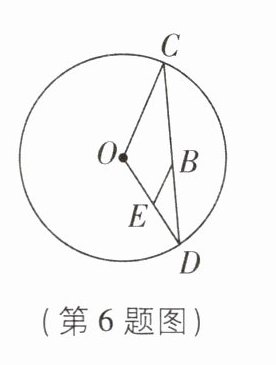
2
.
答案:
2 【解析】
∵圆O的周长为4π,
∴OD=2.
∵OC=OD,
∴∠C=∠D.
∵BE//OC,
∴∠EBD=∠C,
∴∠EBD=∠D,
∴BE=DE,
∴EO+EB=OD=2.故答案为2.
∵圆O的周长为4π,
∴OD=2.
∵OC=OD,
∴∠C=∠D.
∵BE//OC,
∴∠EBD=∠C,
∴∠EBD=∠D,
∴BE=DE,
∴EO+EB=OD=2.故答案为2.
7 如图,在半圆 O 中,AB 是直径,CD 是一条弦,若 AB= 10,则$\triangle COD$面积的最大值是______.
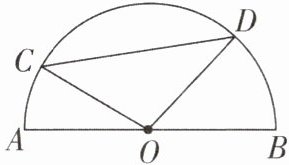

答案:
12.5 【解析】如图,作DH⊥CO交CO的延长线于H.
∵${S}_{\triangle COD}=\frac{1}{2}\cdot OC\cdot DH$,且DH≤OD,
∴当DH=OD时,△COD的面积最大,此时△COD是等腰直角三角形,∠COD=90°.又
∵OC=OD=$\frac{1}{2}AB$=5,
∴△COD的面积的最大值为$\frac{1}{2}× 5× 5$=12.5.故答案为12.5.

12.5 【解析】如图,作DH⊥CO交CO的延长线于H.
∵${S}_{\triangle COD}=\frac{1}{2}\cdot OC\cdot DH$,且DH≤OD,
∴当DH=OD时,△COD的面积最大,此时△COD是等腰直角三角形,∠COD=90°.又
∵OC=OD=$\frac{1}{2}AB$=5,
∴△COD的面积的最大值为$\frac{1}{2}× 5× 5$=12.5.故答案为12.5.

8 [2025 江苏宿迁期中]如图,在$\triangle ABC$中,AB= AC,点 D,E 在边 BC 上,BD= CE. 过 A,D,E 三点作$\odot O$,连接 AO 并延长,交 BC 于点 F.
(1)求证:AF⊥BC;
(2)若 AB= 10,BC= 12,BD= 2,求$\odot O$的半径长.
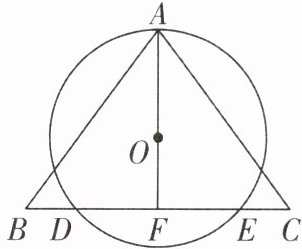
(1)求证:AF⊥BC;
(2)若 AB= 10,BC= 12,BD= 2,求$\odot O$的半径长.

答案:
(1)【证明】如图,连接AD,AE.
∵AB=AC,
∴∠B=∠C.在△ABD与△ACE中,$\left\{\begin{array}{l}AB=AC,\\ \angle B=\angle C,\\ BD=CE,\end{array}\right.$
∴△ABD≌△ACE(SAS),
∴AD=AE.连接OD,OE,则OD=OE.
∵AO=AO,
∴△ADO≌△AEO(SSS),
∴∠DAF=∠EAF,
∴AF⊥BC.
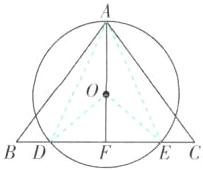
关键点拨 利用矩形的对角线相等即可得到所求结果.
关键点拨 作DH⊥CO交CO的延长线于H.解题关键是证明当DH=OD时,△COD的面积最大,此时△COD是等腰直角三角形.
思路分析 作辅助线OF⊥AB,利用折叠的性质得出OF=$\frac{1}{2}AO$,再根据直角三角形的性质及平行线的性质得出∠AOC=30°,最后利用弧的度数与圆心角度数的关系得出结论.
(2)【解】
∵AB=AC,AF⊥BC,BC=12,
∴BF=CF=$\frac{1}{2}BC$=6,
∴AF=$\sqrt{A{B}^{2}-B{F}^{2}}=\sqrt{{10}^{2}-{6}^{2}}$=8.
∵BD=2,
∴DF=4.设DO=AO=x,
∴OF=AF-OA=8-x.在Rt△ODF中,O${D}^{2}=O{F}^{2}+D{F}^{2}$,
∴${x}^{2}={(8-x)}^{2}+{4}^{2}$,
∴x=5,即⊙O的半径长为5.
(1)【证明】如图,连接AD,AE.
∵AB=AC,
∴∠B=∠C.在△ABD与△ACE中,$\left\{\begin{array}{l}AB=AC,\\ \angle B=\angle C,\\ BD=CE,\end{array}\right.$
∴△ABD≌△ACE(SAS),
∴AD=AE.连接OD,OE,则OD=OE.
∵AO=AO,
∴△ADO≌△AEO(SSS),
∴∠DAF=∠EAF,
∴AF⊥BC.

关键点拨 利用矩形的对角线相等即可得到所求结果.
关键点拨 作DH⊥CO交CO的延长线于H.解题关键是证明当DH=OD时,△COD的面积最大,此时△COD是等腰直角三角形.
思路分析 作辅助线OF⊥AB,利用折叠的性质得出OF=$\frac{1}{2}AO$,再根据直角三角形的性质及平行线的性质得出∠AOC=30°,最后利用弧的度数与圆心角度数的关系得出结论.
(2)【解】
∵AB=AC,AF⊥BC,BC=12,
∴BF=CF=$\frac{1}{2}BC$=6,
∴AF=$\sqrt{A{B}^{2}-B{F}^{2}}=\sqrt{{10}^{2}-{6}^{2}}$=8.
∵BD=2,
∴DF=4.设DO=AO=x,
∴OF=AF-OA=8-x.在Rt△ODF中,O${D}^{2}=O{F}^{2}+D{F}^{2}$,
∴${x}^{2}={(8-x)}^{2}+{4}^{2}$,
∴x=5,即⊙O的半径长为5.
查看更多完整答案,请扫码查看


