《2025年初中必刷题九年级数学上册苏科版》

1 [2025 江苏无锡质检]如图,在宽为 20m、长为 32m 的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪。要使草坪的面积为$ 540m^2,$求道路的宽。如果设道路宽为 xm,根据题意,所列方程正确的是 (A)


A.(20 - x)(32 - x) = 540
B.(20 - x)(32 - x) = 32×20 - 540
C.(20 - 2x)(32 - 2x) = 540
D.(20 - 2x)(32 - 2x) = 32×20 - 540

答案： A 【解析】根据题意得$(20 - x)(32 - x)=540.$故选 A.

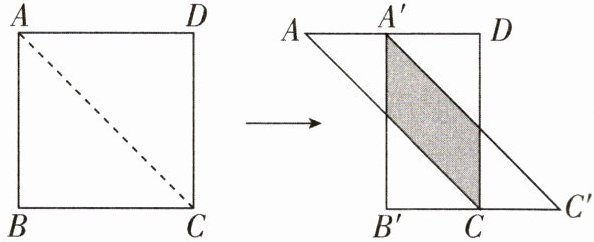
2 [2025 江苏徐州调研]如图,将边长为 15 的正方形 ABCD 沿其对角线 AC 剪开,再把△ABC 沿着 AD 方向平移,得到△A'B'C',当两个三角形重叠部分的面积为 56 时,它移动的距离 AA'等于 。

答案：
7 或 8 【解析】如图,设$AA' = x$,$AC$与$A'B'$相交于点 G.
∵ △ACD 是将 正方形 ABCD 剪开得到的,$\therefore △ACD$是等腰直角三角形,$\therefore ∠A = 45^{\circ },$
∴ 易得$△AA'G$是等腰直角三角形,$\therefore A'G = AA' = x$,$A'D = AD - AA' = 15 - x$.
∵ 两个三角形重叠部分的面积为 56,易知重叠部分是平行四边形,$\therefore x(15 - x)=56$,解得$x_{1}=7$,$x_{2}=8$,即移动的距离$AA'$为 7 或 8.故答案为 7 或 8.

3 新素材 [2025 湖北武汉调研]长江文化艺术季于 2024 年 9 月在武汉开幕,主办方须在空地上布置烟花,如图,已知空地上有一段长为 15 米的旧墙 MN,若利用该旧墙和防火护栏围成一个矩形燃放地 ABCD,其中 AD ≤ MN,已知该矩形燃放地的一边靠墙,另外三边一共用了 24 米的防火护栏,设 AB = x 米,矩形 ABCD 的面积为 S 平方米。
(1)BC = (24 - 2x)米,S = x(24 - 2x)平方米；(用含 x 的代数式表示)
(2)所围成的矩形燃放地面积能否为 90 平方米？若能,请求出 AD 的长,若不能,请说明理由。

【解】(2)不能,理由:令$(24 - 2x)x = 90$,整理得$x^{2}-12x + 45 = 0.\because b^{2}-4ac = (-12)^{2}-4×45 ＜ 0$,∴ 此方程无实数根,∴ 所围成的矩形燃放地面面积不能为 90 平方米.

答案： 【解】
(1)由题意得$CD = AB = x$米,$\therefore BC = (24 - 2x)$米,$S = AB×BC = x(24 - 2x)$平方米.故答案为$(24 - 2x)$,$x(24 - 2x).$
(2)不能,理由:令$(24 - 2x)x = 90$,整理得$x^{2}-12x + 45 = 0.\because b^{2}-4ac = (-12)^{2}-4×45 ＜ 0$,
∴ 此方程无实数根,
∴ 所围成的矩形燃放地面面积不能为 90 平方米.

4 新素材 [2025 上海闵行区期中]2024 年世界互联网大会·乌镇峰会于 11 月 19 日至 22 日在浙江乌镇举行。本次峰会将全面聚焦人工智能。某高校开设了人工智能相关选修课程(一年修满学分),已知 2022 年和 2024 年报名的学生分别为 100 人和 169 人,2022~2024 年每年的报名人数平均增长率相同,那么年平均增长率是30%。

答案： 30% 【解析】设年平均增长率是 x. 根据题意得,$100(1 + x)^{2}=169$,解得$x_{1}=-2.3$(不合题意,舍去),$x_{2}=0.3 = 30\% $,故答案为 30%.

(1)若设乙店八、九月份销售额的月平均增长率为 x,则甲店九月份的销售额为6(1 + 2x)²万元,乙店九月份的销售额为9(1 + x)²万元。(用含 x 的代数式表示)
(2)甲店、乙店八、九这两个月份销售额的月平均增长率各是多少？
【解】(2)由题意得,$6(1 + 2x)^{2}-9(1 + x)^{2}=6$,解得$x_{1}=0.6 = 60\% $,$x_{2}=-1$(舍去),$\therefore 2x = 120\% $.答:甲店、乙店八、九这两个月份销售额的月平均增长率分别是 120%,60%.

答案： 【解】
(1)
∵ 乙店八、九月份销售额的月平均增长率为 x,
∴ 甲店九月份的销售额为$6(1 + 2x)^{2}$万元,乙店九月份的销售额为$9(1 + x)^{2}$万元.故答案为$6(1 + 2x)^{2}$,$9(1 + x)^{2}.$
(2)由题意得,$6(1 + 2x)^{2}-9(1 + x)^{2}=6$,解得$x_{1}=0.6 = 60\% $,$x_{2}=-1$(舍去),$\therefore 2x = 120\% $.答:甲店、乙店八、九这两个月份销售额的月平均增长率分别是 120%,60%.