《2025年初中必刷题九年级数学上册苏科版》

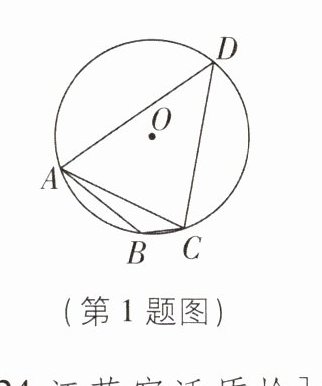
1[2024江苏无锡质检]如图,四边形ABCD内接于$\odot O,∠ABC= 135^{\circ },AC= 1$,则$\odot O$的半径为( )


A.1
B.$\sqrt {2}$
C.$\frac {\sqrt {2}}{2}$
D.$\frac {\sqrt {3}}{3}$

答案：
C 【解析】连接 OA,OC,如图:
∵ 四边形 ABCD 内接于$\odot O$，$∠ABC = 135^{\circ}$，$\therefore ∠ADC = 45^{\circ}$，$\therefore ∠AOC = 90^{\circ}$。在$Rt△AOC$中，由勾股定理得$OA^{2}+OC^{2}=AC^{2}$。$\because OA = OC$，$AC = 1$，$\therefore OA = \frac{\sqrt{2}}{2}$，$\therefore \odot O$的半径为$\frac{\sqrt{2}}{2}$。故选 C。

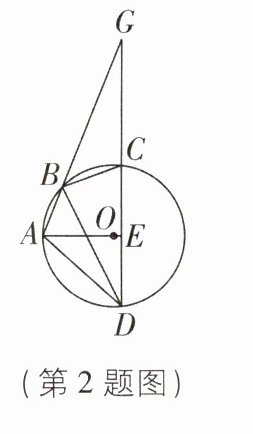
2[2024江苏宿迁质检]如图,四边形ABCD为$\odot O$的内接四边形.弦AB所在直线与DC的延长线相交于点G,$AO⊥CD$,垂足为E,连接BD,$∠GBC= 48^{\circ }$,则$∠DBC$的度数为( )


A.$84^{\circ }$
B.$72^{\circ }$
C.$66^{\circ }$
D.$48^{\circ }$

答案：
A 【解析】如图，连接 AC。
∵ 四边形 ABCD 为$\odot O$的内接四边形，
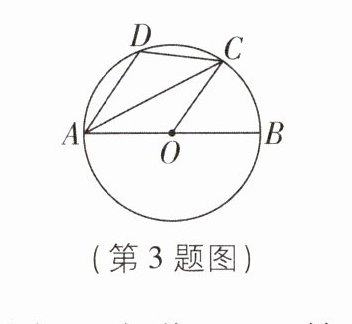
∴ 易得$∠ADC = ∠GBC = 48^{\circ}$。$\because AO⊥CD$，$\therefore DE = CE$，$∠AED = 90^{\circ}$，$\therefore ∠DAE = 180^{\circ}-∠ADC - ∠AED = 42^{\circ}$，$\therefore ∠CAD = 2∠DAE = 84^{\circ}$。由圆周角定理得$∠DBC = ∠CAD = 84^{\circ}$，故选 A。D33$\therefore ∠CAD = 2∠DAE = 84^{\circ}$。由圆周角定理得$∠DBC = ∠CAD = 84^{\circ}$，故选 A。

3[2025江苏南京期中]如图,AB为$\odot O$的直径,C为$\widehat {AB}$上一点,$AD// OC$,AD交$\odot O$于点D,连接AC,CD,设$∠BOC= x^{\circ },∠ACD= y^{\circ }$,则下列结论成立的是( )


A.$x+y= 90$
B.$2x+y= 90$
C.$2x+y= 180$
D.$x= y$

答案：
A 【解析】连接 BC，如图。
∵ AB 是$\odot O$的直径，$\therefore ∠ACB = 90^{\circ}$。
∵ 四边形 ADCB 是圆的内接四边形，$\therefore ∠ACB + ∠ACD + ∠BAD = 180^{\circ}$。$\because AD// OC$，$\therefore ∠BAD = ∠BOC = x^{\circ}$。$\because ∠ACD = y^{\circ}$，$\therefore x + y + 90 = 180$，$\therefore x + y = 90$。

4如图,四边形ABCD是$\odot O$的内接四边形,BE是$\odot O$的直径,连接BD.若$∠BCD= 2∠BAD$,则$∠EBD$的度数是( )


A.$30^{\circ }$
B.$35^{\circ }$
C.$45^{\circ }$
D.$60^{\circ }$

答案：
A 【解析】连接 DE，如图。
∵ 四边形 ABCD 是$\odot O$的内接四边形，$\therefore ∠BAD + ∠BCD = 180^{\circ}$。$\because ∠BCD = 2∠BAD$，$\therefore ∠BAD = 60^{\circ}$。
∵ BE 是$\odot O$的直径，$\therefore ∠BDE = 90^{\circ}$。$\because ∠BED = ∠BAD = 60^{\circ}$，
∴ 在$Rt△BED$中，$∠EBD = 90^{\circ}-60^{\circ}= 30^{\circ}$。故选 A。

5[2023江苏淮安中考]如图,四边形ABCD是$\odot O$的内接四边形,BC是$\odot O$的直径,$BC= 2CD$,则$∠BAD$的度数是______°.

答案：
120 【解析】如图，连接 OD。
∵ BC 是$\odot O$的直径，$BC = 2CD$，$\therefore OC = OD = CD$，$\therefore △COD$为等边三角形，$\therefore ∠C = 60^{\circ}$。
∵ 四边形 ABCD 是$\odot O$的内接四边形，$\therefore ∠BAD + ∠C = 180^{\circ}$，$\therefore ∠BAD = 120^{\circ}$，故答案为 120。

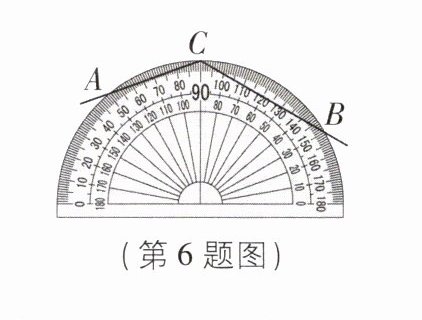
6[2025浙江宁波期中]在利用量角器测量$∠ACB$的度数时,小文同学放错了位置,将角的顶点放到了量角器的弧线上(如图),爱思考的李涛同学忽然发现,这样测量也能得到$∠ACB$的度数.通过仔细观察,李涛同学发现射线CA,CB与量角器的交点A和B对应的刻度分别是$50^{\circ }和150^{\circ }$,则$∠ACB$的度数为______.

答案：
130°【解析】根据题意构造$\odot O$，在下半圆上取点 D，连接 OA，OB，DA，DB，设$\odot O$的直径为 EF，如图。由题意可知，$∠AOE = 50^{\circ}$，$∠EOB = 150^{\circ}$，$\therefore ∠AOB = ∠EOB - ∠AOE = 150^{\circ}-50^{\circ}= 100^{\circ}$，$\therefore ∠ADB = \frac{1}{2}∠AOB = 50^{\circ}$。
∵ 点 A，B，C，D 均在$\odot O$上，$\therefore ∠ACB + ∠ADB = 180^{\circ}$，$\therefore ∠ACB = 130^{\circ}$。故答案为$130^{\circ}$。

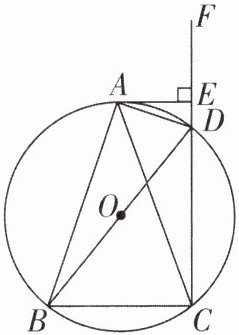
7如图,四边形ABCD是$\odot O$的内接四边形,点F是CD延长线上的一点,且DA平分$∠BDF,AE⊥CD$交CD延长线于点E.
(1)求证:$AB= AC$.
(2)若$BD= 11,DE= 2$,求CD的长.

答案：

(1)【证明】
∵ DA 平分$∠BDF$，$\therefore ∠ADF = ∠ADB$。$\because ∠ABC + ∠ADC = 180^{\circ}$，$∠ADC + ∠ADF = 180^{\circ}$，$\therefore ∠ABC = ∠ADF$。$\because ∠ACB = ∠ADB$，$\therefore ∠ABC = ∠ACB$，$\therefore AB = AC$。
(2)【解】如图，过点 A 作$AG⊥BD$，垂足为 G。
∵ DA 平分$∠BDF$，$AE⊥CF$，$AG⊥BD$，$\therefore AG = AE$，$∠AGD = ∠AGB = ∠AEC = 90^{\circ}$。在$Rt△AED$和$Rt△AGD$中，$AE = AG$，$AD = AD$，$\therefore Rt△AED\cong Rt△AGD(HL)$，$\therefore ED = GD = 2$。在$Rt△AEC$和$Rt△AGB$中，$AE = AG$，$AC = AB$，$\therefore Rt△AEC\cong Rt△AGB(HL)$，$\therefore CE = BG$。$\because BD = 11$，$\therefore BG = BD - GD = 11 - 2 = 9$，$\therefore CE = BG = 9$，$\therefore CD = CE - DE = 9 - 2 = 7$。

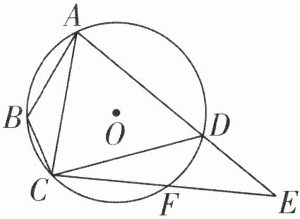
8如图,四边形ABCD内接于$\odot O$,F是$\widehat {CD}$上一点,且$\widehat {DF}= \widehat {BC}$,连接CF并延长交AD的延长线于点E,连接AC.
(1)若$∠B= 125^{\circ },∠BAC= 25^{\circ }$,求$∠E$的度数;
(2)若$\odot O$的半径为6,且$∠B= 2∠ADC$,求AC的长.

答案：

(1)【解】
∵ 四边形 ABCD 内接于$\odot O$，$∠ABC = 125^{\circ}$，$\therefore ∠ADC = 180^{\circ}-∠ABC = 55^{\circ}$。$\because \widehat{DF}=\widehat{BC}$，$∠BAC = 25^{\circ}$，$\therefore ∠DCE = ∠BAC = 25^{\circ}$，$\therefore ∠E = ∠ADC - ∠DCE = 55^{\circ}-25^{\circ}= 30^{\circ}$。
(2)如图，连接 AO，CO，过 O 作$OH⊥AC$于点 H，则$AO = CO = 6$。
∵ 四边形 ABCD 内接于$\odot O$，$\therefore ∠B + ∠ADC = 180^{\circ}$。$\because ∠B = 2∠ADC$，$\therefore ∠ADC = 60^{\circ}$，$\therefore ∠AOC = 2∠ADC = 120^{\circ}$。$\because OA = OC$，$\therefore ∠OAC = ∠OCA = \frac{1}{2}(180^{\circ}-∠AOC)= 30^{\circ}$。$\because AO = 6$，$OH⊥AC$，$\therefore OH = \frac{1}{2}AO = 3$，由勾股定理得$AH = \sqrt{AO^{2}-OH^{2}}=\sqrt{6^{2}-3^{2}}= 3\sqrt{3}$。$\because OH⊥AC$，OH 过圆心 O，$\therefore AH = CH = 3\sqrt{3}$，$\therefore AC = AH + CH = 6\sqrt{3}$。