《2025年初中必刷题九年级数学上册苏科版》

1 [中]小刚在解关于 $ x $ 的方程 $ a x ^ { 2 } + b x + c = 0 ( a \neq 0 ) $ 时,只抄对了 $ a = 1 $,$ b = 4 $,解出其中一个根是 $ x = - 1 $。他核对时发现所抄的 $ c $ 比原方程的 $ c $ 值小 $ 2 $,则原方程的根的情况是(A)
A.不存在实数根
B.有两个不相等的实数根
C.有一个根是 $ x = - 1 $
D.有两个相等的实数根

答案： A 【解析】根据题意可知,原方程为$x^{2}+4x+c=0$,且$x=-1$是方程$x^{2}+4x+c-2=0$的一个根,$\therefore 1-4+c-2=0$,解得$c=5$,则原方程为$x^{2}+4x+5=0$.$\because 4^{2}-4×1×5=-4＜0$,$\therefore$原方程不存在实数根.故选 A.

已知方程 $ x ^ { 2 } - 2 | x | - 15 = 0 $,则此方程的所有实数根的和为(A)
A.$ 0 $
B.$ - 2 $
C.$ 2 $
D.$ 8 $

答案： A 【解析】①当$x＞0$时,方程化为$x^{2}-2x-15=0$,即$(x+3)(x-5)=0$,$\therefore x+3=0$或$x-5=0$,解得$x_{1}=-3$(舍去),$x_{2}=5$;②当$x＜0$时,方程化为$x^{2}+2x-15=0$,即$(x-3)(x+5)=0$,$\therefore x-3=0$或$x+5=0$,解得$x_{3}=3$(舍去),$x_{4}=-5$;③当$x=0$时,方程不成立.$\therefore$此方程的所有实数根的和为$5+(-5)=0$.故选 A.

若关于 $ x $ 的方程 $ a x ^ { 2 } + b x + c = 0 ( a \neq 0 ) $ 的两根之和是 $ m $,两根之积是 $ n $,则关于 $ t $ 的方程 $ a ( t + 1 ) ^ { 2 } + b ( t + 1 ) + c = 0 $ 的两根之积是(C)
A.$ n + m - 1 $
B.$ n + m + 1 $
C.$ n - m + 1 $
D.$ n - m - 1 $

答案： C 【解析】把方程$a(t+1)^{2}+b(t+1)+c=0$看作关于$t+1$的一元二次方程.设关于$x$的方程$ax^{2}+bx+c=0(a≠0)$的两根为$x_{1},x_{2}$,则方程$a(t+1)^{2}+b(t+1)+c=0$的两根为$t_{1}=x_{1}-1$,$t_{2}=x_{2}-1$.$\because$关于$x$的方程$ax^{2}+bx+c=0(a≠0)$的两根之和是$m$,两根之积是$n$,$\therefore x_{1}+x_{2}=m$,$x_{1}x_{2}=n$,$\therefore t_{1}t_{2}=(x_{1}-1)(x_{2}-1)=x_{1}x_{2}-(x_{1}+x_{2})+1=n-m+1$.故选 C.

关于 $ x $ 的一元二次方程 $ a x ^ { 2 } - 2 a x + b + 1 = 0 ( a b \neq 0 ) $ 有两个相等的实数根 $ k $,则下列选项成立的是(B)
A.若 $ - 1 ＜ a ＜ 0 $,则 $ \frac { k } { a } ＞ \frac { k } { b } $
B.若 $ \frac { k } { a } ＞ \frac { k } { b } $,则 $ 0 ＜ a ＜ 1 $
C.若 $ 0 ＜ a ＜ 1 $,则 $ \frac { k } { a } ＜ \frac { k } { b } $
D.若 $ \frac { k } { a } ＜ \frac { k } { b } $,则 $ - 1 ＜ a ＜ 0 $

答案： B 【解析】$\because$关于$x$的一元二次方程$ax^{2}-2ax+b+1=0(ab≠0)$有两个相等的实数根$k$,$\therefore (-2a)^{2}-4a(b+1)=0$,$4a^{2}-4ab-4a=0$.又$\because ab≠0$,$\therefore a-b-1=0$,即$a=b+1$,$\therefore ax^{2}-2ax+a=0$,解得$x_{1}=x_{2}=1$,$\therefore k=1$,$\therefore \frac {k}{a}-\frac {k}{b}=\frac {1}{a}-\frac {1}{a-1}=-\frac {1}{a(a-1)}$.当$\frac {k}{a}＞\frac {k}{b}$,即$\frac {k}{a}-\frac {k}{b}＞0$,$-\frac {1}{a(a-1)}＞0$时,$a(a-1)＜0$,即$\left\{\begin{array}{l} a＜0,\\ a-1＞0\end{array}\right. $或$\left\{\begin{array}{l} a＞0,\\ a-1＜0,\end{array}\right. $解得$0＜a＜1$;当$\frac {k}{a}＜\frac {k}{b}$,即$\frac {k}{a}-\frac {k}{b}＜0$,$-\frac {1}{a(a-1)}＜0$时,$a(a-1)＞0$,即$\left\{\begin{array}{l} a＞0,\\ a-1＞0\end{array}\right. $或$\left\{\begin{array}{l} a＜0,\\ a-1＜0,\end{array}\right. $解得$a＞1$或$a＜0$.故选 B.

5 [2025 江苏盐城调研,中]小华设计了一个魔术盒,将任意实数对 $ ( a, b ) $ 放入其中,会得到一个新的实数 $ a ^ { 2 } - 2 b - 3 $。若将实数对 $ ( 2 x, - x ) $ 放入其中得到实数 $ - 1 $,则 $ x $ 的值为-1 或$\frac {1}{2}$。

答案： -1 或$\frac {1}{2}$ 【解析】根据题意,得$(2x)^{2}-2(-x)-3=-1$,整理,得$2x^{2}+x-1=0$,即$(x+1)(2x-1)=0$,解得$x_{1}=-1$,$x_{2}=\frac {1}{2}$,故答案为-1 或$\frac {1}{2}$.

方程 $ ( x ^ { 2 } + 3 x - 4 ) ^ { 2 } + ( 2 x ^ { 2 } - 7 x + 6 ) ^ { 2 } = ( 3 x ^ { 2 } - 4 x + 2 ) ^ { 2 } $ 的负整数解为$x=-4$。

答案： $x=-4$ 【解析】设$x^{2}+3x-4=a$,$2x^{2}-7x+6=b$,则$3x^{2}-4x+2=a+b$,可得$a^{2}+b^{2}=(a+b)^{2}$,解得$ab=0$,$\therefore x^{2}+3x-4=0$或$2x^{2}-7x+6=0$,解得$x_{1}=-4$,$x_{2}=1$,$x_{3}=\frac {3}{2}$,$x_{4}=2$,$\therefore$方程$(x^{2}+3x-4)^{2}+(2x^{2}-7x+6)^{2}=(3x^{2}-4x+2)^{2}$的负整数解为$x=-4$,故答案为$x=-4$.

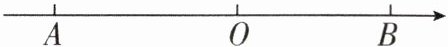
7 [2024 辽宁鞍山期中,中]如图,点 $ A $ 在数轴的负半轴,点 $ B $ 在数轴的正半轴,且点 $ A $ 对应的数是 $ 2 x - 1 $,点 $ B $ 对应的数是 $ x ^ { 2 } + x $,已知 $ A B = 5 $,则 $ x $ 的值为$\frac {1-\sqrt {17}}{2}$。

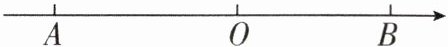
答案： $\frac {1-\sqrt {17}}{2}$ 【解析】根据题意,得$x^{2}+x-(2x-1)=5$,整理,得$x^{2}-x-4=0$.$\because a=1$,$b=-1$,$c=-4$,$\therefore (-1)^{2}-4×1×(-4)=17＞0$,则$x=\frac {-b\pm \sqrt {b^{2}-4ac}}{2a}=\frac {1\pm \sqrt {17}}{2}$,$\therefore x_{1}=\frac {1+\sqrt {17}}{2}$,$x_{2}=\frac {1-\sqrt {17}}{2}$.$\because$点 A 在数轴的负半轴,$\therefore 2x-1＜0$,即$x＜\frac {1}{2}$,$\therefore x=\frac {1-\sqrt {17}}{2}$,故答案为$\frac {1-\sqrt {17}}{2}$.

8 [中]已知 $ \triangle A B C $ 的两边 $ A B $,$ A C $ 的长是关于 $ x $ 的一元二次方程 $ x ^ { 2 } - 2 ( n - 1 ) x + n ^ { 2 } - 2 n = 0 $ 的两个根,第三边 $ B C $ 的长是 $ 10 $。问当 $ n $ 为何值时,$ \triangle A B C $ 为等腰三角形？并求 $ \triangle A B C $ 的周长。

答案： 【解】$\because b^{2}-4ac=[-2(n-1)]^{2}-4(n^{2}-2n)=4＞0$,$\therefore$无论$x$取何值,此方程总有两个不相等的实数根.$\because$第三边 BC 的长是 10,$\therefore$当$\triangle ABC$为等腰三角形时,$x=10$为一元二次方程的一个根,$\therefore 100-20(n-1)+n^{2}-2n=0$,解得$n=12$或10.
①当$n=12$时,方程变为$x^{2}-22x+120=0$.设等腰三角形的底边长为$m$.根据根与系数的关系,知$m+10=22$,$\therefore m=12$,$\therefore \triangle ABC$的周长为$10+10+12=32$;
②当$n=10$时,方程变为$x^{2}-18x+80=0$.设等腰三角形的底边长为$e$.根据根与系数的关系,知$10+e=18$,解得$e=8$,$\therefore \triangle ABC$的周长为$10+10+8=28$.
综上,当$n=12$时,$\triangle ABC$是等腰三角形,此时$\triangle ABC$的周长为32;当$n=10$时,$\triangle ABC$是等腰三角形,此时$\triangle ABC$的周长为28.

(1) 问题：方程 $ x ^ { 3 } + x ^ { 2 } - 2 x = 0 $ 的解是 $ x _ { 1 } = 0 $,$ x _ { 2 } = $-2,$ x _ { 3 } = $1；
(2) 拓展：利用“转化”思想求方程 $ \sqrt { 2 x + 3 } = x $ 的解；
【解】$\sqrt {2x+3}=x$,方程的两边平方,得$2x+3=x^{2}$,即$x^{2}-2x-3=0$,$(x-3)(x+1)=0$,$\therefore x-3=0$或$x+1=0$,$\therefore x_{1}=3$,$x_{2}=-1$.当$x=-1$时,$\sqrt {2x+3}=\sqrt {1}=1≠-1$,$\therefore x=-1$不是原方程的解,$\therefore$方程$\sqrt {2x+3}=x$的解是$x=3$
(3) 应用：如图,已知矩形草坪 $ A B C D $ 的长 $ A D = 8 \mathrm { m } $,宽 $ A B = 3 \mathrm { m } $。小华把一根长为 $ 10 \mathrm { m } $ 的绳子的一端固定在点 $ B $,沿草坪边沿 $ B A $,$ A D $ 走到点 $ P $ 处,把长绳 $ P B $ 段拉直并固定在点 $ P $,然后沿草坪边沿 $ P D $,$ D C $ 走到点 $ C $ 处,把长绳剩下的一段拉直,长绳的另一端恰好落在点 $ C $。求 $ A P $ 的长。
【解】$\because$四边形 ABCD 是矩形,$\therefore ∠A=∠D=90^{\circ }$,$AB=CD=3m$.设$AP=xm$,则$PD=(8-x)m$.$\because BP+CP=10$,$BP=\sqrt {AP^{2}+AB^{2}}$,$CP=\sqrt {CD^{2}+PD^{2}}$,$\therefore \sqrt {x^{2}+9}+\sqrt {(8-x)^{2}+9}=10$,$\therefore \sqrt {(8-x)^{2}+9}=10-\sqrt {x^{2}+9}$.两边平方,得$(8-x)^{2}+9=100-20\sqrt {x^{2}+9}+9+x^{2}$.整理,得$5\sqrt {x^{2}+9}=4x+9$.两边平方并整理,得$x^{2}-8x+16=0$,即$(x-4)^{2}=0$.$\therefore x=4$.经检验,$x=4$是原方程的解.
答:AP 的长为4m.

答案：
(1)$x_{1}=0$,$x_{2}=-2$,$x_{3}=1$；
(2)【解】$\sqrt {2x+3}=x$,方程的两边平方,得$2x+3=x^{2}$,即$x^{2}-2x-3=0$,$(x-3)(x+1)=0$,$\therefore x-3=0$或$x+1=0$,$\therefore x_{1}=3$,$x_{2}=-1$.当$x=-1$时,$\sqrt {2x+3}=\sqrt {1}=1≠-1$,$\therefore x=-1$不是原方程的解,$\therefore$方程$\sqrt {2x+3}=x$的解是$x=3$；
(3)【解】$\because$四边形 ABCD 是矩形,$\therefore ∠A=∠D=90^{\circ }$,$AB=CD=3m$.设$AP=xm$,则$PD=(8-x)m$.$\because BP+CP=10$,$BP=\sqrt {AP^{2}+AB^{2}}$,$CP=\sqrt {CD^{2}+PD^{2}}$,$\therefore \sqrt {x^{2}+9}+\sqrt {(8-x)^{2}+9}=10$,$\therefore \sqrt {(8-x)^{2}+9}=10-\sqrt {x^{2}+9}$.两边平方,得$(8-x)^{2}+9=100-20\sqrt {x^{2}+9}+9+x^{2}$.整理,得$5\sqrt {x^{2}+9}=4x+9$.两边平方并整理,得$x^{2}-8x+16=0$,即$(x-4)^{2}=0$.$\therefore x=4$.经检验,$x=4$是原方程的解.
答:AP 的长为4m.