第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1[2024广东河源质检]如图是一个正八边形,则它(
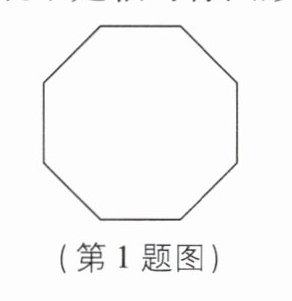
A.只是轴对称图形
B.只是中心对称图形
C.既是轴对称图形,也是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
C
)
A.只是轴对称图形
B.只是中心对称图形
C.既是轴对称图形,也是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
答案:
C 【解析】正八边形既是轴对称图形,也是中心对称图形. 故选 C.
2如图,正六边形的面积为6a,则图中阴影部分的面积为____.
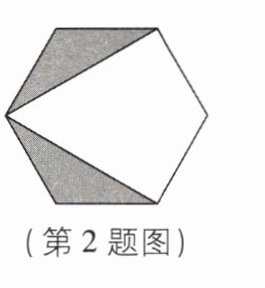

答案:
2a 【解析】如图,连接 AD,BE,CF 交于点 O.
∵ 六边形 ABCDEF 是正六边形,
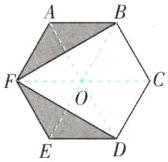
∴ CF//AB//DE,
∴ S△ABF=S△AOB = $\frac{1}{6}$S正六边形ABCDEF,S△DEF = S△EOD = $\frac{1}{6}$S正六边形ABCDEF,
∴ S阴影 = $\frac{1}{3}$S正六边形ABCDEF=2a.
2a 【解析】如图,连接 AD,BE,CF 交于点 O.
∵ 六边形 ABCDEF 是正六边形,

∴ CF//AB//DE,
∴ S△ABF=S△AOB = $\frac{1}{6}$S正六边形ABCDEF,S△DEF = S△EOD = $\frac{1}{6}$S正六边形ABCDEF,
∴ S阴影 = $\frac{1}{3}$S正六边形ABCDEF=2a.
3我们可以只用直尺和圆规作出圆的部分内接正多边形.在我们目前所学知识的范围内,下列圆的内接正多边形不可以用尺规作图作出的是(
A.正三角形
B.正四边形
C.正六边形
D.正七边形
D
)A.正三角形
B.正四边形
C.正六边形
D.正七边形
答案:
D 【解析】取圆上一点为圆心,以已知圆的半径为半径画弧,与已知圆交于一点,以该点为圆心,按上述方法画弧,重复此种作法可得到圆的六等分点,据此可得圆的内接正六边形;在以上所得六等分点中,间隔取点,首尾连接可得圆的内接正三角形;由于圆的直径可以将圆二等分、两条互相垂直的直径可以将圆四等分,据此可作出圆的内接正四边形.综上可知,不可以用尺规作图作出的是圆的内接正七边形,故选 D.
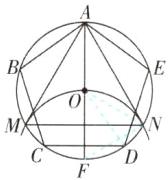
4[2025江苏苏州期末]如图,正五边形ABCDE内接于$\odot O$,阅读以下作图过程:
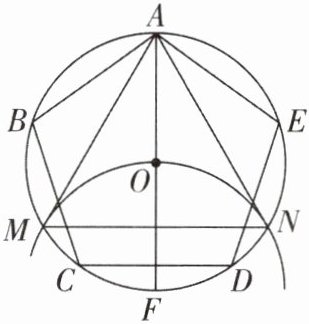
①作直径AF;
②以点F为圆心,FO为半径作圆弧,与$\odot O$交于点M,N;
③连接AM,MN,AN.
结论Ⅰ:$\triangle AMN$是等边三角形;
结论Ⅱ:从点A开始,以DN长为半径,在$\odot O$上依次截取点,再依次连接这些点,可以得到正十八边形.
对于结论Ⅰ和结论Ⅱ,下列判断正确的是( )
A.结论Ⅰ和结论Ⅱ都正确
B.结论Ⅰ和结论Ⅱ都错误
C.结论Ⅰ错误,结论Ⅱ正确
D.结论Ⅰ正确,结论Ⅱ错误

①作直径AF;
②以点F为圆心,FO为半径作圆弧,与$\odot O$交于点M,N;
③连接AM,MN,AN.
结论Ⅰ:$\triangle AMN$是等边三角形;
结论Ⅱ:从点A开始,以DN长为半径,在$\odot O$上依次截取点,再依次连接这些点,可以得到正十八边形.
对于结论Ⅰ和结论Ⅱ,下列判断正确的是( )
A.结论Ⅰ和结论Ⅱ都正确
B.结论Ⅰ和结论Ⅱ都错误
C.结论Ⅰ错误,结论Ⅱ正确
D.结论Ⅰ正确,结论Ⅱ错误
答案:
D 【解析】结论Ⅰ:如图,连接 ON,FN. 由作图可知,FN=FO.
∵ ON=OF,
∴ ON=OF=FN,
∴ △OFN 是等边三角形,
∴ ∠OFN=60°,
∴ ∠AMN=∠OFN = 60°,同理,
∠ANM=60°,
∴ ∠ANM=∠AMN=∠NAM=60°,
∴ △AMN是等边三角形,
∴ 结论Ⅰ正确;结论Ⅱ:如图,连接 OD.
∵ ∠AMN=60°,
∴ ∠AON=2∠AMN=120°.
∵ $\widehat{AD}=2\widehat{AE}$,多边形 ABCDE 为正五边形,
∴ ∠AOD=2×72°=144°,
∴ ∠NOD=∠AOD - ∠AON=144° - 120°=24°,
∴ 可以得到的正多边形的边数是$\frac{360^\circ}{24^\circ}=15$,
∴ 结论Ⅱ错误. 故选 D.
D 【解析】结论Ⅰ:如图,连接 ON,FN. 由作图可知,FN=FO.
∵ ON=OF,
∴ ON=OF=FN,
∴ △OFN 是等边三角形,
∴ ∠OFN=60°,
∴ ∠AMN=∠OFN = 60°,同理,

∠ANM=60°,
∴ ∠ANM=∠AMN=∠NAM=60°,
∴ △AMN是等边三角形,
∴ 结论Ⅰ正确;结论Ⅱ:如图,连接 OD.
∵ ∠AMN=60°,
∴ ∠AON=2∠AMN=120°.
∵ $\widehat{AD}=2\widehat{AE}$,多边形 ABCDE 为正五边形,
∴ ∠AOD=2×72°=144°,
∴ ∠NOD=∠AOD - ∠AON=144° - 120°=24°,
∴ 可以得到的正多边形的边数是$\frac{360^\circ}{24^\circ}=15$,
∴ 结论Ⅱ错误. 故选 D.
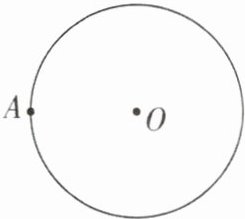
5已知$\odot O和\odot O$上的一点A.
(1)作$\odot O$的内接正方形ABCD和内接正六边形AEFCGH(写出作法,保留作图痕迹).
(2)在(1)题的作图中,如果点E在弧AD上,求证:DE是$\odot O$内接正十二边形的一边.
(1)作$\odot O$的内接正方形ABCD和内接正六边形AEFCGH(写出作法,保留作图痕迹).
(2)在(1)题的作图中,如果点E在弧AD上,求证:DE是$\odot O$内接正十二边形的一边.

答案:
(1)【解】如图所示,即为所作. 作法:①连接 AO 并延长,交⊙O于另一点 C;②作 AC 的垂直平分线,交⊙O于点 B,D;
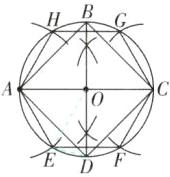
③顺次连接 A,B,C,D 四点. 四边形 ABCD 即为⊙O的内接正方形.④分别以 A,C 为圆心,以 OA 长为半径作弧,交⊙O于点 E,H,F,G;⑤顺次连接 A,E,F,C,G,H 各点. 六边形 AEFCGH 即为⊙O的内接正六边形.
(2)【证明】连接 OE,DE,如图.
∵ ∠AOD=$\frac{360^\circ}{4}=90^\circ$,∠AOE=$\frac{360^\circ}{6}=60^\circ$,
∴ ∠DOE=∠AOD - ∠AOE=90° - 60°=30°.
∵ $\frac{360^\circ}{30^\circ}=12$,
∴ DE 为⊙O的内接正十二边形的一边.
(1)【解】如图所示,即为所作. 作法:①连接 AO 并延长,交⊙O于另一点 C;②作 AC 的垂直平分线,交⊙O于点 B,D;

③顺次连接 A,B,C,D 四点. 四边形 ABCD 即为⊙O的内接正方形.④分别以 A,C 为圆心,以 OA 长为半径作弧,交⊙O于点 E,H,F,G;⑤顺次连接 A,E,F,C,G,H 各点. 六边形 AEFCGH 即为⊙O的内接正六边形.
(2)【证明】连接 OE,DE,如图.
∵ ∠AOD=$\frac{360^\circ}{4}=90^\circ$,∠AOE=$\frac{360^\circ}{6}=60^\circ$,
∴ ∠DOE=∠AOD - ∠AOE=90° - 60°=30°.
∵ $\frac{360^\circ}{30^\circ}=12$,
∴ DE 为⊙O的内接正十二边形的一边.
6试用正多边形知识解答下列问题:
(1)如图(1),正五边形ABCDE中,连接AC,BE交于点G,求证:四边形GCDE是菱形.
(2)如图(2)是一个斜网格图(8×8),每个小菱形的较小内角是$72^{\circ }$,请利用一把角尺(只能画直角和直线,不能度量,可以用三角板替代)在斜网格图中画出以AB为一边的正五边形ABCDE(保留作图痕迹).
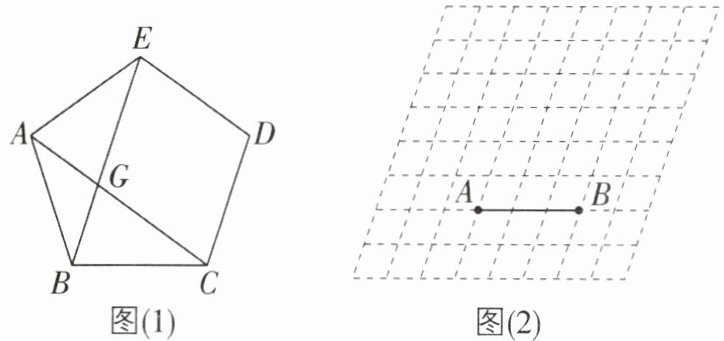
(1)如图(1),正五边形ABCDE中,连接AC,BE交于点G,求证:四边形GCDE是菱形.
(2)如图(2)是一个斜网格图(8×8),每个小菱形的较小内角是$72^{\circ }$,请利用一把角尺(只能画直角和直线,不能度量,可以用三角板替代)在斜网格图中画出以AB为一边的正五边形ABCDE(保留作图痕迹).

答案:
(1)【证明】
∵ 五边形 ABCDE 是正五边形,
∴ ∠ABC=∠BCD=∠CDE=∠DEA=∠EAB=108°,AB=BC=CD=DE=AE,
∴ ∠BCA=36°,∠BEA=36°,
∴ ∠ACD=72°,∠DEB=72°,
∴ ∠ACD+∠CDE=180°,∠DEB+∠CDE=180°,
∴ AC//ED,BE//CD,
∴ 四边形 GCDE 是平行四边形. 又
∵ CD=DE,
∴ 四边形 GCDE 是菱形.
(2)【解】(作法不唯一)如图所示,先画菱形 ABCH,连接对角线 AC,BH,过对角线的交点作 AB,BC 的平行线,再过平行线与 AB,BC 的交点,作 AB 的垂线交直线 AH 于 D,作 BC 的垂线交直线 CH 于 E,顺次连接各点,正五边形 ABCDE 即为所求.

(1)【证明】
∵ 五边形 ABCDE 是正五边形,
∴ ∠ABC=∠BCD=∠CDE=∠DEA=∠EAB=108°,AB=BC=CD=DE=AE,
∴ ∠BCA=36°,∠BEA=36°,
∴ ∠ACD=72°,∠DEB=72°,
∴ ∠ACD+∠CDE=180°,∠DEB+∠CDE=180°,
∴ AC//ED,BE//CD,
∴ 四边形 GCDE 是平行四边形. 又
∵ CD=DE,
∴ 四边形 GCDE 是菱形.
(2)【解】(作法不唯一)如图所示,先画菱形 ABCH,连接对角线 AC,BH,过对角线的交点作 AB,BC 的平行线,再过平行线与 AB,BC 的交点,作 AB 的垂线交直线 AH 于 D,作 BC 的垂线交直线 CH 于 E,顺次连接各点,正五边形 ABCDE 即为所求.

查看更多完整答案,请扫码查看


