《2025年初中必刷题九年级数学上册苏科版》

1 [中]如图,将扇形 AOB 翻折,使点 A 与圆心 O 重合,展开后折痕所在直线 l 与$\overset{\frown}{AB}$交于点 C,连接 AC. 若$OA = 2$,则图中阴影部分的面积是(B)
A.$\frac{2\pi}{3}-\frac{\sqrt{3}}{2}$
B.$\frac{2\pi}{3}-\sqrt{3}$
C.$\frac{\pi}{3}-\frac{\sqrt{3}}{2}$
D.$\frac{\pi}{3}$

答案： B

如图,在$3×3$的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中的圆弧为格点$△ABC$外接圆的一部分,小正方形边长为 1,则图中阴影部分的面积为(D)
A.$\frac{5}{2}\pi-\frac{7}{4}$
B.$\frac{5}{2}\pi-\frac{7}{2}$
C.$\frac{5}{4}\pi-\frac{7}{4}$
D.$\frac{5}{4}\pi-\frac{7}{2}$

答案： D

3 [中]如图,四边形 ABCD 是边长为$\frac{1}{2}$的正方形,曲线$DA_{1}B_{1}C_{1}D_{1}A_{2}…是由多段90^{\circ}$的圆心角所对的弧组成的. 其中,$\overset{\frown}{DA_{1}}$的圆心为 A,半径为 AD；$\overset{\frown}{A_{1}B_{1}}$的圆心为 B,半径为$BA_{1}$；…；$\overset{\frown}{DA_{1}}$,$\overset{\frown}{A_{1}B_{1}}$,…的圆心依次按点 A,B,C,D 为一组进行循环,则$\overset{\frown}{C_{2022}D_{2022}}$的长是______2022π(结果保留$\pi$).

答案： 2022π

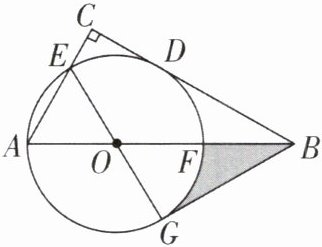
4 [2025 江苏南通质检,中]如图,在$Rt△ABC$中,$∠ACB = 90^{\circ}$,点 F 在 AB 上,以 AF 为直径的$\odot O$与边 BC 相切于点 D,与边 AC 相交于点 E,且$\overset{\frown}{AE}= \overset{\frown}{DE}$,连接 EO 并延长交$\odot O$于点 G,连接 BG.
(1)求证：BG 是$\odot O$的切线；
(2)若$\overset{\frown}{DE}的长为\frac{4}{3}\pi$,求图中阴影部分的面积.

答案：
(1)【证明】如图，连接OD。
∵⊙O与BC相切于点D，
∴∠ODB = 90°。
∵∠ACB = 90°，
∴∠ACB = ∠ODB，
∴AC// OD，
∴∠EOD = ∠AEO。
∵$\overset{\frown}{AE}=\overset{\frown}{DE}，$
∴∠EOD = ∠AOE，
∴∠AOE = ∠AEO，
∴AO = AE。又
∵AO = OE，
∴AO = OE = AE，
∴△AOE是等边三角形，
∴∠AOE = 60°，
∴∠BOG = ∠AOE = 60°，
∴∠DOB = 180°-∠DOE-∠AOE = 60°，
∴∠DOB = ∠GOB。
∵OD = OG，OB = OB，
∴△ODB≌△OGB(SAS)，
∴∠OGB = ∠ODB = 90°，
∴OG⊥BG。
∵OG为⊙O半径，
∴BG是⊙O的切线。
(2)【解】
∵$\overset{\frown}{DE}$的长为$\frac{4}{3}\pi，$∠DOE = 60°，
∴$\frac{60×\pi× OD}{180}=\frac{4}{3}\pi，$
∴OD = 4，
∴OG = 4。
∵∠BOG = 60°，
∴∠OBG = 30°，易得$BG = 4\sqrt{3}，$
∴$S_{\triangle OBG}=\frac{1}{2}OG× BG=\frac{1}{2}× 4× 4\sqrt{3}=8\sqrt{3}，$$S_{扇形GOF}=\frac{60×\pi× 4^{2}}{360}=\frac{8}{3}\pi，$
∴$S_{阴影}=S_{\triangle OGB}-S_{扇形GOF}=8\sqrt{3}-\frac{8}{3}\pi。$

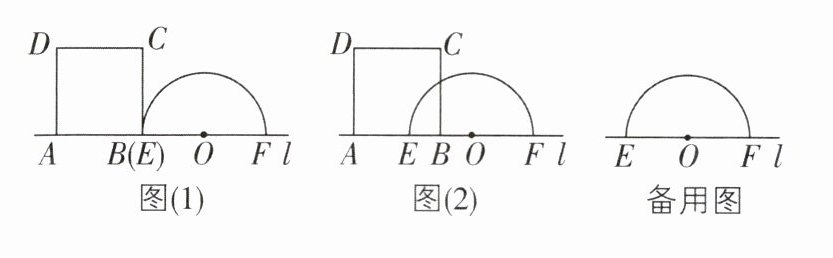
5 [较难]如图(1),矩形 ABCD 与以 EF 为直径的半圆 O 在直线 l 的上方,线段 AB 与点 E,F 都在直线 l 上,且$AB = 7$,$EF = 10$,$BC＞5$. 点 B 以 1 个单位/秒的速度从点 E 处出发,沿射线 EF 方向运动,矩形 ABCD 随之运动,运动时间为 t 秒.
(1)如图(2),当$t = 2.5$时,求半圆 O 在矩形 ABCD 内的弧的长度；
(2)在点 B 运动的过程中,当 AD,BC 都与半圆 O 相交时,设这两个交点为 G,H,连接 OG,OH. 若$∠GOH$为直角,求此时 t 的值.

答案：
(1)【解】如图
(1)，设BC与半圆O交于点M，连接OM，EM。当t = 2.5时，BE = 2.5。
∵EF = 10，
∴$OE=\frac{1}{2}EF = 5，$
∴OB = 2.5，
∴EB = OB。在矩形ABCD中，∠ABC = 90°，
∴ME = MO。又
∵MO = EO，
∴ME = EO = MO，
∴△MOE是等边三角形，
∴∠EOM = 60°，
∴$l_{\overset{\frown}{ME}}=\frac{60\pi× 5}{180}=\frac{5\pi}{3}，$即半圆O在矩形ABCD内的弧的长度为$\frac{5\pi}{3}。$
(2)【解】如图
(2)。
∵∠GOH = 90°，
∴∠AOG + ∠BOH = 90°。
∵∠AGO + ∠AOG = 90°，
∴∠AGO = ∠BOH。在△AGO和△BOH中，$\begin{cases}\angle AGO = \angle BOH\\\angle GAO = \angle HBO\\OG = OH\end{cases}，$
∴△AGO≌△BOH(AAS)，
∴OB = AG = t - 5。
∵AB = 7，
∴AE = t - 7，
∴AO = 5 - (t - 7)=12 - t。在Rt△AGO中，AG²+AO²=OG²，
∴(t - 5)²+(12 - t)²=5²，解得t₁=8，t₂=9，即t的值为8或9。