第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1[2025江苏常州调研]如图,将三块完全相同的等腰直角三角板的一个锐角顶点都放在点M处,再使其各有一条直角边恰好在△ABC的边上,此时点M是(
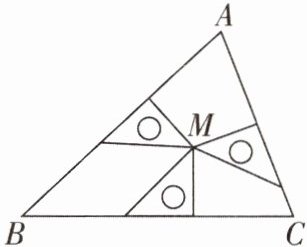
A.△ABC的外心
B.△ABC的内心
C.△ABC的重心
D.△ABC的垂心
B
)
A.△ABC的外心
B.△ABC的内心
C.△ABC的重心
D.△ABC的垂心
答案:
B 【解析】根据题意可得点M到AB,BC,AC的距离相等,都为等腰直角三角形的腰长,
∴点M是△ABC的内心. 故选B.
∴点M是△ABC的内心. 故选B.
2下列说法:①三角形的内心不一定在三角形的内部;②若点I是△ABC的内心,则AI平分∠BAC;③三角形有唯一的内切圆,圆有唯一的外切三角形.其中正确的有
1
个.
答案:
1 【解析】三角形的内心是三角形三条角平分线的交点,内心一定在三角形的内部,故①错误,②正确;圆的外切三角形有无数个,故③错误.
3如图,已知等边三角形ABC的内切圆⊙O半径为3,则AB的长为( )
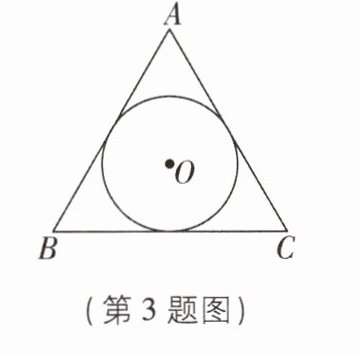
A.3√3
B.3√5
C.6√3
D.6√5

A.3√3
B.3√5
C.6√3
D.6√5
答案:
C 【解析】如图,过O点作OD⊥BC交BC于点D,连接OB,则OD=3.
∵O是△ABC的内心,
∴∠OBD= $\frac{1}{2}$∠ABC=30°,BD=CD. 在Rt△OBD中,∠OBD=30°,OD=3,
∴OB=6,
∴BD= $3\sqrt{3}$,
∴AB=BC=2BD= $6\sqrt{3}$. 故选C.

C 【解析】如图,过O点作OD⊥BC交BC于点D,连接OB,则OD=3.
∵O是△ABC的内心,
∴∠OBD= $\frac{1}{2}$∠ABC=30°,BD=CD. 在Rt△OBD中,∠OBD=30°,OD=3,
∴OB=6,
∴BD= $3\sqrt{3}$,
∴AB=BC=2BD= $6\sqrt{3}$. 故选C.

4[2024江苏淮安调研]如图,点O是△ABC的内心,也是△DBC的外心.若∠A= 84°,则∠D的度数为(

A.42°
B.66°
C.76°
D.82°
B
)
A.42°
B.66°
C.76°
D.82°
答案:
B 【解析】连接OB,OC.
∵点O是△ABC的内心,∠A=84°,
∴OB,OC分别是∠ABC,∠ACB的平分线,
∴∠OBC= $\frac{1}{2}$∠ABC,∠OCB= $\frac{1}{2}$∠ACB,
∴∠BOC=180°-∠OBC-∠OCB=180°- $\frac{1}{2}$(∠ABC+∠ACB)=180°- $\frac{1}{2}$(180°-∠A)=90°+ $\frac{1}{2}$∠A=132°.
∵点O也是△DBC的外心,
∴∠D= $\frac{1}{2}$∠BOC=66°. 故选B.
∵点O是△ABC的内心,∠A=84°,
∴OB,OC分别是∠ABC,∠ACB的平分线,
∴∠OBC= $\frac{1}{2}$∠ABC,∠OCB= $\frac{1}{2}$∠ACB,
∴∠BOC=180°-∠OBC-∠OCB=180°- $\frac{1}{2}$(∠ABC+∠ACB)=180°- $\frac{1}{2}$(180°-∠A)=90°+ $\frac{1}{2}$∠A=132°.
∵点O也是△DBC的外心,
∴∠D= $\frac{1}{2}$∠BOC=66°. 故选B.
5[2025浙江杭州质检]如图,平面直角坐标系中三个点的坐标为A(1,1),B(2,4),C(3,1),则△ABC的内切圆的半径长为______.
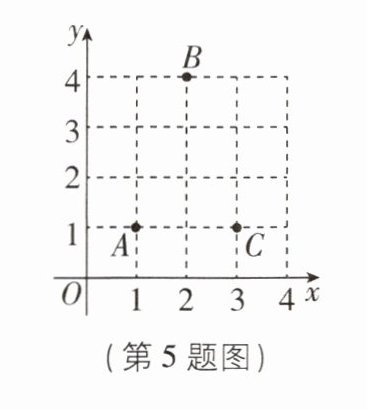

答案:
$\frac{\sqrt{10}-1}{3}$ 【解析】如图,设△ABC的内切圆⊙I与AB,BC,AC分别相切于点F,J,E.
∵A(1,1),B(2,4),C(3,1),
∴AC=2,AB= $\sqrt{(2-1)^2+(4-1)^2}$= $\sqrt{10}$,BC= $\sqrt{(3-2)^2+(1-4)^2}$= $\sqrt{10}$,
∴AB=CB,$S_{\triangle ABC}$= $\frac{1}{2}×2×3=3$. 连接AI,BI,CI,设△ABC的内切圆的半径长为r,则IF=IJ=IE=r.
∵IF⊥AB,IJ⊥BC,IE⊥AC,
∴$S_{\triangle ABC}=S_{\triangle ABI}+S_{\triangle ACI}+S_{\triangle BCI}$= $\frac{1}{2}×\sqrt{10}× r+\frac{1}{2}×2× r+\frac{1}{2}×\sqrt{10}× r=3$,解得r= $\frac{\sqrt{10}-1}{3}$,故答案为 $\frac{\sqrt{10}-1}{3}$.

$\frac{\sqrt{10}-1}{3}$ 【解析】如图,设△ABC的内切圆⊙I与AB,BC,AC分别相切于点F,J,E.
∵A(1,1),B(2,4),C(3,1),
∴AC=2,AB= $\sqrt{(2-1)^2+(4-1)^2}$= $\sqrt{10}$,BC= $\sqrt{(3-2)^2+(1-4)^2}$= $\sqrt{10}$,
∴AB=CB,$S_{\triangle ABC}$= $\frac{1}{2}×2×3=3$. 连接AI,BI,CI,设△ABC的内切圆的半径长为r,则IF=IJ=IE=r.
∵IF⊥AB,IJ⊥BC,IE⊥AC,
∴$S_{\triangle ABC}=S_{\triangle ABI}+S_{\triangle ACI}+S_{\triangle BCI}$= $\frac{1}{2}×\sqrt{10}× r+\frac{1}{2}×2× r+\frac{1}{2}×\sqrt{10}× r=3$,解得r= $\frac{\sqrt{10}-1}{3}$,故答案为 $\frac{\sqrt{10}-1}{3}$.

6[2025江苏无锡调研]如图,点I是△ABC的内心,连接IB,IC.
(1)若∠A= 90°,则∠BIC的度数为______;
(2)连接IA,则S△IBC______S△IAB+S△IAC(填“<”“=”或“>”).
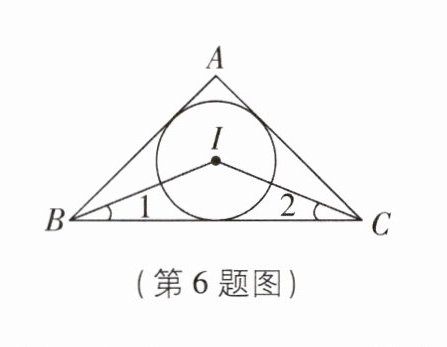
(1)若∠A= 90°,则∠BIC的度数为______;
(2)连接IA,则S△IBC______S△IAB+S△IAC(填“<”“=”或“>”).

答案:
(1)135°
(2)< 【解析】
(1)
∵∠A=90°,
∴∠ABC+∠ACB=90°.
∵点I是△ABC的内心,
∴IB,IC是△ABC的角平分线,
∴∠1= $\frac{1}{2}$∠ABC,∠2= $\frac{1}{2}$∠ACB,
∴∠1+∠2= $\frac{1}{2}$(∠ABC+∠ACB)=45°,
∴∠BIC=180°-∠1-∠2=135°. 故答案为135°.
(2)如图所示.
∵点I是△ABC的内心,
∴点I是△ABC的三条角平分线的交点,
∴点I到△ABC三边的距离相等. 设点I到△ABC三边的距离为h,则$S_{\triangle IBC}$= $\frac{1}{2}BC\cdot h$,$S_{\triangle IAB}+S_{\triangle IAC}$= $\frac{1}{2}AB\cdot h+\frac{1}{2}AC\cdot h$= $\frac{1}{2}(AB+AC)\cdot h$.
∵BC<AC+AB,
∴$S_{\triangle IBC}<S_{\triangle IAB}+S_{\triangle IAC}$. 故答案为<.

(1)135°
(2)< 【解析】
(1)
∵∠A=90°,
∴∠ABC+∠ACB=90°.
∵点I是△ABC的内心,
∴IB,IC是△ABC的角平分线,
∴∠1= $\frac{1}{2}$∠ABC,∠2= $\frac{1}{2}$∠ACB,
∴∠1+∠2= $\frac{1}{2}$(∠ABC+∠ACB)=45°,
∴∠BIC=180°-∠1-∠2=135°. 故答案为135°.
(2)如图所示.
∵点I是△ABC的内心,
∴点I是△ABC的三条角平分线的交点,
∴点I到△ABC三边的距离相等. 设点I到△ABC三边的距离为h,则$S_{\triangle IBC}$= $\frac{1}{2}BC\cdot h$,$S_{\triangle IAB}+S_{\triangle IAC}$= $\frac{1}{2}AB\cdot h+\frac{1}{2}AC\cdot h$= $\frac{1}{2}(AB+AC)\cdot h$.
∵BC<AC+AB,
∴$S_{\triangle IBC}<S_{\triangle IAB}+S_{\triangle IAC}$. 故答案为<.

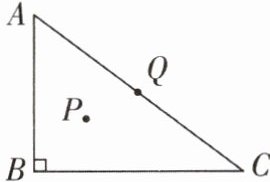
7如图,已知在Rt△ABC中,∠B= 90°,AB= 6,AC= 10,点P是Rt△ABC的内心.
(1)点P到边AB的距离为______;
(2)点Q是Rt△ABC的外心,连接PQ,求PQ的长.
(1)点P到边AB的距离为______;
(2)点Q是Rt△ABC的外心,连接PQ,求PQ的长.

答案:
(1)2 【解析】如图,连接AP,BP,CP,过点P分别作PD⊥AB,PF⊥AC,PE⊥BC,垂足分别为D,F,E.在Rt△ABC中,
∵∠ABC=90°,AB=6,AC=10,
∴BC= $\sqrt{AC^2-AB^2}$=8.
∵点P是Rt△ABC的内心,
∴PD=PE=PF.
∵$S_{\triangle ABC}$= $\frac{1}{2}BC\cdot AB$= $\frac{1}{2}×8×6=24$,
∴$\frac{1}{2}× PD×6+\frac{1}{2}× PE×8+\frac{1}{2}× PF×10=24$,
∴PD=2,
∴点P到边AB的距离为2. 故答案为2.
(2)如图,由
(1)知,PD=PE=2.
∵PE⊥BC,PD⊥AB,∠ABC=90°,
∴四边形BEPD是正方形,
∴BE=BD=PD=PE=2.
∵AB=6,
∴AD=4.
∵点P是Rt△ABC的内心,
∴∠DAP=∠FAP. 在△ADP和△AFP中,$\begin{cases}\angle DAP=\angle FAP,\\\angle ADP=\angle AFP=90^{\circ},\\AP=AP,\end{cases}$
∴△ADP≌△AFP(AAS),
∴AD=AF=4.
∵Q是Rt△ABC的外心,
∴AQ=5,
∴FQ=1. 在Rt△FPQ中,根据勾股定理得PQ= $\sqrt{PF^2+FQ^2}=\sqrt{2^2+1^2}=\sqrt{5}$.

(1)2 【解析】如图,连接AP,BP,CP,过点P分别作PD⊥AB,PF⊥AC,PE⊥BC,垂足分别为D,F,E.在Rt△ABC中,
∵∠ABC=90°,AB=6,AC=10,
∴BC= $\sqrt{AC^2-AB^2}$=8.
∵点P是Rt△ABC的内心,
∴PD=PE=PF.
∵$S_{\triangle ABC}$= $\frac{1}{2}BC\cdot AB$= $\frac{1}{2}×8×6=24$,
∴$\frac{1}{2}× PD×6+\frac{1}{2}× PE×8+\frac{1}{2}× PF×10=24$,
∴PD=2,
∴点P到边AB的距离为2. 故答案为2.
(2)如图,由
(1)知,PD=PE=2.
∵PE⊥BC,PD⊥AB,∠ABC=90°,
∴四边形BEPD是正方形,
∴BE=BD=PD=PE=2.
∵AB=6,
∴AD=4.
∵点P是Rt△ABC的内心,
∴∠DAP=∠FAP. 在△ADP和△AFP中,$\begin{cases}\angle DAP=\angle FAP,\\\angle ADP=\angle AFP=90^{\circ},\\AP=AP,\end{cases}$
∴△ADP≌△AFP(AAS),
∴AD=AF=4.
∵Q是Rt△ABC的外心,
∴AQ=5,
∴FQ=1. 在Rt△FPQ中,根据勾股定理得PQ= $\sqrt{PF^2+FQ^2}=\sqrt{2^2+1^2}=\sqrt{5}$.

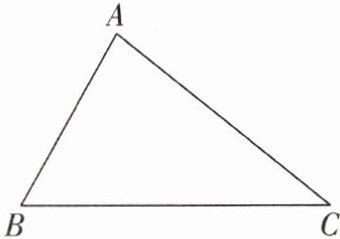
8[2025江苏淮安调研]已知△ABC,如图所示.
(1)用无刻度直尺和圆规作出△ABC内切圆的圆心O.(保留作图痕迹,不写作法和证明)
(2)如果△ABC的周长为14cm,内切圆的半径为1.2cm,求△ABC的面积.
(1)用无刻度直尺和圆规作出△ABC内切圆的圆心O.(保留作图痕迹,不写作法和证明)
(2)如果△ABC的周长为14cm,内切圆的半径为1.2cm,求△ABC的面积.

答案:
(1)如图所示,O为所求作的点.

(2)如图所示,连接OA,OB,OC,作OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为点D,E,F.
∵内切圆的半径为1.2 cm,
∴OD=OF=OE=1.2 cm.
∵△ABC的周长为14 cm,
∴AB+BC+AC=14 cm,则$S_{\triangle ABC}=S_{\triangle AOB}+S_{\triangle COB}+S_{\triangle AOC}$= $\frac{1}{2}\cdot AB\cdot OD+\frac{1}{2}\cdot BC\cdot OE+\frac{1}{2}\cdot AC\cdot OF$= $\frac{1}{2}×1.2×(AB+BC+AC)=\frac{1}{2}×1.2×14=8.4(cm^2)$. 故△ABC的面积为8.4 cm².
归纳总结 求△ABC内切圆的半径可以用r= $\frac{2S_{\triangle ABC}}{C_{\triangle ABC}}$来求.
关键点拨
(1)作△ABC内切圆的圆心,只需作△ABC任意两内角的平分线,找到两条角平分线的交点即可.
(1)如图所示,O为所求作的点.

(2)如图所示,连接OA,OB,OC,作OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为点D,E,F.
∵内切圆的半径为1.2 cm,
∴OD=OF=OE=1.2 cm.
∵△ABC的周长为14 cm,
∴AB+BC+AC=14 cm,则$S_{\triangle ABC}=S_{\triangle AOB}+S_{\triangle COB}+S_{\triangle AOC}$= $\frac{1}{2}\cdot AB\cdot OD+\frac{1}{2}\cdot BC\cdot OE+\frac{1}{2}\cdot AC\cdot OF$= $\frac{1}{2}×1.2×(AB+BC+AC)=\frac{1}{2}×1.2×14=8.4(cm^2)$. 故△ABC的面积为8.4 cm².
归纳总结 求△ABC内切圆的半径可以用r= $\frac{2S_{\triangle ABC}}{C_{\triangle ABC}}$来求.
关键点拨
(1)作△ABC内切圆的圆心,只需作△ABC任意两内角的平分线,找到两条角平分线的交点即可.
查看更多完整答案,请扫码查看


