第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1 [2023 湖北孝感中考]如图, 在$\odot O$中, 直径$AB与弦CD相交于点P$, 连接$AC,AD,BD$, 若$∠C = 20^{\circ},∠BPC = 70^{\circ}$, 则$∠ADC = $ (
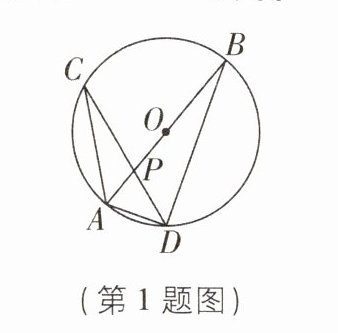
A.$70^{\circ}$
B.$60^{\circ}$
C.$50^{\circ}$
D.$40^{\circ}$
D
)
A.$70^{\circ}$
B.$60^{\circ}$
C.$50^{\circ}$
D.$40^{\circ}$
答案:
1.D 【解析】
∵∠C=20°,∠BPC=70°,
∴∠BAC=∠BPC - ∠C=50°=∠BDC.
∵AB 是⊙O 的直径,
∴∠ADB=90°,
∴∠ADC=∠ADB - ∠BDC=40°,故选 D.
∵∠C=20°,∠BPC=70°,
∴∠BAC=∠BPC - ∠C=50°=∠BDC.
∵AB 是⊙O 的直径,
∴∠ADB=90°,
∴∠ADC=∠ADB - ∠BDC=40°,故选 D.
2 [2025 江苏南京调研]如图,$AB是半圆O$的直径,$C$是半圆上的点,$D是\widehat {AC}$上的点. 连接$AC,AD,CD$, 若$∠BAC = 20^{\circ}$, 则$∠D$的度数为( )
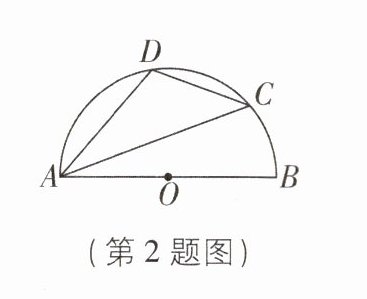
A.$100^{\circ}$
B.$110^{\circ}$
C.$120^{\circ}$
D.$130^{\circ}$

A.$100^{\circ}$
B.$110^{\circ}$
C.$120^{\circ}$
D.$130^{\circ}$
答案:
2.B 【解析】连接 BD,如图.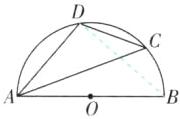
∵AB 是半圆 O 的直径,
∴∠ADB=90°.
∵∠BAC=20°,
∴∠BDC=∠BAC=20°,
∴∠ADC=∠ADB + ∠BDC=90° + 20°=110°.故选 B.
2.B 【解析】连接 BD,如图.

∵AB 是半圆 O 的直径,
∴∠ADB=90°.
∵∠BAC=20°,
∴∠BDC=∠BAC=20°,
∴∠ADC=∠ADB + ∠BDC=90° + 20°=110°.故选 B.
3 [2024 江苏无锡调研]如图,$AB为\odot O$的直径,点$C$为圆上一点,将劣弧$AC沿弦AC翻折交AB于点D$, 连接$CD$, 点$D与圆心O$不重合,$∠BAC = 26^{\circ}$, 则$∠DCA$的度数为____.
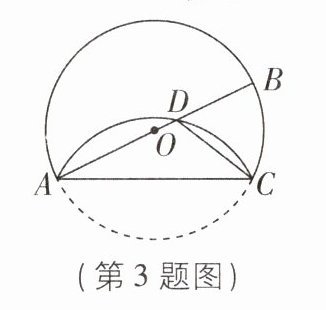

答案:
3.38° 【解析】如图,连接 BC.
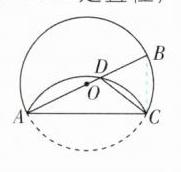
∵AB 是直径,
∴∠ACB=90°.
∵∠BAC=26°,
∴∠B=90° - ∠BAC=90° - 26°=64°.
∵$\overset{\frown}{AC}$所对的圆周角为∠B,
∴$\overset{\frown}{ABC}$所对的圆周角为 180° - ∠B=116°.由翻折的性质得∠ADC=116°,
∴∠BDC=64°,
∴∠DCA=∠BDC - ∠BAC=64° - 26°=38°,故答案为 38°.
3.38° 【解析】如图,连接 BC.

∵AB 是直径,
∴∠ACB=90°.
∵∠BAC=26°,
∴∠B=90° - ∠BAC=90° - 26°=64°.
∵$\overset{\frown}{AC}$所对的圆周角为∠B,
∴$\overset{\frown}{ABC}$所对的圆周角为 180° - ∠B=116°.由翻折的性质得∠ADC=116°,
∴∠BDC=64°,
∴∠DCA=∠BDC - ∠BAC=64° - 26°=38°,故答案为 38°.
4 [2025 黑龙江哈尔滨调研]如图,$AB是\odot O$的弦,半径$OD⊥AB于点C$,$AE$为直径,$AB = 8$,$CD = 2$, 则线段$CE$的长为____.
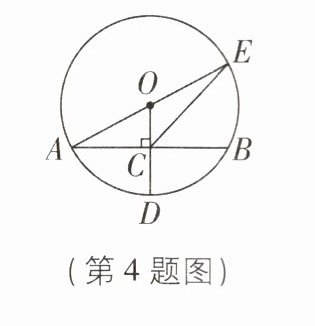

答案:
4.$2\sqrt{13}$ 【解析】连接 BE,如图.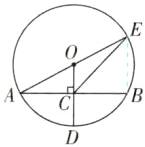
∵AB 是⊙O 的弦,半径 OD⊥AB 于点 C,
∴AC=BC=$\frac{1}{2}$AB=4.在 Rt△AOC 中,AO² = OC² + AC²=(OD - 2)² + 4²=(OA - 2)² + 16,解得 AO = 5.
∵O,C 分别是 AE,AB 的中点,
∴OC 是△ABE 的中位线,
∴BE=2OC=2×(5 - 2)=6.
∵AE 为⊙O 的直径,
∴∠ABE=90°.在 Rt△CBE 中,CE=$\sqrt{CB^{2}+BE^{2}}$=$\sqrt{4^{2}+6^{2}}$=$2\sqrt{13}$.故答案为$2\sqrt{13}$.
4.$2\sqrt{13}$ 【解析】连接 BE,如图.

∵AB 是⊙O 的弦,半径 OD⊥AB 于点 C,
∴AC=BC=$\frac{1}{2}$AB=4.在 Rt△AOC 中,AO² = OC² + AC²=(OD - 2)² + 4²=(OA - 2)² + 16,解得 AO = 5.
∵O,C 分别是 AE,AB 的中点,
∴OC 是△ABE 的中位线,
∴BE=2OC=2×(5 - 2)=6.
∵AE 为⊙O 的直径,
∴∠ABE=90°.在 Rt△CBE 中,CE=$\sqrt{CB^{2}+BE^{2}}$=$\sqrt{4^{2}+6^{2}}$=$2\sqrt{13}$.故答案为$2\sqrt{13}$.
5 如图, 在$\odot O$中, 弦$AB⊥CD$, 连接$AD,BC$,$BC = 2$,$AD = 6$, 则$\odot O$的直径长为____.
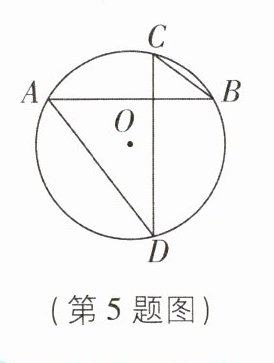

答案:
5.$2\sqrt{10}$ 【解析】如图,连接 AO,延长 AO 交⊙O 于点 H,连接 BH,DH,BD.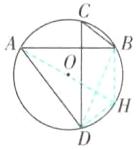
∵AH 是直径,
∴∠ABH=∠ADH=90°,
∴AB⊥BH.
∵AB⊥CD,
∴CD//BH,
∴∠CDB=∠DBH,
∴$\overset{\frown}{BC}$=$\overset{\frown}{DH}$,
∴DH=BC=2,
∴AH=$\sqrt{AD^{2}+DH^{2}}$=$\sqrt{6^{2}+2^{2}}$=$2\sqrt{10}$.故答案为$2\sqrt{10}$.
5.$2\sqrt{10}$ 【解析】如图,连接 AO,延长 AO 交⊙O 于点 H,连接 BH,DH,BD.

∵AH 是直径,
∴∠ABH=∠ADH=90°,
∴AB⊥BH.
∵AB⊥CD,
∴CD//BH,
∴∠CDB=∠DBH,
∴$\overset{\frown}{BC}$=$\overset{\frown}{DH}$,
∴DH=BC=2,
∴AH=$\sqrt{AD^{2}+DH^{2}}$=$\sqrt{6^{2}+2^{2}}$=$2\sqrt{10}$.故答案为$2\sqrt{10}$.
6 新考向 开放性试题 如图,$A,B是\odot O$上的点, 且$∠AOB = 60^{\circ}$, 在这个图中, 仅用无刻度的直尺能画出的角的度数可以是____. (只要求写出四个)
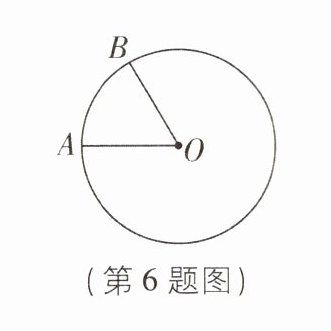

答案:
6.30°,60°,90°,120°(答案不唯一) 【解析】如图,连接 AB,过点 O 作射线 AD 交⊙O 于点 C,连接 BC.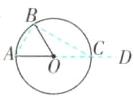
∵∠AOB=60°,OA=OB,
∴△AOB 是等边三角形,
∴∠OAB=∠OBA=∠AOB=60°,因此可以得到 60°的角
∵AC 是⊙O 的直径,
∴∠ABC=90°,因此可以得到 90°的角∠ACB=$\frac{1}{2}$∠AOB=30°,因此可以得到 30°的角∠BOC=180° - ∠AOB=120°,因此可以得到 120°的角∠BCD=180° - ∠ACB=150°,因此可以得到 150°的角,同时还可以画出 180°的角
6.30°,60°,90°,120°(答案不唯一) 【解析】如图,连接 AB,过点 O 作射线 AD 交⊙O 于点 C,连接 BC.

∵∠AOB=60°,OA=OB,
∴△AOB 是等边三角形,
∴∠OAB=∠OBA=∠AOB=60°,因此可以得到 60°的角
∵AC 是⊙O 的直径,
∴∠ABC=90°,因此可以得到 90°的角∠ACB=$\frac{1}{2}$∠AOB=30°,因此可以得到 30°的角∠BOC=180° - ∠AOB=120°,因此可以得到 120°的角∠BCD=180° - ∠ACB=150°,因此可以得到 150°的角,同时还可以画出 180°的角
7 [2024 江苏盐城亭湖区质检]如图,$AB是\odot O$的直径, 弦$CD⊥AB于点E$, 连接$AD,BD$.
(1) 求证:$∠ADC = ∠ABD$;
(2) 作$OF⊥AD于点F$, 若$\odot O的半径为10$,$OE = 6$, 求$OF$的长.
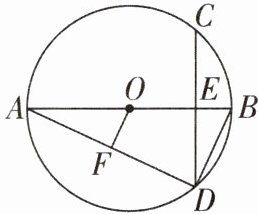
(1) 求证:$∠ADC = ∠ABD$;
(2) 作$OF⊥AD于点F$, 若$\odot O的半径为10$,$OE = 6$, 求$OF$的长.

答案:
7.
(1)【证明】
∵AB 是直径,
∴∠ADB=90°,
∴∠A + ∠ABD=90°.
∵CD⊥AB,
∴∠A + ∠ADC=90°,
∴∠ADC=∠ABD.
(2)【解】如图,连接 OD.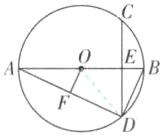
∵OA=OD=10,OE=6,
∴DE=8,AE=16,
∴在 Rt△ADE 中,AD=$\sqrt{16^{2}+8^{2}}$=$8\sqrt{5}$.
∵OF⊥AD,
∴AF=$\frac{1}{2}$AD=$4\sqrt{5}$,
∴OF=$\sqrt{10^{2}-(4\sqrt{5})^{2}}$=$2\sqrt{5}$.
7.
(1)【证明】
∵AB 是直径,
∴∠ADB=90°,
∴∠A + ∠ABD=90°.
∵CD⊥AB,
∴∠A + ∠ADC=90°,
∴∠ADC=∠ABD.
(2)【解】如图,连接 OD.

∵OA=OD=10,OE=6,
∴DE=8,AE=16,
∴在 Rt△ADE 中,AD=$\sqrt{16^{2}+8^{2}}$=$8\sqrt{5}$.
∵OF⊥AD,
∴AF=$\frac{1}{2}$AD=$4\sqrt{5}$,
∴OF=$\sqrt{10^{2}-(4\sqrt{5})^{2}}$=$2\sqrt{5}$.
如图是用$\odot O$制作的表盘模型, 其中点$A与B$分别与整钟点“$2$时”“$6$时”重合, 要使$∠ABC = 90^{\circ}$, 则点$C$应位于 (
A.“$7$时”处
B.“$8$时”处
C.“$9$时”处
D.“$10$时”处
B
)A.“$7$时”处
B.“$8$时”处
C.“$9$时”处
D.“$10$时”处
答案:
8.B 【解析】
∵∠ABC=90°,
∴AC 是⊙O 的直径,即∠AOC=180°.
∵点 A 与整钟点"2 时"重合,整钟点"2 时"与整钟点"8 时"相对,
∴点 C 应位于"8 时"处.故选 B.
∵∠ABC=90°,
∴AC 是⊙O 的直径,即∠AOC=180°.
∵点 A 与整钟点"2 时"重合,整钟点"2 时"与整钟点"8 时"相对,
∴点 C 应位于"8 时"处.故选 B.
9 如图, 点$A,B,C,D都在\odot O$上,$∠B = 90^{\circ}$,$AD = 3$,$CD = 2$, 则$\odot O$的直径的长是
$\sqrt{13}$
.
答案:
9.$\sqrt{13}$ 【解析】连接 AC.
∵∠B=90°,
∴AC 是⊙O 的直径,
∴∠ADC=90°.
∵AD=3,CD=2,
∴AC=$\sqrt{AD^{2}+CD^{2}}$=$\sqrt{13}$.故答案为$\sqrt{13}$.
∵∠B=90°,
∴AC 是⊙O 的直径,
∴∠ADC=90°.
∵AD=3,CD=2,
∴AC=$\sqrt{AD^{2}+CD^{2}}$=$\sqrt{13}$.故答案为$\sqrt{13}$.
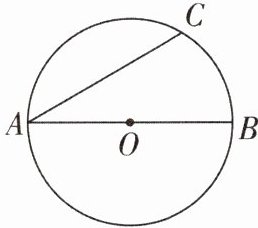
10 如图,$AB是圆O$的直径,$AC是圆O$的弦,$AB = 2$,$AC = \sqrt{3}$. 在图中画出弦$AD$, 使$AD = 1$, 则$∠CAD$的度数为____.

答案:
10.30°或 90° 【解析】如图,连接 CB,则∠ACB=90°.在 Rt△ABC 中,BC=$\sqrt{AB^{2}-AC^{2}}$=1,
∴BC=$\frac{1}{2}$AB,
∴∠OAC=30°.
①当 AD 与 AC 在直径 AB 的两旁时,连接 OD.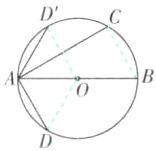
∵AB=2,AD=1,
∴AD=OD=OA,
∴△OAD 为等边三角形,
∴∠OAD=60°,
∴∠CAD=∠CAB + ∠OAD=30° + 60°=90°.②当 AD(D')与 AC 在直径 AB 的同旁时,则∠CAD'=∠OAD' - ∠CAB=60° - 30°=30°.综上,∠CAD=30°或 90°.
10.30°或 90° 【解析】如图,连接 CB,则∠ACB=90°.在 Rt△ABC 中,BC=$\sqrt{AB^{2}-AC^{2}}$=1,
∴BC=$\frac{1}{2}$AB,
∴∠OAC=30°.
①当 AD 与 AC 在直径 AB 的两旁时,连接 OD.

∵AB=2,AD=1,
∴AD=OD=OA,
∴△OAD 为等边三角形,
∴∠OAD=60°,
∴∠CAD=∠CAB + ∠OAD=30° + 60°=90°.②当 AD(D')与 AC 在直径 AB 的同旁时,则∠CAD'=∠OAD' - ∠CAB=60° - 30°=30°.综上,∠CAD=30°或 90°.
查看更多完整答案,请扫码查看


