第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
7. 方程思想 一根粗细不均匀的木棒AB在O点被悬挂起来,$AO= OC$.在A、C两点分别挂上不同数量的同种钩码后,木棒刚好在水平位置平衡,如图所示.若在木棒的A、C两点各减少两个钩码,则木棒AB( ).
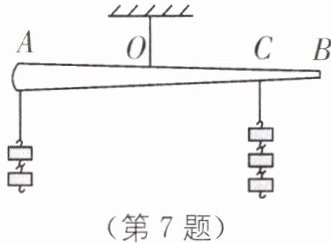
A.仍保持平衡
B.绕O点顺时针方向转动
C.绕O点逆时针方向转动
D.平衡被破坏,转动方向不定

A.仍保持平衡
B.绕O点顺时针方向转动
C.绕O点逆时针方向转动
D.平衡被破坏,转动方向不定
答案:
7.A [解析]由题知,AO=OC,A、C两点的力不同,说明木棒的重心不在O点,因为C点受到的力大于A点受到的力,所以木棒的重心在O点的左侧。设木棒的重心在D点,木棒所受重力为G₀,一个钩码重力为G,如答图所示,由题意,木棒原来平衡,则F左×AO+G₀×OD=F右×OC,2G×AO+G₀×OD=3G×OC,G₀×DO=G×OC,在木棒的A、C两点各减少两个钩码,左边力和力臂的乘积为G₀×OD,右边力和力臂的乘积为G×OC,由于G₀×OD=G×OC,所以木棒仍平衡。易错警示:通过杠杆平衡条件判断木棒的重心不在O点,而是在O点的左侧。
7.A [解析]由题知,AO=OC,A、C两点的力不同,说明木棒的重心不在O点,因为C点受到的力大于A点受到的力,所以木棒的重心在O点的左侧。设木棒的重心在D点,木棒所受重力为G₀,一个钩码重力为G,如答图所示,由题意,木棒原来平衡,则F左×AO+G₀×OD=F右×OC,2G×AO+G₀×OD=3G×OC,G₀×DO=G×OC,在木棒的A、C两点各减少两个钩码,左边力和力臂的乘积为G₀×OD,右边力和力臂的乘积为G×OC,由于G₀×OD=G×OC,所以木棒仍平衡。易错警示:通过杠杆平衡条件判断木棒的重心不在O点,而是在O点的左侧。

8. 如图甲所示,停车场的入口处常用横杆来控制车辆的出入.将横杆看作一个质量分布均匀的杠杆,如图乙所示,O为杠杆的支点,杠杆的重力$G= 50\ \text{N}$,$AB= 3\ \text{m}$,$AO= 0.3\ \text{m}$.下列说法正确的是(
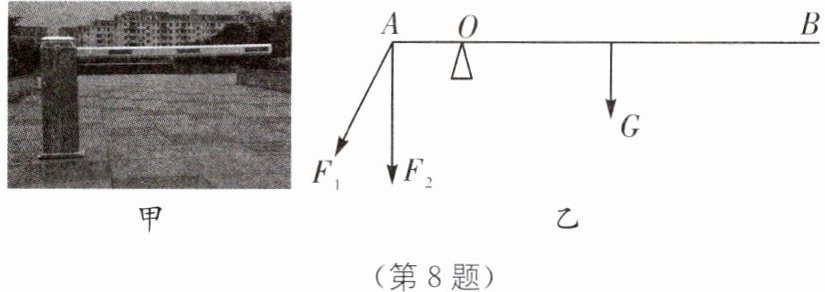
(第8题)
A.升起横杆时,施加在A端的力$F_{1}$为动力,此时横杆是省力杠杆
B.升起横杆时,沿$F_{1}方向比沿F_{2}$方向更省力
C.相同条件下,在A端施加的动力越靠近O点,升起横杆所需的动力越小
D.要使横杆AB保持水平平衡,则在A端施加的最小力为200 N
D
).
(第8题)
A.升起横杆时,施加在A端的力$F_{1}$为动力,此时横杆是省力杠杆
B.升起横杆时,沿$F_{1}方向比沿F_{2}$方向更省力
C.相同条件下,在A端施加的动力越靠近O点,升起横杆所需的动力越小
D.要使横杆AB保持水平平衡,则在A端施加的最小力为200 N
答案:
8.D [解析]升起横杆时,施加在A端的力为动力,此时的动力臂要小于阻力臂,为费力杠杆,故A错误;升起横杆时,沿F₁方向的动力臂比沿F₂方向的动力臂要小,根据杠杆的平衡条件可知,此时会更费力,故B错误;相同条件下,在A端施加的动力越靠近O点,动力臂越小,阻力和阻力臂不变,根据杠杆平衡条件可知,升起横杆所需的动力越大,故C错误;要使横杆AB保持水平平衡且施加的力最小,是应沿力F₂方向,根据杠杆的平衡条件可知F×OA=G×(AB/2 - OA),即F×0.3m = 50N×(3/2m - 0.3m),解得F = 200N,即在A端施加的最小的力为200N,故D正确。
9. 跨学科 数形结合 如图所示为吸盘式挂杆,将吸盘压在瓷砖上排尽其中的空气,挂杆就能被固定在瓷砖上,挂有平底锅的挂钩沿光滑水平横杆从P点开始向吸盘B移动.若吸盘与横杆的重力、吸盘大小均忽略不计,设挂钩与吸盘A的距离为l,则吸盘A受到的摩擦力F的大小与l的关系图像为(
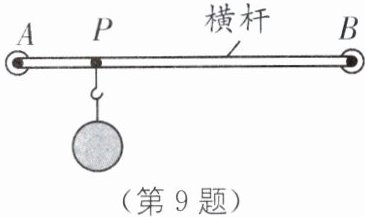

D
).

答案:
9.D [解析]以吸盘B为支点,挂钩的滑环与吸盘B的距离PB为动力臂,AB为阻力臂,挂钩对横杆的拉力为动力,其大小等于平底锅的重力,用G表示,吸盘A受到的摩擦力F为阻力,根据杠杆的平衡条件可得G×PB = F×AB,则F = (G×PB)/AB = (G×(AB - l))/AB = G - (G/AB)×l,因为AB、G不变,所以该函数关系式为一次函数,根据函数的性质可知吸盘A受到的摩擦力F的大小随l的增大而减小,又因为l > 0,且当l = AB时F = 0,故D符合题意。
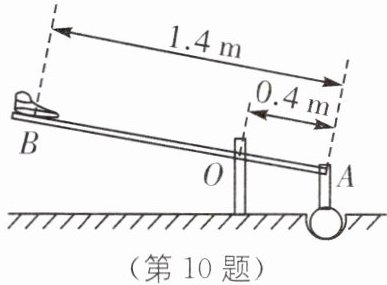
10. 新情境 舂米工具 如图所示是农村舂米工具的结构示意图.O为固定转轴,A处连接着石球,石球重力为50 N,不计摩擦和杆重.
(1)脚沿垂直于杆的方向用力$F_{1}$缓慢将石球抬起,$F_{1}$的力臂为______m,此时舂米工具是一个______(填“省”或“费”)距离的杠杆.
(2)脚沿竖直向下的方向用力$F_{2}$缓慢将石球抬起,则$F_{2}$______(填“>”“=”或“<”)$F_{1}$.石球被缓慢抬起的过程中,$F_{2}$的大小______(填“变大”“不变”或“变小”).
(1)脚沿垂直于杆的方向用力$F_{1}$缓慢将石球抬起,$F_{1}$的力臂为______m,此时舂米工具是一个______(填“省”或“费”)距离的杠杆.
(2)脚沿竖直向下的方向用力$F_{2}$缓慢将石球抬起,则$F_{2}$______(填“>”“=”或“<”)$F_{1}$.石球被缓慢抬起的过程中,$F_{2}$的大小______(填“变大”“不变”或“变小”).

答案:
10.
(1)1.0 费
(2)> 不变 [解析]
(1)不计摩擦和杆重,如答图所示,O为支点,脚沿与杆垂直的方向用力F₁时,其力臂为OB,OB = 1.4m - 0.4m = 1.0m,阻力臂为OD,OB > OD,由杠杆平衡条件可得F₁·OB = G·OD,此杠杆为省力杠杆,即杠杆属于费距离杠杆。
(2)当脚沿竖直向下用力时,动力臂为OC,阻力臂为OD,脚沿竖直向下用力时的动力臂OC小于脚沿与杆垂直方向用力时的动力臂OB,故F₂ > F₁;石球被缓慢抬起的过程中,由几何知识可知,F₂的力臂与G的力臂比值保持不变,所以F₂的大小也不变。
10.
(1)1.0 费
(2)> 不变 [解析]
(1)不计摩擦和杆重,如答图所示,O为支点,脚沿与杆垂直的方向用力F₁时,其力臂为OB,OB = 1.4m - 0.4m = 1.0m,阻力臂为OD,OB > OD,由杠杆平衡条件可得F₁·OB = G·OD,此杠杆为省力杠杆,即杠杆属于费距离杠杆。
(2)当脚沿竖直向下用力时,动力臂为OC,阻力臂为OD,脚沿竖直向下用力时的动力臂OC小于脚沿与杆垂直方向用力时的动力臂OB,故F₂ > F₁;石球被缓慢抬起的过程中,由几何知识可知,F₂的力臂与G的力臂比值保持不变,所以F₂的大小也不变。

11. 某学校在操场上举办秋季运动会的开幕式.入场时,小明竖直举着九(2)班的班牌走在最前列,如图所示.匀速前进时,班牌受到水平向后的风的阻力为10 N,作用在A点.若将班牌视为杠杆,AC间的距离是BC间距离的3倍.他将图中B点作为支点,手对另一点施加的力为
20
N,这个力的方向是水平向后
(填“向前”或“向后”).若他将图中C点作为支点,手对另一点施加的力为30
N.
答案:
11.20 向后 30 [解析]AC间的距离是BC间距离的3倍,即l_AC:l_BC = 3:1,所以l_AB:l_BC = 2:1,若以B点作为支点,A点受到向后的力为阻力F₂,AB为阻力臂l_AB,A、C两点位于支点的两侧,要使杠杆平衡,则C点受到的力为动力F₁,方向向后,BC为动力臂l_BC,根据杠杆的平衡条件得,手对C点施加的力为F₁ = (l_AB/l_BC)F₂ = 2/1×10N = 20N。若以C点作为支点,A点受到向后的力为阻力F₂,AC为阻力臂l_AC,B点受到的力为动力F₁',BC为动力臂l_BC,根据杠杆的平衡条件得,手对B点施加的力为F₁' = (l_AC/l_BC)F₂ = 3/1×10N = 30N。
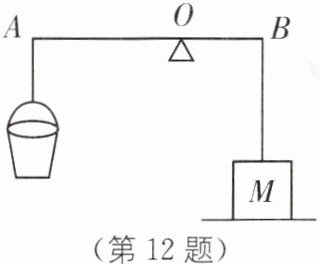
12. (2023·广东江门月考)在轻质杠杆AB的A端悬挂一个质量为2 kg的空桶,$AO:OB= 2:1$.将质量分布均匀、重为240 N的正方体工件M通过细线与B端相连,如图所示.此时杠杆在水平位置平衡,且M对地面的压强为5000 Pa,不计摩擦(g取10 N/kg),求:
(1)此时细线对M的拉力;
(2)工件M的密度;
(3)若将M沿竖直方向截去部分,并将截取的部分放入空桶中,使M对地面的压强变为原来的五分之三,求截去部分的质量.
(1)此时细线对M的拉力;
(2)工件M的密度;
(3)若将M沿竖直方向截去部分,并将截取的部分放入空桶中,使M对地面的压强变为原来的五分之三,求截去部分的质量.

答案:
12.
(1)40N
(2)3×10³kg/m³
(3)3.2kg[解析]
(1)A端拉力为F_A = G_A = m_A g = 2kg×10N/kg = 20N,由杠杆平衡原理可知OA×F_A = OB×F_B,细线对M的拉力为F_B = (OA/OB)×G_A = 2/1×20N = 40N。
(2)地面对M的支持力为F_支 = G_M - F_B = 240N - 40N = 200N,M对地面的压力与地面对M的支持力是一对相互作用力,大小相等,所以M对地面的压力为F_压 = F_支 = 200N,M对地面的压强为5000Pa,则M的底面积S = F_压/p = 200N/5000Pa = 0.04m²,则正方体工件M的棱长l = 0.2m,整个正方体工件M的体积为V = (0.2m)³ = 8×10⁻³m³,由G = mg可知M的质量m_M = G_M/g = 240N/10N/kg = 24kg,工件M的密度为ρ = m_M/V = 24kg/8×10⁻³m³ = 3×10³kg/m³。
(3)设工件M截去部分的质量为m,则截去部分的体积为V_切 = m/ρ,则切去部分的底面积为S_切 = V_切/l = (m/ρ)/l = m/(ρl),则工件M切去一部分后与地面的接触面积为S' = S - S_切 = S - m/(ρl),由题意可知,切割后M对地面的压强p' = 3/5 p = 3/5×5000Pa = 3000Pa,此时M对地面的压力F = p'S' = p'(S - m/(ρl)),压力和支持力是一对相互作用力,大小相等,此时的支持力为F_支' = F = p'(S - m/(ρl))…①,此时B端绳子的拉力为F_B' = G_M - mg - F_支'…②,由杠杆平衡原理可知OA×(G_A + mg) = OB×F_B',解得F_B' = (OA/OB)×(G_A + mg) = 2(G_A + mg)…③,由①②③解得m = (G_M - 2G_A - p'S)/(3g - p'/ρl) = (240N - 2×20N - 3000Pa×0.04m²)/(3×10N/kg - 3000Pa/(3×10³kg/m³×0.2m)) = 3.2kg。
(1)40N
(2)3×10³kg/m³
(3)3.2kg[解析]
(1)A端拉力为F_A = G_A = m_A g = 2kg×10N/kg = 20N,由杠杆平衡原理可知OA×F_A = OB×F_B,细线对M的拉力为F_B = (OA/OB)×G_A = 2/1×20N = 40N。
(2)地面对M的支持力为F_支 = G_M - F_B = 240N - 40N = 200N,M对地面的压力与地面对M的支持力是一对相互作用力,大小相等,所以M对地面的压力为F_压 = F_支 = 200N,M对地面的压强为5000Pa,则M的底面积S = F_压/p = 200N/5000Pa = 0.04m²,则正方体工件M的棱长l = 0.2m,整个正方体工件M的体积为V = (0.2m)³ = 8×10⁻³m³,由G = mg可知M的质量m_M = G_M/g = 240N/10N/kg = 24kg,工件M的密度为ρ = m_M/V = 24kg/8×10⁻³m³ = 3×10³kg/m³。
(3)设工件M截去部分的质量为m,则截去部分的体积为V_切 = m/ρ,则切去部分的底面积为S_切 = V_切/l = (m/ρ)/l = m/(ρl),则工件M切去一部分后与地面的接触面积为S' = S - S_切 = S - m/(ρl),由题意可知,切割后M对地面的压强p' = 3/5 p = 3/5×5000Pa = 3000Pa,此时M对地面的压力F = p'S' = p'(S - m/(ρl)),压力和支持力是一对相互作用力,大小相等,此时的支持力为F_支' = F = p'(S - m/(ρl))…①,此时B端绳子的拉力为F_B' = G_M - mg - F_支'…②,由杠杆平衡原理可知OA×(G_A + mg) = OB×F_B',解得F_B' = (OA/OB)×(G_A + mg) = 2(G_A + mg)…③,由①②③解得m = (G_M - 2G_A - p'S)/(3g - p'/ρl) = (240N - 2×20N - 3000Pa×0.04m²)/(3×10N/kg - 3000Pa/(3×10³kg/m³×0.2m)) = 3.2kg。
查看更多完整答案,请扫码查看


