第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
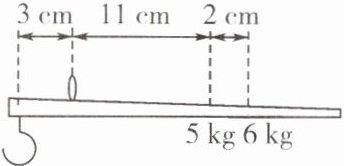
【例】(上海市第三十二届初中物理竞赛初赛)小明为课题研究小组提供了一把家中的旧杆秤(秤砣遗失),杆秤的刻度大多数模糊不清,只有5 kg和6 kg的刻度清晰可辨。小组成员对杆秤的外形进行了测量,测量结果如图所示。课题研究小组对杆秤的重心(不包括秤砣)和秤砣质量的判断正确的是(
A.杆秤重心在杆秤提纽的右侧,秤砣的质量为2.0 kg
B.杆秤重心在杆秤提纽的右侧,秤砣的质量为1.5 kg
C.杆秤重心在杆秤提纽的左侧,秤砣的质量为1.5 kg
D.杆秤重心在杆秤提纽的左侧,秤砣的质量为2.0 kg
解析:由图可以知道,5 kg到6 kg质量增加了1 kg,而杠杆的长增加了2 cm,杆秤上的刻度是均匀的,所以,从0刻度线到5 kg的位置,杠杆的长应该为10 cm,即0刻度线在提纽的右侧,所以该杆秤的重心应该在提纽的左侧(因为0刻度线处要挂秤砣才能使杠杆在水平位置平衡)。设杆秤的重心到提纽的距离为s,秤砣的质量为m,杆秤的质量为$m_{杆}$,由杠杆的平衡条件$F_{1}l_{1}= F_{2}l_{2}$可知,$5\ \text{kg}× g× 3\ \text{cm}+m_{杆}gs= mg× 11\ \text{cm}$,化简为$5\ \text{kg}× 3\ \text{cm}+m_{杆}s= m× 11\ \text{cm}…①$,$6\ \text{kg}× g× 3\ \text{cm}+m_{杆}gs= mg× (11\ \text{cm}+2\ \text{cm})$,化简为$6\ \text{kg}× 3\ \text{cm}+m_{杆}s= m× (11\ \text{cm}+2\ \text{cm})…②$,联立①②可得$m= 1.5\ \text{kg}$。
答案:C
C
)。
A.杆秤重心在杆秤提纽的右侧,秤砣的质量为2.0 kg
B.杆秤重心在杆秤提纽的右侧,秤砣的质量为1.5 kg
C.杆秤重心在杆秤提纽的左侧,秤砣的质量为1.5 kg
D.杆秤重心在杆秤提纽的左侧,秤砣的质量为2.0 kg
解析:由图可以知道,5 kg到6 kg质量增加了1 kg,而杠杆的长增加了2 cm,杆秤上的刻度是均匀的,所以,从0刻度线到5 kg的位置,杠杆的长应该为10 cm,即0刻度线在提纽的右侧,所以该杆秤的重心应该在提纽的左侧(因为0刻度线处要挂秤砣才能使杠杆在水平位置平衡)。设杆秤的重心到提纽的距离为s,秤砣的质量为m,杆秤的质量为$m_{杆}$,由杠杆的平衡条件$F_{1}l_{1}= F_{2}l_{2}$可知,$5\ \text{kg}× g× 3\ \text{cm}+m_{杆}gs= mg× 11\ \text{cm}$,化简为$5\ \text{kg}× 3\ \text{cm}+m_{杆}s= m× 11\ \text{cm}…①$,$6\ \text{kg}× g× 3\ \text{cm}+m_{杆}gs= mg× (11\ \text{cm}+2\ \text{cm})$,化简为$6\ \text{kg}× 3\ \text{cm}+m_{杆}s= m× (11\ \text{cm}+2\ \text{cm})…②$,联立①②可得$m= 1.5\ \text{kg}$。
答案:C
答案:
解:由图可知,5kg到6kg刻度间距为2cm,质量增加1kg,刻度均匀,故0刻度线到5kg刻度线距离为5×2cm=10cm,0刻度线在提纽右侧,因此杆秤重心在提纽左侧。
设杆秤重心到提纽距离为s,秤砣质量为m,杆秤质量为$m_{杆}$。
根据杠杆平衡条件:
当称5kg物体时:$5\ \text{kg}×g×3\ \text{cm}+m_{杆}gs=mg×11\ \text{cm}$,化简得$5×3 + m_{杆}s = 11m$…①
当称6kg物体时:$6\ \text{kg}×g×3\ \text{cm}+m_{杆}gs=mg×(11+2)\ \text{cm}$,化简得$6×3 + m_{杆}s = 13m$…②
②-①得:$18 - 15 = 13m - 11m$,即$3 = 2m$,解得$m=1.5\ \text{kg}$。
答案:C
设杆秤重心到提纽距离为s,秤砣质量为m,杆秤质量为$m_{杆}$。
根据杠杆平衡条件:
当称5kg物体时:$5\ \text{kg}×g×3\ \text{cm}+m_{杆}gs=mg×11\ \text{cm}$,化简得$5×3 + m_{杆}s = 11m$…①
当称6kg物体时:$6\ \text{kg}×g×3\ \text{cm}+m_{杆}gs=mg×(11+2)\ \text{cm}$,化简得$6×3 + m_{杆}s = 13m$…②
②-①得:$18 - 15 = 13m - 11m$,即$3 = 2m$,解得$m=1.5\ \text{kg}$。
答案:C
1.(第二十五届全国初中应用物理竞赛)如图所示是一种案秤的照片。根据这张照片估计,如果将该案秤配备的标有“1 kg”字样的槽码放在秤盘上,那么测得其质量应约为(

A.1 kg
B.0.2 kg
C.0.1 kg
D.0.5 kg
B
)。
A.1 kg
B.0.2 kg
C.0.1 kg
D.0.5 kg
答案:
1.B [解析]槽码标有1 kg的字样,说明将其放在槽码盘上时,在秤盘中放置1 kg的物体恰好使杠杆平衡,设槽码的实际质量为$m_{码}$,其对应的力臂为$l_{码}$,物体所对应的力臂为$l_{物}$,根据杠杆平衡条件得$m_{码}gl_{码}=m_{物}gl_{物}$,由图可知,$m_{码}=\frac {m_{物}l_{物}}{l_{码}}\approx \frac {1}{5}m_{物}=\frac {1}{5}×1kg=0.2kg.$
2.(多选)(上海市第三十二届初中物理竞赛初赛)如图所示,工人用动滑轮匀速提升重物。重物的重力为$G_{1}$,动滑轮的重力为$G_{2}$,装置的机械效率为η,不计绳子重力和一切摩擦,则拉力F为(
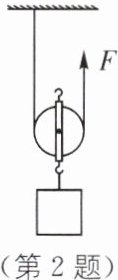
A.$\frac{G_{1}+G_{2}}{2}$
B.$\frac{G_{1}}{2\eta}$
C.$\frac{G_{1}+\eta G_{2}}{\eta}$
D.$\frac{G_{2}}{2(1-\eta)}$
A、B、D
)。
A.$\frac{G_{1}+G_{2}}{2}$
B.$\frac{G_{1}}{2\eta}$
C.$\frac{G_{1}+\eta G_{2}}{\eta}$
D.$\frac{G_{2}}{2(1-\eta)}$
答案:
2.A、B、D [解析]因为不计绳重和摩擦,所以$F=\frac {G_{1}+G_{2}}{2}.$使用动滑轮提升重物时,克服重物的重力做的功为有用功,即$W_{有用}=G_{1}h$;绳子自由端的拉力做的功为总功,即$W_{总}=F×2h$;根据机械效率公式$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {G_{1}h}{F×2h}×100\% =\frac {G_{1}}{2F}×100\% $,可得$F=\frac {G_{1}}{2η}$.对动滑轮做的功为额外功,那么额外功和总功的比为$1-η=\frac {G_{2}h}{F×2h}=\frac {G_{2}}{2F}$,可得$F=\frac {G_{2}}{2(1-η)}.$
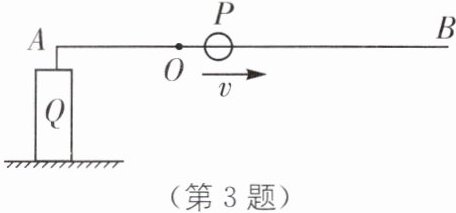
3.(青岛市西海岸新区竞赛)如图所示,水平光滑轻质硬直杆AB可绕固定轴O点转动,$OA= 2\ \text{m}$,OB足够长,杆左端A点用轻绳系一重量为100 N圆柱体Q,圆柱体Q的底面积为$20\ \text{cm}^{2}$,静置于水平地面上。直杆O点右侧穿有重量为50 N的铁环P,现让铁环P以$0.2\ \text{m/s}$的速度,从O点开始向B端匀速运动。
(1)求4 s末圆柱体Q对地面的压强。
(2)为不使硬杆转动,铁环P从O点开始向右运动的最长时间。
(3)试推导铁环P从O点开始运动,直到硬杆AB开始转动,这一过程中,圆柱体Q对地面的压强随时间变化的数学关系式,并画出两者(p-t)关系图像,并标记出图线与坐标轴交点数值。
(1)求4 s末圆柱体Q对地面的压强。
(2)为不使硬杆转动,铁环P从O点开始向右运动的最长时间。
(3)试推导铁环P从O点开始运动,直到硬杆AB开始转动,这一过程中,圆柱体Q对地面的压强随时间变化的数学关系式,并画出两者(p-t)关系图像,并标记出图线与坐标轴交点数值。

答案:
3.
(1)$4×10^{4}Pa$
(2)20 s
(3)见解析
[解析]
(1)由$v=\frac {s}{t}$可得,在4 s内铁环P移动的距离$s_{1}=vt_{1}=0.2m/s×4s=0.8m$,即4 s末铁环重力的力臂$OP_{1}=s_{1}=0.8m$,由杠杆的平衡条件可得$F_{A1}×OA=G_{P}×OP_{1}$,则A端轻绳的拉力$F_{A1}=\frac {OP_{1}}{OA}G_{P}=\frac {0.8m}{2m}×50N=20N$,4 s末圆柱体Q对地面的压力$F_{1}=G_{Q}-F_{A1}=100N-20N=80N$,圆柱体Q对地面的压强$p_{1}=\frac {F_{1}}{S}=\frac {80N}{20×10^{-4}m^{2}}=4×10^{4}Pa.$
(2)硬杆恰好不转动时,A端细绳的拉力$F_{A2}=G_{Q}=100N$,由杠杆的平衡条件可得$F_{A2}×OA=G_{P}×OP_{2}$,此时铁环重力的力臂$OP_{2}=\frac {F_{A2}}{G_{P}}OA=\frac {100N}{50N}×2m=4m$,即铁环运动的距离$s_{2}=OP_{2}=4m$,则铁环P从O点开始向右运动的最长时间$t_{2}=\frac {s_{2}}{v}=\frac {4m}{0.2m/s}=20s.$
(3)当铁环运动的时间为t时,铁环重力的力臂$OP=s=vt=0.2m/s×t$,由杠杆的平衡条件可得,$F_{A}×OA=G_{P}×OP$,则A端轻绳的拉力$F_{A}=\frac {OP}{OA}G_{P}=\frac {0.2m/s×t}{2m}×50N=5t\cdot \frac {N}{s}$,圆柱体Q对地面的压力$F=G_{Q}-F_{A}=100N-5t\cdot \frac {N}{s}$,圆柱体Q对地面的压强$p=\frac {F}{S}=\frac {100N-5t\cdot \frac {N}{s}}{20×10^{-4}m^{2}}=5×10^{4}Pa-2.5×10^{3}t\cdot \frac {Pa}{s}$,根据表达式可知,p与t成一次函数关系,当$t=0s$时,$p_{0}=5×10^{4}Pa$,由
(2)可知,$t=20s$时,圆柱体对地面没有压力,即此时圆柱体对地面的压强为0;根据这两个特殊点和p与t成一次函数关系,作图如下:

3.
(1)$4×10^{4}Pa$
(2)20 s
(3)见解析
[解析]
(1)由$v=\frac {s}{t}$可得,在4 s内铁环P移动的距离$s_{1}=vt_{1}=0.2m/s×4s=0.8m$,即4 s末铁环重力的力臂$OP_{1}=s_{1}=0.8m$,由杠杆的平衡条件可得$F_{A1}×OA=G_{P}×OP_{1}$,则A端轻绳的拉力$F_{A1}=\frac {OP_{1}}{OA}G_{P}=\frac {0.8m}{2m}×50N=20N$,4 s末圆柱体Q对地面的压力$F_{1}=G_{Q}-F_{A1}=100N-20N=80N$,圆柱体Q对地面的压强$p_{1}=\frac {F_{1}}{S}=\frac {80N}{20×10^{-4}m^{2}}=4×10^{4}Pa.$
(2)硬杆恰好不转动时,A端细绳的拉力$F_{A2}=G_{Q}=100N$,由杠杆的平衡条件可得$F_{A2}×OA=G_{P}×OP_{2}$,此时铁环重力的力臂$OP_{2}=\frac {F_{A2}}{G_{P}}OA=\frac {100N}{50N}×2m=4m$,即铁环运动的距离$s_{2}=OP_{2}=4m$,则铁环P从O点开始向右运动的最长时间$t_{2}=\frac {s_{2}}{v}=\frac {4m}{0.2m/s}=20s.$
(3)当铁环运动的时间为t时,铁环重力的力臂$OP=s=vt=0.2m/s×t$,由杠杆的平衡条件可得,$F_{A}×OA=G_{P}×OP$,则A端轻绳的拉力$F_{A}=\frac {OP}{OA}G_{P}=\frac {0.2m/s×t}{2m}×50N=5t\cdot \frac {N}{s}$,圆柱体Q对地面的压力$F=G_{Q}-F_{A}=100N-5t\cdot \frac {N}{s}$,圆柱体Q对地面的压强$p=\frac {F}{S}=\frac {100N-5t\cdot \frac {N}{s}}{20×10^{-4}m^{2}}=5×10^{4}Pa-2.5×10^{3}t\cdot \frac {Pa}{s}$,根据表达式可知,p与t成一次函数关系,当$t=0s$时,$p_{0}=5×10^{4}Pa$,由
(2)可知,$t=20s$时,圆柱体对地面没有压力,即此时圆柱体对地面的压强为0;根据这两个特殊点和p与t成一次函数关系,作图如下:

查看更多完整答案,请扫码查看


