《2025年实验班提优训练九年级物理上册苏科版》

11. 如图所示,一根均匀的细木棒 OC,$OA= \frac {1}{4}OC$,B 为 OC 的中点.在 C 点施力将挂在 A 点的重为 180 N 的物体匀速提升 0.2 m,木棒的机械效率为 90%,这里的木棒是一种简单机械,称为杠杆,提升该物体做的有用功为36J,木棒重为10N(不计摩擦).

答案： 杠杆 36 10 [解析]由题图可知,木棒OC在力的作用下可绕固定点O转动,所以是杠杆;将物体匀速提升0.2m时,做的有用功$W_{有用}=Gh=180\ \text{N}× 0.2\ \text{m}=36\ \text{J}$.木棒的重心B上升的高度$h_{0}=0.4\ \text{m}$,克服木棒重力做的功为额外功,$W_{额外}=W_{总}-W_{有用}=$$\frac{W_{有用}}{\eta}$$-W_{有用}=$$\frac{36\ \text{J}}{90\%}$$-36\ \text{J}=$$\frac{36\ \text{J}}{0.9}$$-36\ \text{J}=4\ \text{J}$,所以木棒重$G_{0}=$$\frac{W_{额外}}{h_{0}}$$=$$\frac{4\ \text{J}}{0.4\ \text{m}}$$=10\ \text{N}$.

(1)在第 2 次实验中,滑轮组的机械效率$\eta $为88.9%.(结果保留一位小数)
(2)分析数据可得结论：同一滑轮组,提升的物体越重,滑轮组的机械效率越高(填“高”或“低”).
(3)根据实验结论推测,使用该滑轮组再次将重为 8 N 的物体匀速提升 10 cm,此时滑轮组的机械效率可能为C.
A. 71.6%
B. 82.6%
C. 92.4%
D. 100%
(4)另一实验小组改变动滑轮的重量,提升同一物体进行多次实验,获得数据并绘制出如图丁所示的图像.分析可知,被提升物体所受的重力相同时,动滑轮越重,滑轮组的机械效率越低(填“高”或“低”)；分析图像中的 A 点可知,被提升物体所受的重力为12N(忽略绳重和摩擦).

答案：
(1)88.9%
(2)高
(3)C
(4)低 12 [解析]
(1)由表格数据可知,在第2次实验中,钩码重$G_{物}=4\ \text{N}$,钩码上升的距离$h=10\ \text{cm}=0.1\ \text{m}$,绳自由端的拉力$F=1.5\ \text{N}$,绳自由端移动的距离$s_{绳}=30\ \text{cm}=$$0.3\ \text{m}$,则滑轮组的机械效率$\eta=$$\frac{W_{有用}}{W_{总}}$$× 100\%=$$\frac{G_{物}h}{Fs_{绳}}$$× 100\%=$$\frac{4\ \text{N}× 0.1\ \text{m}}{1.5\ \text{N}× 0.3\ \text{m}}$$× 100\%\approx 88.9\%$.
(2)由表中数据可知,第1次实验中,$G_{物}=2\ \text{N}$,$\eta=83.3\%$,第2次实验中,$G_{物}=4\ \text{N}$,$\eta=88.9\%$,第3次实验中,$G_{物}=6\ \text{N}$,$\eta=$$90.9\%$,所以可得结论:同一滑轮组,提升的物体越重,滑轮组的机械效率越高.
(3)当物重$G_{物}=8\ \text{N}\gt 6\ \text{N}$时,由
(2)中结论可知,滑轮组的机械效率$\eta\gt 90.9\%$,又因滑轮组的机械效率不可能达到100%,所以,此时滑轮组的机械效率可能为92.4%,故C符合题意.
(4)由图丁可知,当提升同一物体时,动滑轮越重,滑轮组的机械效率越低.图像中A点对应的数据为动滑轮重$G_{动}=4\ \text{N}$,此时滑轮组的机械效率$\eta=75\%$,不计绳重与摩擦时,滑轮组的机械效率$\eta=$$\frac{W_{有用}}{W_{总}}$$× 100\%=$$\frac{W_{有用}}{W_{有用}+W_{额外}}$$× 100\%=$$\frac{G_{物}h}{G_{物}h+G_{动}h}$$× 100\%=$$\frac{G_{物}}{G_{物}+G_{动}}$$× 100\%=$$\frac{G_{物}}{G_{物}+4\ \text{N}}$$× 100\%=75\%$,解得$G_{物}=12\ \text{N}$,所以被提升物体所受的重力为12N.

13. 同学们在学校的花园里散步时,看到校工师傅在用剪刀修剪树枝,发现他在修剪较粗硬的树枝时,需要把树枝夹在离剪刀轴很近的地方,手放在离剪刀轴最远的末端就会很轻松地剪断粗树枝了,看到这里,同学们就讨论起来了：为什么这样使用就会很容易剪断树枝呢？于是大家对杠杆的特性进行了如下探究.

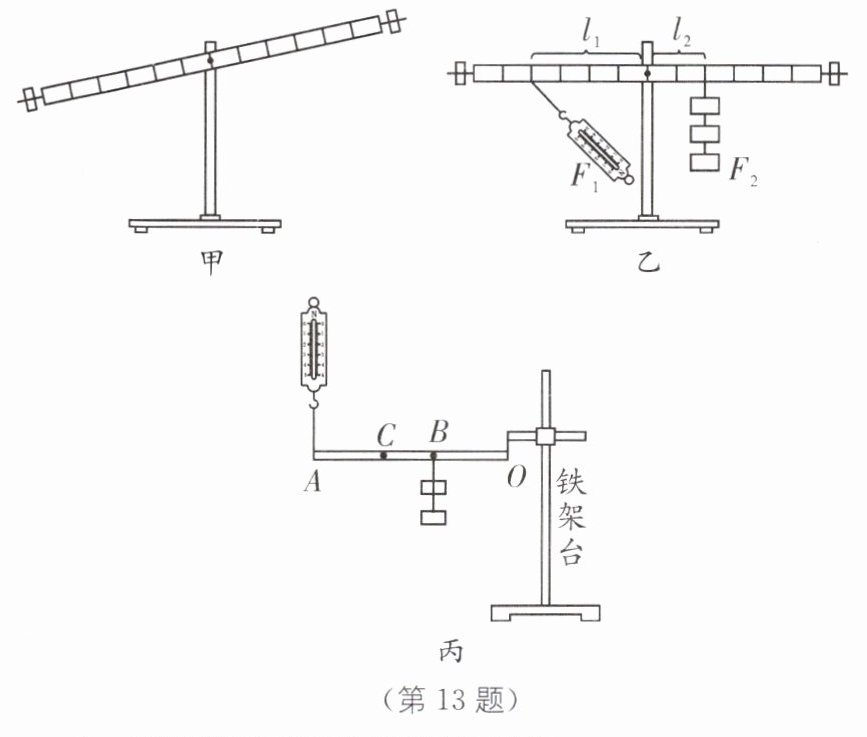
(一)“探究杠杆的平衡条件”
(1)当杠杆静止在如图甲所示的位置时,杠杆处于平衡状态；若此时杠杆左端下沉,应将右端的平衡螺母向右调节使杠杆在水平位置平衡,这样做的目的是消除杠杆重力对实验的影响.在实验时也需要让杠杆在水平位置平衡,其目的是便于测量力臂.
(2)小明同学用图乙所示的方法使杠杆处于平衡状态,测出此时的拉力大小为$F_{1}$,发现$F_{1}l_{1}≠F_{2}l_{2}$,其原因是拉力$F_{1}$的力臂不是$l_{1}$.
(二)“探究杠杆的机械效率”
如图丙所示装置,每个钩码的质量为 m,O 为支点(支点处摩擦忽略不计).
(3)小明将 2 个钩码挂在 B 点,在 A 点竖直向上缓慢拉动弹簧测力计,拉力为 F,测得 A、B 两点上升的高度分别为 s、h,则此次杠杆的机械效率为$\eta _{1}= $$\frac{2mgh}{Fs}× 100\%$(用所测物理量的符号表示,g 值用符号 g 表示).
(4)取下挂在 B 点的钩码后,他又将 2 个钩码悬挂在 C 点,在 A 点竖直向上缓慢拉动弹簧测力计,使 C 点上升的高度也为 h,则弹簧测力计的示数将大于F,此次拉力做的总功将小于第一次做的总功,此次的机械效率$\eta _{2}$大于第一次的机械效率$\eta _{1}$.

答案：
(1)平衡 右 消除杠杆重力对实验的影响 便于测量力臂
(2)拉力$F_{1}$的力臂不是$l_{1}$
(3)$\frac{2mgh}{Fs}$$× 100\%$
(4)大于 小于 大于 [解析]
(1)若图甲中杠杆处于静止状态,说明杠杆受力平衡,处于平衡状态;若图甲中杠杆左侧下沉,说明左侧偏重,应将右端的平衡螺母向右调,直至杠杆水平平衡,可以消除杠杆重力对杠杆平衡的影响;在实验时也需要让杠杆在水平位置平衡,方便直接从杠杆上读出力臂大小.
(2)由图乙可知力$F_{1}$与$l_{1}$不垂直,说明$l_{1}$不是$F_{1}$的力臂,即力臂测量错误,所以得到$F_{1}l_{1}\neq F_{2}l_{2}$的结果.
(3)杠杆的机械效率$\eta_{1}=$$\frac{W_{有用}}{W_{总}}$$× 100\%=$$\frac{2mgh}{Fs}$$× 100\%$.
(4)取下挂在B点的钩码后,将2个钩码悬挂在C点,钩码的力臂变大,钩码的重力不变,拉力仍作用在A点,拉力的力臂不变,由$F_{1}l_{1}=F_{2}l_{2}$可知,拉力将变大,即拉力将大于F.钩码上升高度不变,所以有用功不变,杠杆上升高度变小,克服杠杆重力所做的额外功减小,所以拉力做的总功减小.由$\eta=$$\frac{W_{有用}}{W_{总}}$$× 100\%$可知,有用功不变,总功减小,则机械效率变大,即$\eta_{2}\gt \eta_{1}$.