《2025年实验班提优训练九年级物理上册苏科版》

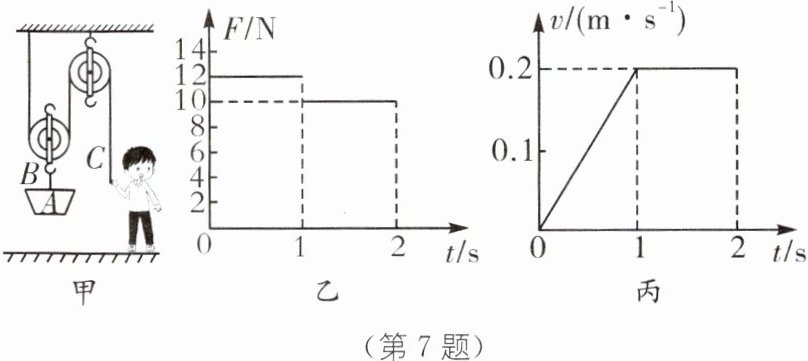
7. 如图甲所示的装置,A 是重为 10 N 的空吊篮,绳子 B 和 C 能承受的最大拉力分别为 100 N 和 60 N.质量为 50 kg 的小张同学将 A 提升到高处,施加的拉力 F 随时间变化关系如图乙所示,A 上升的速度 v 随时间变化关系如图丙所示.忽略绳重及摩擦,g 取 10 N/kg.下列结论正确的是( C ).
①动滑轮的重力为 9 N；②0~1 s 内拉力 F 做的功为 2.4 J；③1~2 s 内拉力 F 的功率为 4 W；④此装置提升重物的最大机械效率约为 81.8%.

A.①④
B.①③
C.②③④
D.③

答案： C [解析]由图丙可知,在1~2s内,A被匀速提升,由图乙可知拉力$F=10\ \text{N}$,由图甲知,$n=2$,忽略绳重及摩擦,拉力$F=$$\frac{1}{2}$$(G_{A}+G_{动})$,则动滑轮重力$G_{动}=2F-G_{A}=$$2× 10\ \text{N}-10\ \text{N}=10\ \text{N}$,故①错误;由图丙可知,0~1s内物体上升的距离$h=$$\frac{1}{2}$$× 0.2\ \text{m/s}× 1\ \text{s}=0.1\ \text{m}$,则自由端移动的距离$s=2h=2× 0.1\ \text{m}=0.2\ \text{m}$,由图乙可知,0~1s内拉力$F=12\ \text{N}$,则0~1s内拉力F做的功$W=Fs=$$12\ \text{N}× 0.2\ \text{m}=2.4\ \text{J}$,故②正确;由图丙可知,1~2s内A上升的速度$v_{A}=0.2\ \text{m/s}$,拉力端移动速度$v=2v_{A}=$$2× 0.2\ \text{m/s}=0.4\ \text{m/s}$,拉力F的功率$P=Fv=10\ \text{N}×$$0.4\ \text{m/s}=4\ \text{W}$,故③正确;设A被匀速提升,忽略绳重及摩擦,C处绳子拉力$F_{C}=$$\frac{1}{2}$$(F_{B}+G_{动})=$$\frac{1}{2}$$(F_{B}+10\ \text{N})$,则当C处最大拉力为60N时,B处拉力为110N,当B处最大拉力为100N时,C处拉力为55N,所以以B处最大拉力为准,B处的拉力$F_{B}=G_{A}+G=100\ \text{N}$,此装置最多能匀速运载货物的重力$G=F_{B}-G_{A}=100\ \text{N}-10\ \text{N}=$$90\ \text{N}$,此装置提升重物的机械效率随提升物重的增大而增大,此装置提升重物的最大机械效率$\eta=$$\frac{W_{有用}}{W_{总}}$$× 100\%=$$\frac{Gh}{F_{C最大}s}$$× 100\%=$$\frac{Gh}{F_{C最大}× 2h}$$× 100\%=$$\frac{G}{2F_{C最大}}$$× 100\%=$$\frac{90\ \text{N}}{2× 55\ \text{N}}$$× 100\%\approx 81.8\%$,故④正确.
易错警示 要注意:提升重物的最大机械效率$\eta=$$\frac{W_{有用}}{W_{总}}$$× 100\%=$$\frac{Gh}{F_{C最大}s}$$× 100\%=$$\frac{Gh}{F_{C最大}× 2h}$$× 100\%=$$\frac{G}{2F_{C最大}}$$× 100\%$.

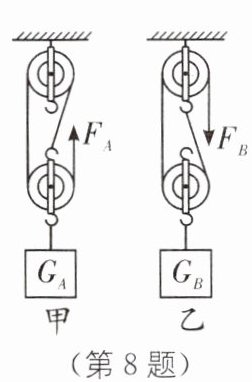
8. (2024·苏州工业园区五校期中)如图所示,用相同的滑轮安装成甲、乙两种装置,分别用拉力$F_{A}$、$F_{B}在相同时间内将重为G_{A}$、$G_{B}$的两个物体匀速提升相同高度,拉力的功率为$P_{A}$、$P_{B}$,绳子自由端移动的距离为$s_{A}$、$s_{B}$,不计绳重和摩擦,下列推理中正确的是(D).

A.若$G_{A}= G_{B}$,则$F_{A}= F_{B}$
B.若$G_{A}＞G_{B}$,则$s_{A}＞s_{B}$
C.若$F_{A}\lt F_{B}$,则$P_{A}\lt P_{B}$
D.若$F_{A}= F_{B}$,则$\eta _{甲}＞\eta _{乙}$

答案： D [解析]由图知,装置甲动滑轮上绳子的段数为3,装置乙动滑轮上绳子的段数为2,不计绳重和摩擦,由公式$nF=G_{物}+G_{动}$可知,$3F_{A}=G_{A}+G_{动}$,$2F_{B}=G_{B}+G_{动}$,若$G_{A}=G_{B}$,则$F_{A}\lt F_{B}$,故A错误;由图知,$s_{A}=3h$,$s_{B}=$$2h$,故$s_{A}\gt s_{B}$,$s_{A}$、$s_{B}$之间的关系与物体的重力大小无关,故B错误;相同时间内,$F_{A}$做的功为$W_{A}=F_{A}× 3h$,$F_{B}$做的功为$W_{B}=F_{B}× 2h$,仅根据$F_{A}\lt F_{B}$,不能推出$W_{A}$和$W_{B}$之间的关系,由$P=$$\frac{W}{t}$知,不能确定$P_{A}$、$P_{B}$的关系,故C错误;若$F_{A}=F_{B}$,则由$nF=G_{物}+G_{动}$可得,$G_{A}\gt$$G_{B}$,由$\eta=$$\frac{W_{有用}}{W_{总}}$$× 100\%=$$\frac{G_{物}h}{G_{物}h+G_{动}h}$$× 100\%=$$\frac{1}{1+\frac{G_{动}}{G_{物}}}$$× 100\%$可得,$G_{动}$相同时,$G_{物}$越大,$\eta$越大,则$\eta_{甲}\gt \eta_{乙}$,故D正确.故选D.

9. 用五个相同的滑轮和绳子组成如图所示的甲、乙两个滑轮组,分别将不同的物体$G_{1}和G_{2}$匀速提升相同高度,绳端所需的拉力 F 恰好相等,不计摩擦、绳和木板的重力.则绳端拉力 F 做的功之比为$W_{1}:W_{2}= $$1:2$,滑轮组的机械效率之比$\eta _{1}:\eta _{2}= $$1:1$.

答案： $1:2$ $1:1$ [解析]由图可知,$n_{甲}=2$,$n_{乙}=4$,将不同的物体$G_{1}$和$G_{2}$匀速提升相同高度,绳端所需的拉力F恰好相等,此时$s_{1}=2h$,$s_{2}=4h$,绳端拉力F做功之比为$W_{1}:W_{2}=Fs_{1}:Fs_{2}=s_{1}:s_{2}=2h:4h=1:2$;根据$F=$$\frac{1}{n}$$(G_{动}+G)$知,$G_{1}=2F-G_{动}$,$G_{2}=4F-2G_{动}$,根据$\eta=$$\frac{W_{有用}}{W_{总}}$$× 100\%=$$\frac{G}{nF}$$× 100\%$知,两滑轮组的机械效率之比为$\eta_{1}:\eta_{2}=$$\frac{G_{1}}{2F}$:$\frac{G_{2}}{4F}$=$$\frac{2F-G_{动}}{2F}$:$\frac{4F-2G_{动}}{4F}$=$$\frac{2F-G_{动}}{2F}$:$\frac{2× (2F-G_{动})}{2× 2F}$$=1:1$.

10. 《墨经·经下》里记载的一种斜面引重车,可以将重物拉举到所需的高度.如图所示为这种引重车的侧面示意图,该装置是一种省力(填“省力”或“费力”)机械.若用该引重车将重为 2000 N 的木箱从斜面的底端匀速拉到顶端用时 20 s.已知斜板长 2 m,高 0.8 m,此时后轮轴上绳子受到的拉力为 1000 N(不计绳重、轮与轴之间的摩擦),此过程中拉力的功率为100W,此装置的机械效率为80%.

答案： 省力 100 80% [解析]斜面在使用时可以省力,绳子上的拉力小于重物的重力,且车子后轮在该装置中是一个轮轴,人施加在车上的推力作用在轮上,绳子上的拉力作用在轴上,所以施加在车上的推力小于绳子上的拉力,所以该装置是一种省力机械.拉力做的总功$W_{总}=Fs=$$1000\ \text{N}× 2\ \text{m}=2000\ \text{J}$,拉力的功率为$P=$$\frac{W_{总}}{t}$$=$$\frac{2000\ \text{J}}{20\ \text{s}}$$=100\ \text{W}$,拉力做的有用功为$W_{有用}=Gh=$$2000\ \text{N}× 0.8\ \text{m}=1600\ \text{J}$,此装置的机械效率为$\eta=$$\frac{W_{有用}}{W_{总}}$$× 100\%=$$\frac{1600\ \text{J}}{2000\ \text{J}}$$× 100\%=80\%$.