第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
1. (2024·苏州姑苏区一模)如图甲所示,吊车正在对一辆交通事故车实施救援作业.该事故车总重为$1.2×10^4N,$吊车以0.5m/s的速度先将该车向上吊起3m,再水平向右移动6m后放到道路事故救援车上运回交警队.(g取10N/kg)
(1)吊车施救过程中对该车做了多少功?
(2)起重臂下滑轮组的结构如图乙所示,若钢丝绳上的拉力F为5000N,将该车向上吊起3m的过程中,拉力F的功率是多少?
(3)若不考虑钢丝绳重和摩擦,钢丝绳能承受的最大拉力是$3×10^4N,$该滑轮组能否吊起重为$8.8×10^4N$的物体?
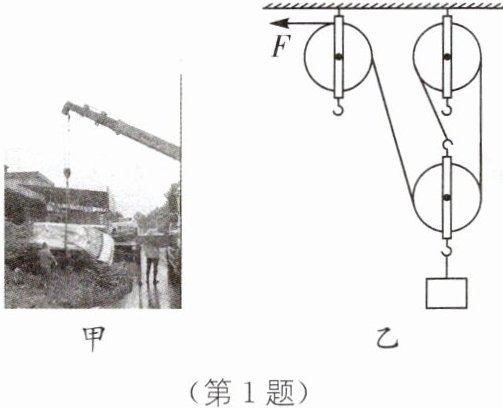
(第1题)
(1)吊车施救过程中对该车做了多少功?
(2)起重臂下滑轮组的结构如图乙所示,若钢丝绳上的拉力F为5000N,将该车向上吊起3m的过程中,拉力F的功率是多少?
(3)若不考虑钢丝绳重和摩擦,钢丝绳能承受的最大拉力是$3×10^4N,$该滑轮组能否吊起重为$8.8×10^4N$的物体?

(第1题)
答案:
1.
(1)3.6×10⁴ J
(2)7 500 W
(3)不能
[解析]
(1)根据题意,吊车施救过程中对该车做的功为W=Gh=1.2×10⁴ N×3 m=3.6×10⁴ J.
(2)由图乙可知,n=3,自由端移动的速度为v_{绳}=nv_{车}=3×0.5 m/s=1.5 m/s,拉力F的功率为P=W/t=Fs/t=Fv_{绳}=5 000 N×1.5 m/s=7 500 W.
(3)若不考虑钢丝绳重和摩擦,根据F=(1/n)(G+G_{动})可知,动滑轮重为G_{动}=nF-G=3×5 000 N-1.2×10⁴ N=3 000 N,若不考虑钢丝绳重和摩擦,钢丝绳能承受的最大拉力是3×10⁴ N,则能吊起的最大物重为G'=nF'-G_{动}=3×3×10⁴ N-3 000 N=8.7×10⁴ N<8.8×10⁴ N,故该滑轮组不能吊起重为8.8×10⁴ N的物体.
(1)3.6×10⁴ J
(2)7 500 W
(3)不能
[解析]
(1)根据题意,吊车施救过程中对该车做的功为W=Gh=1.2×10⁴ N×3 m=3.6×10⁴ J.
(2)由图乙可知,n=3,自由端移动的速度为v_{绳}=nv_{车}=3×0.5 m/s=1.5 m/s,拉力F的功率为P=W/t=Fs/t=Fv_{绳}=5 000 N×1.5 m/s=7 500 W.
(3)若不考虑钢丝绳重和摩擦,根据F=(1/n)(G+G_{动})可知,动滑轮重为G_{动}=nF-G=3×5 000 N-1.2×10⁴ N=3 000 N,若不考虑钢丝绳重和摩擦,钢丝绳能承受的最大拉力是3×10⁴ N,则能吊起的最大物重为G'=nF'-G_{动}=3×3×10⁴ N-3 000 N=8.7×10⁴ N<8.8×10⁴ N,故该滑轮组不能吊起重为8.8×10⁴ N的物体.
2. (2023·荆州中考)以“‘荆歌’铁马,奔向未来”为主题的2023荆州马拉松3月26日在荆州体育中心鸣枪起跑.在比赛场地建设过程中,工人利用长度L= 3m的斜面把质量为240kg的重物匀速推到h= 1m高处,如图所示,工人所用推力F= 1000N.g取10N/kg.
(1)求推力做的有用功.
(2)求斜面的机械效率.
(3)工人将另一质量为300kg的重物匀速推到同一高度,为了省力,换用长度为5m的斜面,此时重物与斜面间的摩擦力与原来的摩擦力之比为6:5,共用时20s,求工人推力做功的功率.
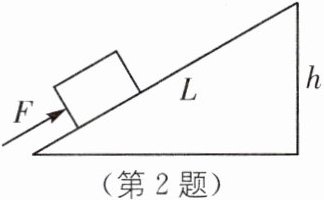
(1)求推力做的有用功.
(2)求斜面的机械效率.
(3)工人将另一质量为300kg的重物匀速推到同一高度,为了省力,换用长度为5m的斜面,此时重物与斜面间的摩擦力与原来的摩擦力之比为6:5,共用时20s,求工人推力做功的功率.

答案:
2.
(1)2 400 J
(2)80%
(3)210 W
[解析]
(1)提升重物时做的有用功W_{有用}=Gh=mgh=240 kg×10 N/kg×1 m=2 400 J.
(2)推力做的总功W_{总}=Fs=1 000 N×3 m=3 000 J,斜面的机械效率η=W_{有用}/W_{总}×100%=2 400 J/3 000 J×100%=80%.
(3)原来过程的额外功W_{额外}=W_{总}-W_{有用}=3 000 J-2 400 J=600 J,由W_{额外}=fs得重物与斜面间的摩擦力f=W_{额外}/s=600 J/3 m=200 N.工人将另一质量为300 kg的重物匀速推到同一高度,为了省力,换用长度为5 m的斜面,此时重物与斜面间的摩擦力与原来的摩擦力之比为6:5,即f'=6/5×200 N=240 N;有用功W'_{有用}=G'h=m'gh=300 kg×10 N/kg×1 m=3 000 J,额外功W'_{额外}=f's'=240 N×5 m=1 200 J,则总功W'_{总}=W'_{有用}+W'_{额外}=3 000 J+1 200 J=4 200 J;推力做功的功率P=W'_{总}/t=4 200 J/20 s=210 W.
(1)2 400 J
(2)80%
(3)210 W
[解析]
(1)提升重物时做的有用功W_{有用}=Gh=mgh=240 kg×10 N/kg×1 m=2 400 J.
(2)推力做的总功W_{总}=Fs=1 000 N×3 m=3 000 J,斜面的机械效率η=W_{有用}/W_{总}×100%=2 400 J/3 000 J×100%=80%.
(3)原来过程的额外功W_{额外}=W_{总}-W_{有用}=3 000 J-2 400 J=600 J,由W_{额外}=fs得重物与斜面间的摩擦力f=W_{额外}/s=600 J/3 m=200 N.工人将另一质量为300 kg的重物匀速推到同一高度,为了省力,换用长度为5 m的斜面,此时重物与斜面间的摩擦力与原来的摩擦力之比为6:5,即f'=6/5×200 N=240 N;有用功W'_{有用}=G'h=m'gh=300 kg×10 N/kg×1 m=3 000 J,额外功W'_{额外}=f's'=240 N×5 m=1 200 J,则总功W'_{总}=W'_{有用}+W'_{额外}=3 000 J+1 200 J=4 200 J;推力做功的功率P=W'_{总}/t=4 200 J/20 s=210 W.
3. 小梦通过如图甲所示的滑轮组将水中物体匀速提升至空中,他所用拉力F与绳子自由端移动的距离s的关系图像如图乙所示.其中物体在空中匀速上升过程中滑轮组的机械效率为85%,每个滑轮等重,不计绳重、摩擦和水的阻力.则:
(1)物体在空中上升1m,小梦做的功是多少?
(2)物体浸没在水中时所受的浮力是多少?
(3)物体在水中匀速上升过程中滑轮组的机械效率为多少?
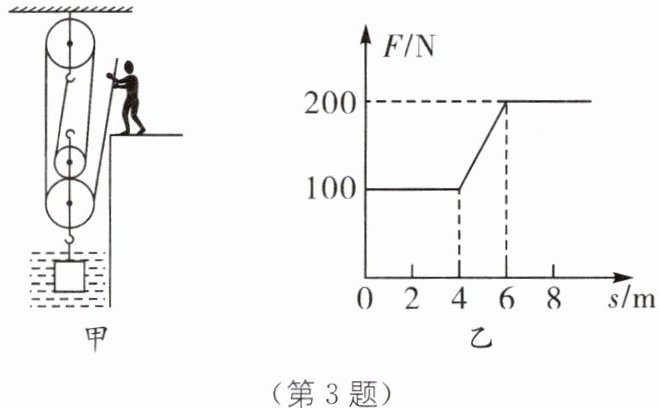
(第3题)
(1)物体在空中上升1m,小梦做的功是多少?
(2)物体浸没在水中时所受的浮力是多少?
(3)物体在水中匀速上升过程中滑轮组的机械效率为多少?

(第3题)
答案:
3.
(1)800 J
(2)400 N
(3)70%
[解析]
(1)由图乙可知,0~4 m时,拉力为100 N不变,此时物体没有露出水面,4~6 m时,物体逐渐露出水面,拉力不断增大,6~8 m时,拉力为200 N不变,此时物体完全离开水面,故物体在空中匀速上升过程中绳端的拉力F=200 N,由图可知,n=4,所以绳子自由端移动的距离s_{绳}=nh=4×1 m=4 m,小梦做的功为W_{总}=Fs_{绳}=200 N×4 m=800 J.
(2)由题知,物体在空中匀速上升过程中滑轮组的机械效率为85%,则物体在空中上升1 m,拉力所做的有用功W_{有用}=ηW_{总}=85%×800 J=680 J,由W=Gh可得,物体的重力为G=W_{有用}/h=680 J/1 m=680 N;不计绳重、摩擦和水的阻力,由W_{额外}=G_{动}h可得,动滑轮的总重力G_{动}=W_{额外}/h=(W_{总}-W_{有用})/h=(800 J-680 J)/1 m=120 N;由图乙可知,物体浸没在水中时,绳端所受拉力F₁=100 N,物体浸没在水中时,以物体和动滑轮的整体为研究对象,由力的平衡条件可得4F₁+F_{浮}=G+G_{动},则物体浸没在水中时受到的浮力F_{浮}=G+G_{动}-4F₁=680 N+120 N-4×100 N=400 N.
(3)由
(2)知,物体在水中匀速上升过程中受绳子拉力为F'_{拉}=nF₁-G_{动}=4×100 N-120 N=280 N,所以物体在水中匀速上升过程中滑轮组的机械效率为η=W_{有用}/W_{总}×100%=F'_{拉}h/F₁s×100%=F'_{拉}h/F₁nh×100%=F'_{拉}/nF₁×100%=280 N/(4×100 N)×100%=70%.
(1)800 J
(2)400 N
(3)70%
[解析]
(1)由图乙可知,0~4 m时,拉力为100 N不变,此时物体没有露出水面,4~6 m时,物体逐渐露出水面,拉力不断增大,6~8 m时,拉力为200 N不变,此时物体完全离开水面,故物体在空中匀速上升过程中绳端的拉力F=200 N,由图可知,n=4,所以绳子自由端移动的距离s_{绳}=nh=4×1 m=4 m,小梦做的功为W_{总}=Fs_{绳}=200 N×4 m=800 J.
(2)由题知,物体在空中匀速上升过程中滑轮组的机械效率为85%,则物体在空中上升1 m,拉力所做的有用功W_{有用}=ηW_{总}=85%×800 J=680 J,由W=Gh可得,物体的重力为G=W_{有用}/h=680 J/1 m=680 N;不计绳重、摩擦和水的阻力,由W_{额外}=G_{动}h可得,动滑轮的总重力G_{动}=W_{额外}/h=(W_{总}-W_{有用})/h=(800 J-680 J)/1 m=120 N;由图乙可知,物体浸没在水中时,绳端所受拉力F₁=100 N,物体浸没在水中时,以物体和动滑轮的整体为研究对象,由力的平衡条件可得4F₁+F_{浮}=G+G_{动},则物体浸没在水中时受到的浮力F_{浮}=G+G_{动}-4F₁=680 N+120 N-4×100 N=400 N.
(3)由
(2)知,物体在水中匀速上升过程中受绳子拉力为F'_{拉}=nF₁-G_{动}=4×100 N-120 N=280 N,所以物体在水中匀速上升过程中滑轮组的机械效率为η=W_{有用}/W_{总}×100%=F'_{拉}h/F₁s×100%=F'_{拉}h/F₁nh×100%=F'_{拉}/nF₁×100%=280 N/(4×100 N)×100%=70%.
查看更多完整答案,请扫码查看


