《2025年拔尖特训六年级数学上册苏教版》

(1)一个正方体的棱长扩大到原来的4倍,则其表面积扩大到原来的(16)倍。

答案： 16 解析：假设原来正方体的棱长是1，则原来的表面积是1×1×6=6；当棱长扩大到原来的4倍时，棱长就变成4，表面积就变成4×4×6=96，即其表面积扩大到原来的96÷6=16倍。

(2)一个长方体纸箱的底面是周长为20分米的正方形,它的侧面展开图正好也是一个正方形。做这个长方体纸箱至少需要(450)平方分米的硬纸板。

答案： 450 解析：长方体的侧面是指前、后、左、右四个面，根据长方体纸箱的侧面展开图是一个正方形可知，长方体的高等于长方体的底面周长，即高是20分米；长方体的底面是正方形，则底面边长是20÷4=5(分米)，即长方体的长和宽都是5分米，据此求解即可。

(3)(生活应用)王伯伯准备在墙角处搭一个正方体形状的鸡舍(两面靠墙),搭鸡舍框架用的3根钢筋一共长12m(如图)。若露在外面的面用塑料网包裹,则至少需要$( )m^2$的塑料网。


48

答案： 48

(4)用三个棱长为a米的正方体拼成一个长方体,这个长方体的表面积比原来三个正方体的表面积之和减少了(4a²)平方米。

答案： 4a² 解析：三个棱长为a米的正方体拼成的长方体，长3a米，宽a米，高a米。如图：![img alt=三个正方体拼成的长方体]，每拼一次，其表面积就减少两个边长是a米的正方形的面积之和，一共拼了2次，其表面积就减少了2a²×2=4a²(平方米)。

2. (数形结合)下面两个立体图形都是由棱长1cm的正方体搭成的。
立体图形①的表面积$= (4+7+6)×2= 34(cm^2),$其中$4cm^2、$$7cm^2、$$6cm^2$分别是从上面、前面和右面看到的图形的面积。
(1)用求立体图形①的表面积的方法,求立体图形②的表面积,列式并计算为(9+7+7)×2=46(cm²)。
(2)如果添加同样大的正方体,把立体图形②补成一个长方体,那么这个长方体的表面积至少是66$cm^2。$

答案： （1）(9+7+7)×2=46(cm²) （2）66

(1)贝贝用棱长为1厘米的小正方体摆成一个物体,从前面、右面和上面分别观察这个物体,看到的形状如图所示。这个物体的表面积是(D)平方厘米。
A. 13
B. 16
C. 28
D. 26

答案： D

(2)一个长方体的长、宽、高分别是a厘米、b厘米、c厘米。如果高增加4厘米,那么它的表面积增加(C)平方厘米。
A.4ab
B.64
C.8a+8b
D.2ab+2bc

答案： C 解析：高增加4厘米，表面积就增加了长是a厘米、宽是b厘米、高是4厘米的长方体的侧面面积。

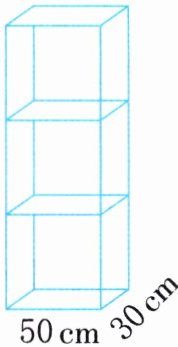
4. 妈妈买了一个三层书架(如图),书架外包装标明“50cm×30cm×150cm”。做这个书架,至少需要多少平方分米的木板？(木板材质相同,厚度忽略不计,左面、右面、后面、上面、底面及中间隔板均为木板)

答案： 50×30×4+30×150×2+50×150=22500(cm²) 22500cm²=225dm²

5. (思维过程)一个长方体(如图)的长为8厘米,上面与前面的面积之和为72平方厘米,右面的面积是上面的一半,求这个长方体的表面积。

答案： 72÷8=9(厘米) 高：8÷2=4(厘米) 宽：9-4=5(厘米) 表面积：8×5×2+8×4×2+5×4×2=184(平方厘米) 解析：已知上面的面积+前面的面积=72平方厘米，则宽与高的和为72÷8=9(厘米)。因为右面的面积是上面的一半，所以高是长的一半，即高为8÷2=4(厘米)。