《2025年拔尖特训六年级数学上册苏教版》

1. 根据图形合理推断。

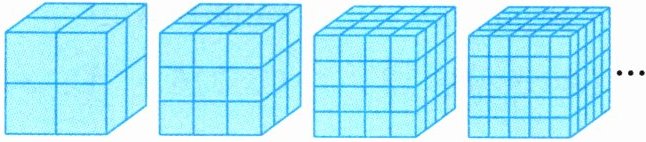
如果用n表示把大正方体的棱平均分的份数,那么：
(1)三面涂色的小正方体位于顶点上,每个顶点上有1个,共有(8)个。
(2)两面涂色的小正方体位于棱上,每条棱上有(n-2)个,共有(12(n-2))个。
(3)一面涂色的小正方体位于面上,每个面上有($(n-2)^2$)个,共有($6(n-2)^2$)个。
(4)没有涂色的小正方体位于大正方体内部,共有($(n-2)^3$)个。

答案： $1.（1）8 （2）n-2 12(n-2) （3）(n-2)^2 6(n-2)^2 （4）(n-2)^3$

2. 将一个$1dm^3$的正方体铁块的表面涂上油漆,然后切割成$1cm^3$的小正方体,在这些小正方体中,一面涂油漆的小正方体共有多少个？

答案： 2. 1dm³的正方体棱长为1dm，1cm³的正方体的棱长为$1cm 1dm=10cm (10-2)^2×6=384($个)

3. 有一个表面涂色的大正方体(包括底面),用激光把它全部切割成棱长为1厘米的小正方体,已知6面都没有涂色的小正方体有27个,则这个涂色的大正方体的体积是多少立方厘米？

答案： 3. 27=3×3×3 (3+2)×1=5(厘米) 5×5×5=125(立方厘米)

4.(探索规律)把一个表面涂色的大正方体分成若干个相同的小正方体,在所有小正方体中,3面涂色的有a个,2面涂色的有b个,1面涂色的有c个,6面都不涂色的有d个。
(1)在a、b、c、d中,(A)是固定不变的,(B)一定是12的倍数。
A. a B. b C. c D. d
(2)(B)一定是6的倍数。
A. a+b B. b+c C. c+d D. a+c
(3)当将大正方体的棱平均分成(A)份时,b、c、d相等；当将大正方体的棱平均分成(C)份时,b＜c能成立；当将大正方体的棱平均分成(C)份时,b＜d能成立。
A. 2 B. 4 C. 6 D. 以上答案都不对

答案： 4.（1）A B （2）B （3）A C C 解析：用n表示把大正方体的棱平均分的份数，则b=12(n-2)，$c=6(n-2)^2，$$d=(n-2)^3。$若要使b=c=d，即$12(n-2)=6(n-2)^2=(n-2)^3，$则当n=2时，$12×(2-2)=6×(2-2)^2=(2-2)^3=0，$符合题意。若要使b＜c，即12(n-2)＜6(n-2)^2，当n=6时，48＜96，符合题意。若要使b＜d，即12(n-2)＜(n-2)^3，当n=6时，48＜64，符合题意。

5.(模型意识)用若干个棱长a厘米的小正方体堆成如图所示的物体,然后在其表面涂上红色(不包括底面),其中3面涂色的小正方体和4面涂色的小正方体各有几个？

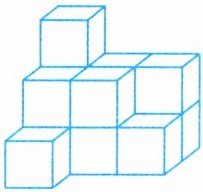
答案：
5. 3个 2个 解析：一层一层地观察，分层标出每个小正方体涂色的面数。最上层: ;中间一层: ;最下层: ，然后数出3面涂色和4面涂色的小正方体各有几个即可。

6. ★数学课上,洪老师先把一个长6厘米、宽5厘米、高4厘米的长方体的6面都涂上黄色,再把它全部切成棱长1厘米的小正方体。3面、2面、1面涂黄色的小正方体分别有多少个？

答案： 6. 3面涂黄色的小正方体：8个 2面涂黄色的小正方体：[(6-2)+(5-2)+(4-2)]×4=36(个) 1面涂黄色的小正方体：[(6-2)×(5-2)+(5-2)×(4-2)+(6-2)×(4-2)]×2=52(个) 解析：长方体上3面涂黄色的小正方体在长方体的8个顶点处，一共有8个。2面涂黄色的小正方体，在长的棱上有(6-2)×4=16(个)，在宽的棱上有(5-2)×4=12(个)，在高的棱上有(4-2)×4=8(个)，一共有16+12+8=36(个)。1面涂黄色的小正方体，上、下面有(6-2)×(5-2)×2=24(个)，左、右面有(5-2)×(4-2)×2=12(个)，前、后面有(6-2)×(4-2)×2=16(个)，一共有24+12+16=52(个)。