第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
(1)在括号里写出各数的倒数。
$\frac{6}{7}$(
1.2(
发现:当a(
$\frac{6}{7}$(
$\frac{7}{6}$
) $\frac{13}{9}$($\frac{9}{13}$
) 0.1(10
)1.2(
$\frac{5}{6}$
) 1(1
) $1\frac{2}{9}$($\frac{9}{11}$
)发现:当a(
小于1
)时,a的倒数大于a;当a(等于1
)时,a的倒数等于a;当a(大于1
)时,a的倒数小于a。(a是大于0的数)
答案:
(1)$\frac{7}{6}$ $\frac{9}{13}$ 10 $\frac{5}{6}$ 1 $\frac{9}{11}$ 小于1 等于1 大于1
(1)$\frac{7}{6}$ $\frac{9}{13}$ 10 $\frac{5}{6}$ 1 $\frac{9}{11}$ 小于1 等于1 大于1
(2)(
0
)没有倒数,最小的合数的倒数是($\frac{1}{4}$
)。
答案:
(2)0 $\frac{1}{4}$
(2)0 $\frac{1}{4}$
(3)若a、b互为倒数,则$\frac{a}{4}×b+\frac{4}{ab}$等于(
$4\frac{1}{4}$
)。
答案:
(3)$4\frac{1}{4}$
(3)$4\frac{1}{4}$
(4)已知$a×\frac{9}{8}= b×\frac{10}{13}= c×1.1= d$,且a、b、c、d均不为0,则把a、b、c、d按从大到小的顺序排列是
$b>d>c>a$
。
答案:
(4)$b>d>c>a$
(4)$b>d>c>a$
(1)下面的选项中,两个数互为倒数的是(
A.0.2和0.5
B.$1\frac{8}{7}和1\frac{7}{8}$
C.8和0.125
D.1和-1
C
)。A.0.2和0.5
B.$1\frac{8}{7}和1\frac{7}{8}$
C.8和0.125
D.1和-1
答案:
(1)C
(1)C
(2)下面的说法中,正确的是(
A.n是一个自然数,它的倒数是$\frac{1}{n}$
B.假分数的倒数一定比1小
C.在所有的质数中,2的倒数最大
D.因为$\frac{5}{7}×\frac{7}{5}= 1$,所以$\frac{5}{7}和\frac{7}{5}$都是倒数
C
)。A.n是一个自然数,它的倒数是$\frac{1}{n}$
B.假分数的倒数一定比1小
C.在所有的质数中,2的倒数最大
D.因为$\frac{5}{7}×\frac{7}{5}= 1$,所以$\frac{5}{7}和\frac{7}{5}$都是倒数
答案:
(2)C
(2)C
(3)如图,数a的倒数(
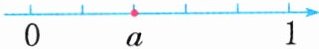
A.小于1
B.大于1
C.等于1
D.无法确定
B
)。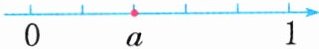
A.小于1
B.大于1
C.等于1
D.无法确定
答案:
(3)B 解析:数a在0与1之间,小于1,数a的倒数大于1。
(3)B 解析:数a在0与1之间,小于1,数a的倒数大于1。
3. 一个长方体长$\frac{9}{8}$分米,宽是长的倒数,高是长的$\frac{5}{9}$。这个长方体的体积是多少立方分米?
答案:
3.$\frac{9}{8}$×$\frac{5}{9}$=$\frac{5}{8}$(分米) $\frac{9}{8}$×$\frac{8}{9}$×$\frac{5}{8}$=$\frac{5}{8}$(立方分米)
4. (1)食堂有大米$\frac{4}{5}$吨,用去一部分后还剩$\frac{1}{3}$。还剩多少吨?
(2)食堂有大米$\frac{4}{5}$吨,用去$\frac{1}{3}$吨,还剩多少吨?
(2)食堂有大米$\frac{4}{5}$吨,用去$\frac{1}{3}$吨,还剩多少吨?
答案:
4.
(1)$\frac{4}{5}$×$\frac{1}{3}$=$\frac{4}{15}$(吨)
(2)$\frac{4}{5}$−$\frac{1}{3}$=$\frac{7}{15}$(吨)
(1)$\frac{4}{5}$×$\frac{1}{3}$=$\frac{4}{15}$(吨)
(2)$\frac{4}{5}$−$\frac{1}{3}$=$\frac{7}{15}$(吨)
5. (推理意识)三个不同质数的倒数的和是$\frac{71}{105}$,这三个质数分别是多少?
答案:
5.这三个质数分别是3、5、7 解析:设这三个质数分别是a、b、c,根据题意可知,$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$=$\frac{bc+ac+ab}{abc}$=$\frac{71}{105}$,则$abc=105$。因为$105=3×5×7$,所以这三个质数分别是3、5、7。经验证,$bc+ac+ab=71$,符合题意。
6. (思维过程)把$\frac{5}{6}$、$\frac{3}{2}$、$\frac{21}{25}$、$\frac{7}{8}$、$\frac{4}{5}$、$\frac{10}{7}$这六个数填入〇里,使每条线上3个数的乘积都是1。
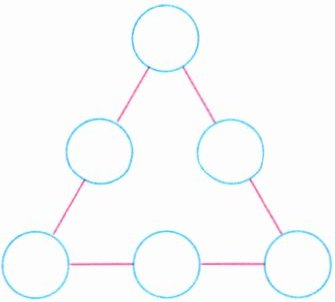

答案:
6.填法不唯一,如

解析:可将原分数的分子、分母分解质因数,通过观察数据,使每条线上3个数的乘积是1即可。如$\frac{4}{5}$×$\frac{3}{2}$×$\frac{5}{6}$=1,$\frac{5}{6}$×$\frac{21}{25}$×$\frac{10}{7}$=1,$\frac{4}{5}$×$\frac{7}{8}$×$\frac{10}{7}$=1。
6.填法不唯一,如

解析:可将原分数的分子、分母分解质因数,通过观察数据,使每条线上3个数的乘积是1即可。如$\frac{4}{5}$×$\frac{3}{2}$×$\frac{5}{6}$=1,$\frac{5}{6}$×$\frac{21}{25}$×$\frac{10}{7}$=1,$\frac{4}{5}$×$\frac{7}{8}$×$\frac{10}{7}$=1。
查看更多完整答案,请扫码查看


