《2025年拔尖特训六年级数学上册苏教版》

1. 算一算。
$\frac{2}{5}×15=$6
$35×\frac{2}{21}=$$\frac{10}{3}$
$\frac{4}{51}×34=$$\frac{8}{3}$

答案： 6 $\frac{10}{3}$ $\frac{8}{3}$

(1)(算理理解)先在图中涂出 4 个$\frac{3}{20}$,再算出涂色部分一共占这个长方形的几分之几。

($\frac{3}{20}$×4=$\frac{3}{5}$)

答案： $\frac{3}{20}$×4=$\frac{3}{5}$

(2)根据$\frac{3}{20}×\frac{△}{5}$的约分结果,可以知道$△=$8,该算式的结果是$\frac{6}{5}$。

答案： 8 $\frac{6}{5}$

(3)有一批苹果,平均每小时卖$\frac{1}{10}$,8 小时卖了这批苹果的($\frac{4}{5}$)；若平均每小时卖$\frac{1}{10}$吨,则 8 小时卖($\frac{4}{5}$)吨。

答案： $\frac{4}{5}$ $\frac{4}{5}$

(4)三名打字员分别录入同一份稿件,(王)叔叔不能 5 天内录入完这份稿件。

答案： 王

3. 一辆汽车早上$9:00$从甲地出发,$10:40$到达乙地,这辆汽车平均每分钟行驶$\frac{9}{10}$千米。甲、乙两地间的距离是多少千米？

答案： 10时40分−9时=1时40分 1时40分=100分　100×$\frac{9}{10}$=90(千米)

4.(生活应用)营养师建议每人每天食用大豆及坚果类食物$\frac{3}{100}\ kg\sim\frac{1}{25}\ kg$。
(1)按此建议,小新一家 5 口人,每天至少应该食用多少千克大豆及坚果类食物？
(2)按此建议,每人每年(按 365 天算)至少应该食用多少千克大豆及坚果类食物？

答案：
(1)$\frac{3}{100}$×5=$\frac{3}{20}$(kg)　　
(2)$\frac{3}{100}$×365=$\frac{219}{20}$(kg)　解析:根据题意，要求出5口人每天至少应该食用多少千克大豆及坚果类食物，每人每年(按365天算)至少应该食用多少千克大豆及坚果类食物，都要按每人每天食用$\frac{3}{100}$kg大豆及坚果类食物计算。

5. 一根长方体木料,长$\frac{6}{5}$米,横截面是一个面积为$\frac{3}{8}$平方米的正方形,按下图所示的方式截成 5 段,表面积增加多少平方米？

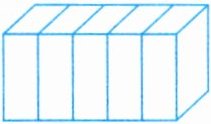
答案： 5−1=4(次)　$\frac{3}{8}$×2=$\frac{3}{4}$(平方米) $\frac{3}{4}$×4=3(平方米)

6.(探索规律)瓶子中装有一种孢子,这些孢子每小时分裂一次,每分裂一次体积增大一倍。如果最初孢子的体积占瓶子的$\frac{3}{32}$,那么 3 小时后孢子的体积占瓶子的(C)。
A.$\frac{3}{16}$
B.$\frac{3}{8}$
C.$\frac{3}{4}$
D.$\frac{3}{2}$

答案： C　解析:这种孢子每小时分裂一次，每分裂一次体积增大一倍，即这种孢子1小时体积会扩大到原来的2倍，所以3小时后，孢子的体积会扩大到原来的2×2×2=8倍，这时孢子的体积占瓶子的$\frac{3}{32}$×8=$\frac{3}{4}$。