《2025年启东中学作业本七年级数学上册人教版》

9. (2024 秋·江阴期中)如果关于 $x$ 的两个多项式 $-2x^{3}+ax^{2}-4x + b$ 与 $cx^{3}-dx + 1$ 恒等,那么 $a + b-c + d=$7.

答案： 7

10. 根据如图所示的流程图计算.
(1)若输入 $x$ 的值为 $-1$,则输出 $y$ 的值为2；
(2)若输入 $x$ 的值为 7,则输出 $y$ 的值为$\frac {5}{2}$.

答案：
(1)2
(2)$\frac {5}{2}$

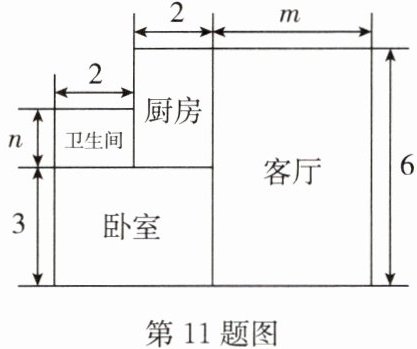
11. 小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构(单位:m)如图所示,根据图中所给的数据解答下列问题:
(1)用含 $m,n$ 的代数式表示地面的总面积；
(2)已知 $n = 1.5$,且客厅面积是卫生间面积的 8 倍,如果铺 $1m^{2}$ 地砖的平均费用为 200 元,那么铺地砖的总费用为多少元?

答案： 解:
(1)总面积为$2n+6m+3×(2+2)+2×(6-3)=(2n+6m+18)m^{2}.$
(2)因为当$n=1.5$时,客厅面积是卫生间面积的8倍,
所以$6m=8×2n=24,$
$2×1.5+24+18=45(m^{2}).$
$200×45=9000$(元).
答:铺地砖的总费用为9000元.

12. 精品书店想在甲、乙两家网店中选一家购买贺年卡,已知两家网店的贺年卡的质量相同,请阅读相关信息回答问题.
甲网店:贺年卡 1 元/张,运费 8 元,超过 30 张每张贺年卡打 6 折；
乙网店:贺年卡 0.8 元/张,运费 8 元,超过 30 张免运费.
(1)假若精品书店想购买 $x$ 张贺年卡,那么在甲、乙两家网店分别需要花多少钱? (用含有 $x$ 的式子表示)
(2)精品书店打算购买 300 张贺年卡,选择哪家网店更省钱?

答案： 解:
(1)当x不超过30时,
在甲网店需要花$(x+8)$元;
在乙网店需要花$(0.8x+8)$元.
当x超过30时,
在甲网店需要花$(0.6x+8)$元;
在乙网店需要花0.8x元.
(2)当$x=300$时,
在甲网店买需要$0.6×300+8=188$(元),
在乙网店买需要$0.8×300=240$(元).
因为$188＜240,$
所以选择甲网店更省钱.

13. 已知 $(2x - 1)^{7}= a_{0}+a_{1}x + a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}+a_{5}x^{5}+a_{6}x^{6}+a_{7}x^{7}$.
(1)求 $a_{0}-a_{1}+a_{2}-a_{3}+a_{4}-a_{5}+a_{6}-a_{7}$ 的值；
(2)求 $a_{0}+a_{2}+a_{4}+a_{6}$ 的值.

答案： 解:
(1)将$x=-1$代入原式,得
$(-2-1)^{7}=a_{0}-a_{1}+a_{2}-a_{3}+a_{4}-a_{5}+a_{6}-a_{7},$
所以$a_{0}-a_{1}+a_{2}-a_{3}+a_{4}-a_{5}+a_{6}-a_{7}=(-3)^{7}=-2187.$
(2)将$x=1$代入原式,得
$(2-1)^{7}=a_{0}+a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+a_{6}+a_{7},$
所以$a_{0}+a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+a_{6}+a_{7}=1$.①
由
(1)得$a_{0}-a_{1}+a_{2}-a_{3}+a_{4}-a_{5}+a_{6}-a_{7}=-2187$.②
①+②,得$2(a_{0}+a_{2}+a_{4}+a_{6})=-2186,$
所以$a_{0}+a_{2}+a_{4}+a_{6}=-1093.$