第107页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
6. 一种蔬菜在某市场上的批发价格如下表.
|购买数量|不超过20千克|20千克以上但不超过40千克|40千克以上|
|价格|5元/千克|4元/千克|3元/千克|
已知小明两次购买了此种蔬菜共70千克(第二次购买数量多于第一次).
(1)若第一次购买15千克,第二次购买55千克,则两次总费用为
(2)若两次购买此种蔬菜的总费用为236元,求第一次、第二次分别购买此种蔬菜多少千克?
|购买数量|不超过20千克|20千克以上但不超过40千克|40千克以上|
|价格|5元/千克|4元/千克|3元/千克|
已知小明两次购买了此种蔬菜共70千克(第二次购买数量多于第一次).
(1)若第一次购买15千克,第二次购买55千克,则两次总费用为
240
元;(2)若两次购买此种蔬菜的总费用为236元,求第一次、第二次分别购买此种蔬菜多少千克?
解:设第一次购买x千克,则第二次购买(70-x)千克.
①若第一次购买不超过20千克,则第二次购买了40千克以上.
由题意得5x+3(70-x)=236,解得x=13.
70-13=57(千克).
所以第一次购买此种蔬菜13千克,第二次购买此种蔬菜57千克.
②若第一次购买20千克以上但不超过40千克,第二次购买也为20千克以上但不超过40千克.
由题意得4x+4(70-x)=236,方程无解.
③若第一次购买20千克以上但不超过40千克,第二次购买40千克以上,
由题意得4x+3(70-x)=236,解得x=26,
70-26=44(千克).
所以第一次购买此种蔬菜26千克,第二次购买此种蔬菜44千克.
答:第一次购买此种蔬菜13千克,第二次购买此种蔬菜57千克或第一次购买此种蔬菜26千克,第二次购买此种蔬菜44千克.
①若第一次购买不超过20千克,则第二次购买了40千克以上.
由题意得5x+3(70-x)=236,解得x=13.
70-13=57(千克).
所以第一次购买此种蔬菜13千克,第二次购买此种蔬菜57千克.
②若第一次购买20千克以上但不超过40千克,第二次购买也为20千克以上但不超过40千克.
由题意得4x+4(70-x)=236,方程无解.
③若第一次购买20千克以上但不超过40千克,第二次购买40千克以上,
由题意得4x+3(70-x)=236,解得x=26,
70-26=44(千克).
所以第一次购买此种蔬菜26千克,第二次购买此种蔬菜44千克.
答:第一次购买此种蔬菜13千克,第二次购买此种蔬菜57千克或第一次购买此种蔬菜26千克,第二次购买此种蔬菜44千克.
答案:
6.
(1)240
(2)解:设第一次购买x千克,则第二次购买(70-x)千克.
①若第一次购买不超过20千克,则第二次购买了40千克以上.
由题意得5x+3(70-x)=236,解得x=13.
70-13=57(千克).
所以第一次购买此种蔬菜13千克,第二次购买此种蔬菜57千克.
②若第一次购买20千克以上但不超过40千克,第二次购买也为20千克以上但不超过40千克.
由题意得4x+4(70-x)=236,方程无解.
③若第一次购买20千克以上但不超过40千克,第二次购买40千克以上,
由题意得4x+3(70-x)=236,解得x=26,
70-26=44(千克).
所以第一次购买此种蔬菜26千克,第二次购买此种蔬菜44千克.
答:第一次购买此种蔬菜13千克,第二次购买此种蔬菜57千克或第一次购买此种蔬菜26千克,第二次购买此种蔬菜44千克.
(1)240
(2)解:设第一次购买x千克,则第二次购买(70-x)千克.
①若第一次购买不超过20千克,则第二次购买了40千克以上.
由题意得5x+3(70-x)=236,解得x=13.
70-13=57(千克).
所以第一次购买此种蔬菜13千克,第二次购买此种蔬菜57千克.
②若第一次购买20千克以上但不超过40千克,第二次购买也为20千克以上但不超过40千克.
由题意得4x+4(70-x)=236,方程无解.
③若第一次购买20千克以上但不超过40千克,第二次购买40千克以上,
由题意得4x+3(70-x)=236,解得x=26,
70-26=44(千克).
所以第一次购买此种蔬菜26千克,第二次购买此种蔬菜44千克.
答:第一次购买此种蔬菜13千克,第二次购买此种蔬菜57千克或第一次购买此种蔬菜26千克,第二次购买此种蔬菜44千克.
7. 下表是两种“5G优惠套餐”计费方式.(月费固定收,主叫不超时、流量不超量不再收费,主叫超时部分及上网超流量部分分别加收超时费和超流量费)
|计费方式|月费/元|主叫/分|流量/GB|接听|超时/(元/分)|超流量/(元/GB)|
|方式一|49|200|50|免费|0.20|3|
|方式二|69|250|65|免费|0.15|2|
(1)若某月小郭主叫通话时间为300分钟,上网流量为70GB,则她按方式一计费需
(2)若上网流量为54GB,是否存在某主叫通话时间t(分),使得按方式一和方式二的计费相等?若存在,请求出t的值;若不存在,请说明理由.
解:存在.当0≤t≤200时,49+(54-50)×3=61≠69,所以此时不存在这样的t.
当200<t≤250时,49+(t-200)×0.2+(54-50)×3=69,解得t=240.
当t>250时,49+(t-200)×0.2+(54-50)×3=69+(t-250)×0.15,
解得t=210,不合题意,舍去.
故若上网流量为54GB,当主叫通话时间为240分钟时,两种方式的计费相等.
|计费方式|月费/元|主叫/分|流量/GB|接听|超时/(元/分)|超流量/(元/GB)|
|方式一|49|200|50|免费|0.20|3|
|方式二|69|250|65|免费|0.15|2|
(1)若某月小郭主叫通话时间为300分钟,上网流量为70GB,则她按方式一计费需
129
元,按方式二计费需86.5
元.(2)若上网流量为54GB,是否存在某主叫通话时间t(分),使得按方式一和方式二的计费相等?若存在,请求出t的值;若不存在,请说明理由.
解:存在.当0≤t≤200时,49+(54-50)×3=61≠69,所以此时不存在这样的t.
当200<t≤250时,49+(t-200)×0.2+(54-50)×3=69,解得t=240.
当t>250时,49+(t-200)×0.2+(54-50)×3=69+(t-250)×0.15,
解得t=210,不合题意,舍去.
故若上网流量为54GB,当主叫通话时间为240分钟时,两种方式的计费相等.
答案:
7.
(1)129 86.5
(2)解:存在.当0≤t≤200时,49+(54-50)×3=61≠69,所以此时不存在这样的t.
当200<t≤250时,49+(t-200)×0.2+(54-50)×3=69,解得t=240.
当t>250时,49+(t-200)×0.2+(54-50)×3=69+(t-250)×0.15,
解得t=210,不合题意,舍去.
故若上网流量为54GB,当主叫通话时间为240分钟时,两种方式的计费相等.
(1)129 86.5
(2)解:存在.当0≤t≤200时,49+(54-50)×3=61≠69,所以此时不存在这样的t.
当200<t≤250时,49+(t-200)×0.2+(54-50)×3=69,解得t=240.
当t>250时,49+(t-200)×0.2+(54-50)×3=69+(t-250)×0.15,
解得t=210,不合题意,舍去.
故若上网流量为54GB,当主叫通话时间为240分钟时,两种方式的计费相等.
8. 为了缓解用电紧张,某电力公司制定了新的用电收费标准,李明根据电力公司制定的收费标准,绘制了计算程序转换机示意图(如图).
(1)李明家10月份用电190千瓦时,则应缴纳电费
(2)李明家6月份用电$x(x>210)$千瓦时,则李明家6月份应缴纳电费
(3)李明家12月份缴纳电费265元,求李明家12月份的用电量.
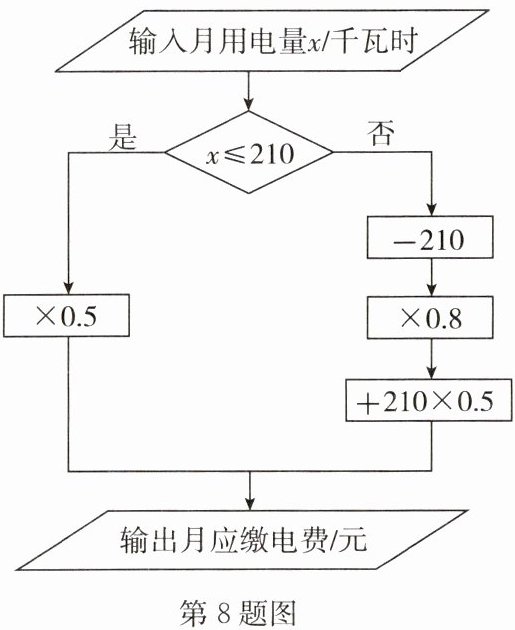
解:设李明家12月份的用电量为y千瓦时.
因为210×0.5=105(元),
105<265,所以y>210,
则0.8y-63=265,
解得y=410.
答:李明家12月份的用电量为410千瓦时.
(1)李明家10月份用电190千瓦时,则应缴纳电费
95
元;(2)李明家6月份用电$x(x>210)$千瓦时,则李明家6月份应缴纳电费
0.8x-63
元(用含x的代数式表示,并化成最简形式);(3)李明家12月份缴纳电费265元,求李明家12月份的用电量.

解:设李明家12月份的用电量为y千瓦时.
因为210×0.5=105(元),
105<265,所以y>210,
则0.8y-63=265,
解得y=410.
答:李明家12月份的用电量为410千瓦时.
答案:
8.
(1)95
(2)0.8x-63
(3)解:设李明家12月份的用电量为y千瓦时.
因为210×0.5=105(元),
105<265,所以y>210,
则0.8y-63=265,
解得y=410.
答:李明家12月份的用电量为410千瓦时.
(1)95
(2)0.8x-63
(3)解:设李明家12月份的用电量为y千瓦时.
因为210×0.5=105(元),
105<265,所以y>210,
则0.8y-63=265,
解得y=410.
答:李明家12月份的用电量为410千瓦时.
查看更多完整答案,请扫码查看


