第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
9.(12分)如图,用3个小正方形、2个中正方形、1个大正方形和缺了一个角的长方形,恰好拼成一个大长方形.根据图中数据,解答下列问题:
(1)用含$ x $的代数式表示:$ a = $
(2)当$ x = 3 $时,求大长方形的周长(可以不化简).
(1)用含$ x $的代数式表示:$ a = $
$ x+2 $
cm,$ b = $$ 2x+2 $
cm;(2)当$ x = 3 $时,求大长方形的周长(可以不化简).
解:大长方形的周长为2(3x+2a+a+b)=2[3x+2(x+2)+(x+2)+2x+2]=2×(3×3+2×5+5+2×3+2)=64(cm).
答案:
(1)x+2 2x+2
(2)解:大长方形的周长为2(3x+2a+a+b)=2[3x+2(x+2)+(x+2)+2x+2]=2×(3×3+2×5+5+2×3+2)=64(cm).
(1)x+2 2x+2
(2)解:大长方形的周长为2(3x+2a+a+b)=2[3x+2(x+2)+(x+2)+2x+2]=2×(3×3+2×5+5+2×3+2)=64(cm).
10.(20分)某公司将农副产品从公司运往市场销售,记汽车行驶的时间为$ t $h,平均速度为$ vkm/h $(汽车行驶速度不超过100km/h),$ v 随 t $的变化而变化.$ t 与 v $的几组对应值如下表:
| $ t/h $ | $ \frac{60}{19} $ | $ \frac{10}{3} $ | $ \frac{60}{17} $ | $ \frac{15}{4} $ | 4 |
| $ v/(km/h) $ | 95 | 90 | 85 | 80 | 75 |
(1)公司到市场的距离是多少千米?
(2)汽车的平均速度$ v 怎样随着行驶时间 t $的变化而变化?
(3)用式子表示$ v 与 t $之间的关系,$ v 与 t $成什么关系?
| $ t/h $ | $ \frac{60}{19} $ | $ \frac{10}{3} $ | $ \frac{60}{17} $ | $ \frac{15}{4} $ | 4 |
| $ v/(km/h) $ | 95 | 90 | 85 | 80 | 75 |
(1)公司到市场的距离是多少千米?
(2)汽车的平均速度$ v 怎样随着行驶时间 t $的变化而变化?
(3)用式子表示$ v 与 t $之间的关系,$ v 与 t $成什么关系?
答案:
解:
(1)$\frac{60}{19}×95=4×75=300(km)$,
答:公司到市场的距离是300km.
(2)汽车的平均速度v随着行驶时间t的增大而减小.
(3)$v=\frac{300}{t}$,v与t成反比例关系.
(1)$\frac{60}{19}×95=4×75=300(km)$,
答:公司到市场的距离是300km.
(2)汽车的平均速度v随着行驶时间t的增大而减小.
(3)$v=\frac{300}{t}$,v与t成反比例关系.
11.(20分)(2024秋·邳州期中)如图,这些图案是由边长相同的小正方形组成的,其中部分小正方形被有规律地涂成灰色.
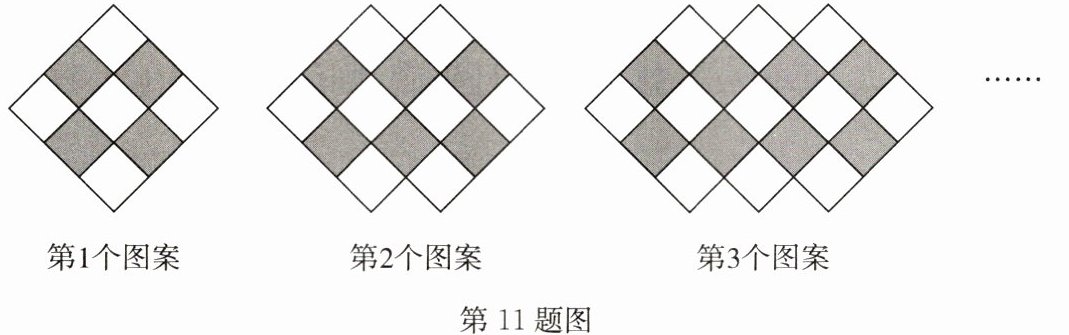
(1)填写表格:
| 序号 | 第3个图案 | 第4个图案 | 第5个图案 | … |
| 白色小正方形的数量 |
(2)第$ n $个图案中白色小正方形的数量为
(3)求第100个图案中共有多少个小正方形(两种颜色小正方形的数量之和).
解:根据所给图形可知,
第1个图案中所有小正方形的个数为9=1×5+4;
第2个图案中所有小正方形的个数为14=2×5+4;
第3个图案中所有小正方形的个数为19=3×5+4;
……
所以第n个图案中所有小正方形的个数为(5n+4).
当n=100时,5n+4=504.
即第100个图案中所有小正方形的个数为504.

(1)填写表格:
| 序号 | 第3个图案 | 第4个图案 | 第5个图案 | … |
| 白色小正方形的数量 |
11
| 14
| 17
| … |(2)第$ n $个图案中白色小正方形的数量为
3n+2
;(用含$ n $的代数式表示)(3)求第100个图案中共有多少个小正方形(两种颜色小正方形的数量之和).
解:根据所给图形可知,
第1个图案中所有小正方形的个数为9=1×5+4;
第2个图案中所有小正方形的个数为14=2×5+4;
第3个图案中所有小正方形的个数为19=3×5+4;
……
所以第n个图案中所有小正方形的个数为(5n+4).
当n=100时,5n+4=504.
即第100个图案中所有小正方形的个数为504.
答案:
(1)11 14 17
(2)3n+2
(3)解:根据所给图形可知,
第1个图案中所有小正方形的个数为9=1×5+4;
第2个图案中所有小正方形的个数为14=2×5+4;
第3个图案中所有小正方形的个数为19=3×5+4;
……
所以第n个图案中所有小正方形的个数为(5n+4).
当n=100时,5n+4=504.
即第100个图案中所有小正方形的个数为504.
(1)11 14 17
(2)3n+2
(3)解:根据所给图形可知,
第1个图案中所有小正方形的个数为9=1×5+4;
第2个图案中所有小正方形的个数为14=2×5+4;
第3个图案中所有小正方形的个数为19=3×5+4;
……
所以第n个图案中所有小正方形的个数为(5n+4).
当n=100时,5n+4=504.
即第100个图案中所有小正方形的个数为504.
查看更多完整答案,请扫码查看


