《2025年初中必刷题九年级物理上册沪粤版》

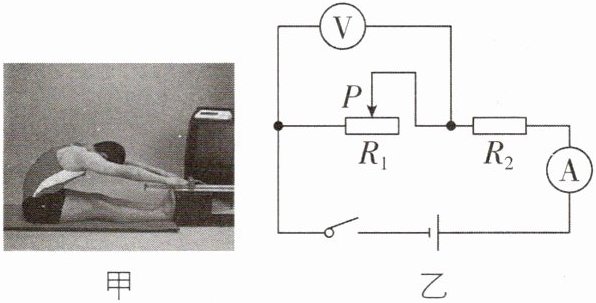
5[中]如图甲、乙是某物理兴趣小组设计的简易坐位体前屈测试仪的测试示意图和简化原理图。在测试中,测试的同学向前推动测试仪的滑块实际上是移动滑动变阻器的滑片,电压表的示数用来反映被测试者的成绩。图乙中电源电压恒为6V,电压表的测量范围为0~3V,电流表的测量范围为0~0.6A,滑动变阻器$R_{1}$标有“$15Ω$ 1A”,滑片P每移动1cm,$R_{1}接入电路的电阻变化0.5Ω$,定值电阻$R_{2}= 20Ω$。
(1)求当滑片P位于最左端时,电流表的示数。
(2)某同学测试时,从最左端推动滑片P向右移动20cm,求此时电压表的示数。
(3)既要保证电路各元件的安全,又要使滑片P能移动到最右端,则选取$R_{2}$时,其阻值不能小于多少?

答案： 5.【解】
(1)当滑片P位于最左端时，电路为定值电阻$R_2$的简单电路，根据欧姆定律可得此时通过电路的电流：$I=\frac{U}{R_2}=\frac{6V}{20\Omega}=0.3A$，即电流表示数为0.3A。
(2)滑片P每移动1cm，$R_1$接入电路的电阻变化0.5Ω，某同学测试时，从最左端推动滑片P向右移动20cm，此时滑动变阻器接入电路的电阻：$R_1 = 0.5\Omega/cm×20cm = 10\Omega$，因串联电路总电阻等于各分电阻之和，根据欧姆定律可得此时电路中的电流：$I'=\frac{U}{R_1 + R_2}=\frac{6V}{10\Omega + 20\Omega}=0.2A$，此时滑动变阻器两端的电压：$U_1 = I'R_1 = 0.2A×10\Omega = 2V$，即电压表示数为2V。
(3)当电压表示数为3V时，滑动变阻器接入电路的阻值最大，电路中电流最小，因串联电路电源电压等于各部分电压之和，所以此时定值电阻$R_2$两端的电压：$U_2 = U - U_V = 6V - 3V = 3V$，电路中最小电流：$I_{小}=\frac{U_V}{R_{1最大}}=\frac{3V}{15\Omega}=0.2A$，根据欧姆定律可得此时定值电阻的最小阻值：$R_2'=\frac{U_2}{I_{小}}=\frac{3V}{0.2A}=15\Omega$；已知电流表的测量范围为0~0.6A，滑动变阻器允许通过的最大电流为1A，根据串联电路的电流特点可知电路中的最大电流为0.6A，当滑动变阻器接入电路的阻值为0时，电路为定值电阻$R_2$的简单电路，根据欧姆定律可得此时电路中的电流：$I_{大}=\frac{U}{R_2'}=\frac{6V}{15\Omega}=0.4A＜0.6A$，所以既要保证电路各元件的安全，又要使滑片P能移动到最右端，选取$R_2$时，其阻值不能小于15Ω。

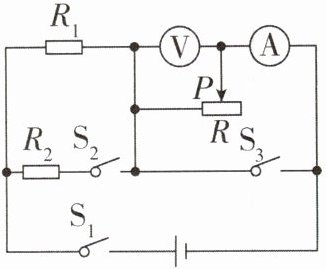
6[2024江苏南京质检,偏难]如图所示,电源电压$U = 4.5V$,定值电阻$R_{1}= 5Ω$,$R_{2}= 10Ω$,滑动变阻器R的最大阻值为$20Ω$,电压表的测量范围为0~3V,电流表的测量范围为0~0.6A。
(1)开关$S_{1}$、$S_{2}$、$S_{3}$均闭合时,求电路中的电流。
(2)$S_{1}$闭合,$S_{2}$、$S_{3}$断开,为保证电路元件安全,求滑动变阻器R能接入电路的阻值范围。

答案： 6.【解】
(1)当开关$S_1$、$S_2$、$S_3$均闭合时，$R_1$与$R_2$并联，由并联电路的电压规律可知，$U_1 = U_2 = U = 4.5V$，由$I=\frac{U}{R}$和并联电路的电流特点知，电路中的电流$I = I_1 + I_2=\frac{U}{R_1}+\frac{U}{R_2}=\frac{4.5V}{5\Omega}+\frac{4.5V}{10\Omega}=1.35A$。
(2)当$S_1$闭合，$S_2$、$S_3$断开时，$R_1$与变阻器R串联，电压表测变阻器R两端电压，当R接入电路的电阻最小时电路中的电流最大，$I_{max}=0.6A$，电路的总电阻$R_{总}=\frac{U}{I_{max}}=\frac{4.5V}{0.6A}=7.5\Omega$，根据串联电路的电阻规律可得，变阻器接入电路的最小阻值$R_{min}=R_{总}-R_1 = 7.5\Omega - 5\Omega = 2.5\Omega$；当变阻器R两端电压达到$U_{max}=3V$时电路中电流最小，$I_{min}=\frac{U - U_{max}}{R_1}=\frac{4.5V - 3V}{5\Omega}=0.3A$，此时变阻器接入电路的阻值最大，$R_{max}=\frac{U_{max}}{I_{min}}=\frac{3V}{0.3A}=10\Omega$，故滑动变阻器R能接入电路的阻值范围为2.5~10Ω。

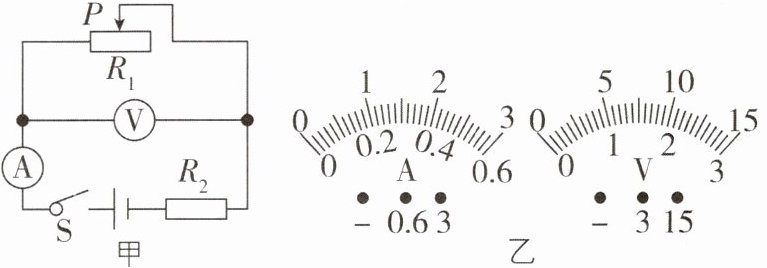
7[2024河北承德期末,难]在图甲所示的电路中,电源电压为6V不变,滑动变阻器$R_{1}$上标有“$10Ω$ 1A”字样,电阻$R_{2}的阻值为5Ω$,电压表的测量范围为0~15V,电流表的测量范围为0~0.6A。闭合开关S,电流表的示数为0.4A。
(1)求电压表的示数及滑动变阻器连入电路中的阻值。
(2)如果电源电压可以改变,选择合适的电表量程,移动滑片P,使如图乙所示的两个电表的指针都能达到满偏,求符合上述要求的电源电压的变化范围。

答案： 7.【解】
(1)由图甲可知，闭合开关S，$R_1$和$R_2$串联，电压表测$R_1$两端电压，电流表测电路中的电流，则$R_2$两端的电压$U_2 = IR_2 = 0.4A×5\Omega = 2V$，根据串联电路的电压规律可知，电压表示数$U_1 = U - U_2 = 6V - 2V = 4V$；滑动变阻器连入电路中的阻值$R_1=\frac{U_1}{I}=\frac{4V}{0.4A}=10\Omega$。
(2)由题意可知，滑动变阻器允许通过的最大电流为1A，电流表能够达到满偏，故电流表应选择0~0.6A量程，为使电流表达到满偏，则电源电压至少为$U' = I_{A大}R_2 = 0.6A×5\Omega = 3V$，若电压表选择0~15V量程，因电压表能满偏，则电压表的最大示数为15V，且变阻器接入电路的阻值最大为10Ω，则电压表满偏时电路中的电流至少为$I_{小}=\frac{U_{V大}}{R_{1大}}=\frac{15V}{10\Omega}=1.5A＞0.6A$，所以电压表选择0~3V量程；当电压表和电流表同时满偏时，电压表、电流表的示数都最大，此时滑动变阻器接入电路的阻值为$R_1'=\frac{U_{Vmax}}{I_{max}}=\frac{3V}{0.6A}=5\Omega＜10\Omega$，由$U = IR$可知此时定值电阻$R_2$两端的电压最大，电源电压最大，由串联电路的电压特点和欧姆定律可得，最大电源电压$U_{总max}=U_{Vmax}+U_{2max}=U_{Vmax}+I_{max}R_2 = 3V + 0.6A×5\Omega = 6V$；当电压表示数最大为3V(此时电压表满偏)，且滑动变阻器接入电路的阻值为10Ω时，电路中的电流最小，此时定值电阻$R_2$两端的电压最小，电源电压最小，电路中的最小电流$I_{min}=\frac{U_{Vmax}}{R_{1大}}=\frac{3V}{10\Omega}=0.3A$，则最小电源电压$U_{总min}=U_{Vmax}+U_{2min}=U_{Vmax}+I_{min}R_2 = 3V + 0.3A×5\Omega = 4.5V＞3V$，所以电源电压的变化范围为4.5~6V。