第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
如图所示,小明重500 N,他用手托着一个重为5 N的篮球乘坐厢式电梯,电梯匀速上升了10 m。下列关于小明和厢式电梯做功的说法正确的是(
A.小明托篮球的力没有对篮球做功
B.厢式电梯对小明的支持力对小明做功50 J
C.小明托篮球的力对篮球做功50 J
D.厢式电梯对小明的支持力没有对小明做功
C
)A.小明托篮球的力没有对篮球做功
B.厢式电梯对小明的支持力对小明做功50 J
C.小明托篮球的力对篮球做功50 J
D.厢式电梯对小明的支持力没有对小明做功
答案:
C 【解析】小明托着篮球跟电梯一起匀速上升了10 m,托篮球的力方向竖直向上,满足力做功的条件,因此小明托篮球的力对篮球做了功,故A错误;厢式电梯对小明的支持力方向竖直向上,小明在力的方向上移动了10 m,因此厢式电梯对小明的支持力对小明做功,故D错误;小明匀速上升,厢式电梯对小明的支持力等于小明和篮球的总重力,即$F=500\ \text{N}+5\ \text{N}=505\ \text{N}$,厢式电梯对小明的支持力对小明做功为$W=Fs=505\ \text{N}× 10\ \text{m}=5050\ \text{J}$,故B错误;小明托篮球的力对篮球做功为$W_{\text{托}}=F_{\text{托}}s=5\ \text{N}× 10\ \text{m}=50\ \text{J}$,故C正确。故选C。
2 [中]甲、乙两物体分别在水平拉力的作用下沿水平方向做匀速直线运动,若甲的质量是乙的2倍,甲受到的水平拉力是乙的3倍,甲的速度是乙的4倍,那么在相同的时间内,拉力对甲、乙两物体做功之比为(
A.3:1
B.6:1
C.12:1
D.24:1
C
)A.3:1
B.6:1
C.12:1
D.24:1
答案:
C 【解析】由$v=\frac{s}{t}$得,相同时间内甲、乙两物体运动的距离之比$s_{\text{甲}}:s_{\text{乙}}=v_{\text{甲}}t:(v_{\text{乙}}t)=v_{\text{甲}}:v_{\text{乙}}=4:1$,拉力对甲、乙做功之比$W_{\text{甲}}:W_{\text{乙}}=F_{\text{甲}}s_{\text{甲}}:(F_{\text{乙}}s_{\text{乙}})=3× 4:(1× 1)=12:1$。故选C。
3 [2025安徽亳州调研,中]如图所示,在水平拉力F的作用下,重40 N的物体A沿水平地面匀速移动了10 m,物体A受到地面的摩擦力为5 N,不计滑轮、绳子的重力及滑轮与绳子间的摩擦,拉力F做的功为(
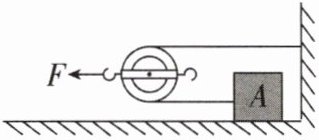
A.50 J
B.25 J
C.100 J
D.200 J
A
)
A.50 J
B.25 J
C.100 J
D.200 J
答案:
A 【解析】不计滑轮、绳子的重力及滑轮与绳子间的摩擦,物体A做匀速直线运动,受到绳子的拉力等于地面对A的摩擦力,拉力F作用在动滑轮上,则拉力$F=2F_{\text{绳}}=2f=2× 5\ \text{N}=10\ \text{N}$,拉力F的作用点移动的距离$s'=\frac{1}{2}s=\frac{1}{2}× 10\ \text{m}=5\ \text{m}$,拉力F做的功$W=Fs'=10\ \text{N}× 5\ \text{m}=50\ \text{J}$。故选A。
4 [2023湖南株洲中考,偏难](多选)某建筑工地上,一台起重机将两种材料同时从地面竖直匀速起吊送至两个不同的高度,整个过程中起重机提升材料所做的功W与提升高度h的关系如图所示。由图可知(g取10 N/kg)(
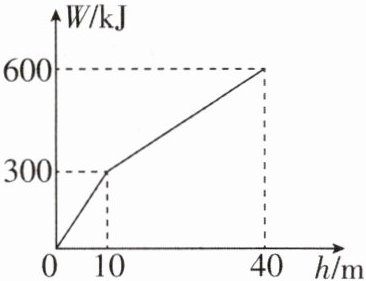
A.两种材料总质量为1.5 t
B.两种材料总质量为3 t
C.吊到40 m高处的材料质量为1 t
D.吊到40 m高处的材料质量为1.5 t
BC
)
A.两种材料总质量为1.5 t
B.两种材料总质量为3 t
C.吊到40 m高处的材料质量为1 t
D.吊到40 m高处的材料质量为1.5 t
答案:
BC 【解析】由图可知,起重机将两种材料同时从地面竖直匀速起吊送至10 m高处时,提升材料所做的功为$W_1=300\ \text{kJ}=3× 10^5\ \text{J}$,由$W=Gh$得,两种材料的总重力为$G_{\text{总}}=\frac{W_1}{h_1}=\frac{3× 10^5\ \text{J}}{10\ \text{m}}=3× 10^4\ \text{N}$,由$G=mg$得,两种材料的总质量为$m_{\text{总}}=\frac{G_{\text{总}}}{g}=\frac{3× 10^4\ \text{N}}{10\ \text{N/kg}}=3× 10^3\ \text{kg}=3\ \text{t}$,故A错误,B正确;由图可知,起重机将吊到40 m高处的材料从10 m高处送至40 m高处时,提升材料所做的功为$W_2=600\ \text{kJ}-300\ \text{kJ}=300\ \text{kJ}=3× 10^5\ \text{J}$,由$W=Gh$得,吊到40 m高处的材料的重力为$G=\frac{W_2}{h_2}=\frac{3× 10^5\ \text{J}}{40\ \text{m}-10\ \text{m}}=1× 10^4\ \text{N}$,由$G=mg$得,吊到40 m高处的材料的质量为$m=\frac{G}{g}=\frac{1× 10^4\ \text{N}}{10\ \text{N/kg}}=1× 10^3\ \text{kg}=1\ \text{t}$,故C正确,D错误。故选BC。
一个重200 N的物体在大小不变的水平拉力的作用下匀速直线前进了25 m,拉力撤掉后,物体由于惯性又前进了10 m。在物体向前运动35 m的过程中拉力做的功为700 J,则水平拉力的大小为
28
N,此过程中重力做的功是0
J,物体靠惯性运动10 m的过程中克服摩擦力做的功是280
J。
答案:
28 0 280 【解析】物体在水平拉力的作用下移动的距离$s=25\ \text{m}$,水平拉力所做的功$W=700\ \text{J}$,所以拉力的大小为$F=\frac{W}{s}=\frac{700\ \text{J}}{25\ \text{m}}=28\ \text{N}$;物体在重力的方向上没有移动距离,因此重力对物体没有做功,即重力做的功为0 J;物体在水平拉力作用下匀速直线前进,由平衡力知识可知物体受到的摩擦力$f=F=28\ \text{N}$,则物体靠惯性运动10 m的过程中克服摩擦力做的功是$W'=fs'=28\ \text{N}× 10\ \text{m}=280\ \text{J}$。
6 [2025江西宜春调研,中]如图甲为集自动清扫技术和人工智能设计于一体的地面清扫机器人,可以将灰尘吸入集尘盒。机器人扫地时所受阻力与速度的关系如图乙,若该机器人在1 min内沿直线匀速清扫地面的距离为12 m,求:
(1)该机器人清扫地面时的移动速度;
(2)1 min内该机器人的动力所做的功。
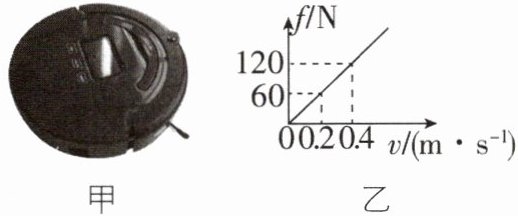
(1)该机器人清扫地面时的移动速度;
(2)1 min内该机器人的动力所做的功。

答案:
【解】
(1)该机器人清扫地面时的移动速度为$v=\frac{s}{t}=\frac{12\ \text{m}}{60\ \text{s}}=0.2\ \text{m/s}$;
(2)由图乙可知,当机器人的速度$v=0.2\ \text{m/s}$时,所受阻力$f=60\ \text{N}$,机器人做匀速直线运动,故机器人的动力$F=f=60\ \text{N}$,则1 min内动力所做的功为$W=Fs=60\ \text{N}× 12\ \text{m}=720\ \text{J}$。
(1)该机器人清扫地面时的移动速度为$v=\frac{s}{t}=\frac{12\ \text{m}}{60\ \text{s}}=0.2\ \text{m/s}$;
(2)由图乙可知,当机器人的速度$v=0.2\ \text{m/s}$时,所受阻力$f=60\ \text{N}$,机器人做匀速直线运动,故机器人的动力$F=f=60\ \text{N}$,则1 min内动力所做的功为$W=Fs=60\ \text{N}× 12\ \text{m}=720\ \text{J}$。
7 核心素养科学思维[中]如图所示,需要把一放置在水平地面上的重为400 N、棱长为1 m、质量分布均匀的实心正方体,利用翻滚的方法沿直线移动10 m。则在这一过程中该正方体克服重力做的功为______。($\sqrt{2}$取1.414)
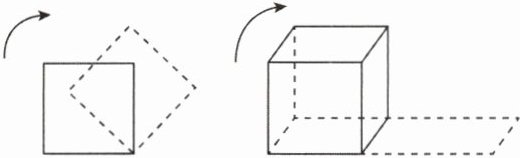

828 J
答案:
828 J 【解析】平放在水平地面上的正方体的重心的高度为$h=\frac{1}{2}a=\frac{1}{2}× 1\ \text{m}=\frac{1}{2}\ \text{m}$,正方体表面的对角线的长度为$l=\sqrt{a^2+a^2}=\sqrt{(1\ \text{m})^2+(1\ \text{m})^2}=\sqrt{2}\ \text{m}$;滚动时,重心上升到的最大高度为$h'=\frac{1}{2}l=\frac{1}{2}× \sqrt{2}\ \text{m}=\frac{\sqrt{2}}{2}\ \text{m}$,滚动时重心升高的最大高度为$\Delta h=h'-h=\frac{\sqrt{2}}{2}\ \text{m}-\frac{1}{2}\ \text{m}=\frac{\sqrt{2}-1}{2}\ \text{m}$,翻滚一次克服重力做的功为$W=G\Delta h=400\ \text{N}× \frac{\sqrt{2}-1}{2}\ \text{m}=82.8\ \text{J}$,移动10 m,要翻滚10次,所以这一过程克服重力做的功$W_G=10W=10× 82.8\ \text{J}=828\ \text{J}$。
查看更多完整答案,请扫码查看


