《2025年初中必刷题九年级物理上册沪粤版》

如图为古书中记载的一种斜面引重车。绳子一端紧系在后轮上,另一端绕过斜面顶端的滑轮与重物相连。推车前行,重物被绳子从斜面底端缓慢匀速提升至斜面顶端。若物重为4000N,斜面长2m,高0.8m,后轮施加在绳子上的力为2000N(不计绳重、滑轮与绳间的摩擦),则该斜面的机械效率为80%,重物与斜面之间的摩擦力是400N。

答案： 80 400 【解析】有用功$W_{有}=Gh=4000N×0.8m=3200J$，总功$W_{总}=Fs=2000N×2m=4000J$，则该斜面的机械效率$η=\frac {W_{有}}{W_{总}}=\frac {3200J}{4000J}=80\% $，额外功$W_{额}=W_{总}-W_{有}=4000J-3200J=800J$，则重物与斜面之间的摩擦力$f=\frac {W_{额}}{s}=\frac {800J}{2m}=400N$。

(1)在这个实验中,可以通过观察铁钉插入泡沫塑料的深度来比较铝块重力势能的大小。
(2)甲、乙实验说明在质量相同时，物体所处位置越高，重力势能越大；比较甲、丙实验的情况,说明铝块所处位置相同时,质量越大,铝块的重力势能越大。
(3)分析上述实验,得出的结论是：物体的高度越高、质量越大,它的重力势能越大。

答案：
(1)铁钉插入泡沫塑料的深度
(2)在质量相同时，物体所处位置越高，重力势能越大 甲、丙
(3)物体的高度越高、质量越大 【解析】
(1)本实验中是通过观察铁钉插入泡沫塑料的深度来比较铝块重力势能大小的，这是转换法的应用。
(2)甲、乙实验中，两个铝块质量相同，铝块所处位置越高，铁钉插入泡沫塑料的深度越深，铝块重力势能越大，所以得到的结论是：在质量相同时，物体所处位置越高，重力势能越大；探究重力势能的大小与质量的关系时，需要控制铝块下落的高度相同，铝块的质量不同，故需要对比甲、丙两次实验。
(3)分析上述实验可知，物体的高度越高、质量越大，它的重力势能越大。

(1)根据表中数据可以判断出第1次实验选择的是甲(填“甲”或“乙”)滑轮组。
(2)在第1次实验中,当竖直向上匀速拉动滑轮组时,弹簧测力计示数如图丙所示,则拉力F为0.4N,该次实验中滑轮组的机械效率是41.7%(计算结果精确到0.1%)。

答案：
(1)甲
(2)竖直向上匀速 0.4 41.7% 【解析】
(1)由表中第 1 次实验数据可知，钩码上升的高度$h=10cm$，绳端移动的距离$s=30cm$，由$s=nh$可得，绳子的有效股数$n=\frac {s}{h}=\frac {30cm}{10cm}=3$，由题图可知，甲滑轮组绳子的有效股数为 3，乙滑轮组绳子的有效股数为 4，所以，第 1 次实验选择的是甲滑轮组。
(2)实验时要竖直向上匀速拉动弹簧测力计；由题图丙可知，弹簧测力计的分度值为 0.2 N，拉力 F 为 0.4 N，该次实验滑轮组的机械效率$η=\frac {W_{有}}{W_{总}}×100\% =\frac {0.5N×0.1m}{0.4N×0.3m}×100\% \approx 41.7\% $。

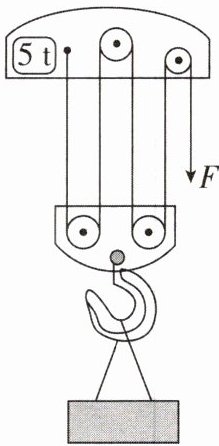
10[2024江苏苏州中考,中]某起重机的滑轮组结构示意如图所示,其最大载重为5t。起重机将3600kg的钢板匀速提升到10m高的桥墩上,滑轮组的机械效率为80%。不计钢丝绳的重力和摩擦,g取10N/kg。求：
(1)克服钢板重力做的功W_有用；
(2)钢丝绳的拉力F；
(3)滑轮组满载时的机械效率(保留一位小数)。

答案： 【解】
(1)克服钢板重力做的功$W_{有}=Gh=mgh=3600kg×10N/kg×10m=3.6×10^{5}J$。
(2)由图可知$n=4$，由$η=\frac {W_{有}}{W_{总}}$可知，总功$W_{总}=\frac {W_{有}}{η}=\frac {3.6×10^{5}J}{80\% }=4.5×10^{5}J$，根据总功$W_{总}=Fs=Fnh$知，拉力$F=\frac {W_{总}}{nh}=\frac {4.5×10^{5}J}{4×10m}=1.125×10^{4}N$。
(3)不计钢丝绳的重力和摩擦，$W_{额}=W_{总}-W_{有}=4.5×10^{5}J-3.6×10^{5}J=0.9×10^{5}J$，根据$W_{额}=G_{动}h$可知，动滑轮以及吊钩部分的总重力$G_{动}=\frac {W_{额}}{h}=\frac {0.9×10^{5}J}{10m}=9000N$，滑轮组满载时的机械效率$η'=\frac {W'_{有}}{W'_{总}}×100\% =\frac {G_{max}h}{G_{max}h+G_{动}h}×100\% =\frac {G_{max}}{G_{max}+G_{动}}×100\% =\frac {5×10^{3}kg×10N/kg}{5×10^{3}kg×10N/kg+9000N}×100\% \approx 84.7\% $。