第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
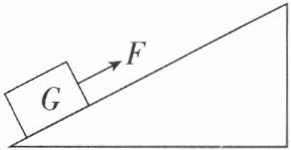
1[2024江西宜春期末]如图,重为G的物体在沿斜面向上的拉力作用下,从斜面的底部移到顶部,设沿斜面移动的距离为s,斜面的高为h,拉力为F,物体受到的摩擦力为f,则斜面的机械效率为(
A.$\frac{Gh}{fs}$
B.$\frac{Gh}{Fs}$
C.$\frac{Gh}{(F + f)s}$
D.$\frac{Gh}{(F - f)s}$
B
)
A.$\frac{Gh}{fs}$
B.$\frac{Gh}{Fs}$
C.$\frac{Gh}{(F + f)s}$
D.$\frac{Gh}{(F - f)s}$
答案:
B 【解析】此过程中,有用功为$W_{有用}=Gh$,总功为$W_{总}=Fs$,则斜面的机械效率为$\eta =\frac {W_{有用}}{W_{总}}=\frac {Gh}{Fs}$,故 B 正确。
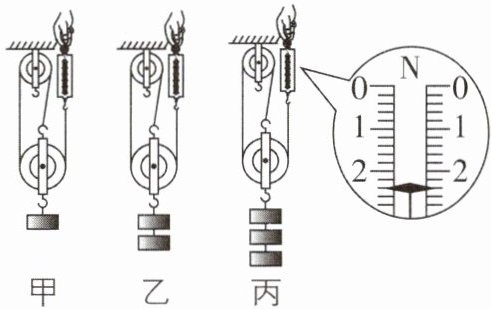
在“测量滑轮组的机械效率”实验中,小丽用如图所示的同一滑轮组提升不同钩码,分别做了下面的实验,实验数据记录如表(每个钩码所受重力为2N)。
|实验次数|钩码所受的重力G/N|提升高度h/m|拉力F/N|绳端移动的距离s/m|机械效率η|
|1|2|0.05|1.0|0.15|66.7%|
|2|2|0.10|1.0|0.30|66.7%|
|3|4|0.10|1.7|0.30|78.4%|
|4|6|0.10|①|0.30|②|
(1)实验中要竖直向上
(2)第4次实验的弹簧测力计示数如图丙所示,则表格中编号①处数据应为
(3)比较第
(4)分析以上实验数据可以得出如下结论:同一滑轮组的机械效率与
(5)若将此滑轮组换一种绕绳方法,不计摩擦及绳重,提升相同的物体时,滑轮组的机械效率

|实验次数|钩码所受的重力G/N|提升高度h/m|拉力F/N|绳端移动的距离s/m|机械效率η|
|1|2|0.05|1.0|0.15|66.7%|
|2|2|0.10|1.0|0.30|66.7%|
|3|4|0.10|1.7|0.30|78.4%|
|4|6|0.10|①|0.30|②|
(1)实验中要竖直向上
匀速
拉动弹簧测力计,使钩码升高。(2)第4次实验的弹簧测力计示数如图丙所示,则表格中编号①处数据应为
2.4
,编号②处数据应为83.3%
。(3)比较第
1、2
两次实验,小丽同学发现:同一滑轮组的机械效率与重物被提升的高度无关
(填“有关”或“无关”)。(4)分析以上实验数据可以得出如下结论:同一滑轮组的机械效率与
被提升物体的重力
有关。(5)若将此滑轮组换一种绕绳方法,不计摩擦及绳重,提升相同的物体时,滑轮组的机械效率
不变
(填“变大”“变小”或“不变”)。
答案:
(1)匀速
(2)2.4 83.3%
(3)1、2 无关
(4)被提升物体的重力
(5)不变
【解析】
(1)实验中要竖直向上匀速拉动弹簧测力计。
(2)由图丙知,弹簧测力计的分度值为0.2 N,则第4次的拉力为2.4 N,表格中编号①处数据应为2.4;由表中数据可得,第4次实验的机械效率$\eta =\frac {W_{有用}}{W_{总}}×100\% =\frac {Gh}{Fs}×100\% =\frac {6N×0.10m}{2.4N×0.30m}×100\% \approx 83.3\% $。
(3)研究同一滑轮组的机械效率与重物被提升的高度的关系,要控制被提升物体的重力相同,提升高度不同,比较第1、2两次实验,提升钩码的重力相同,高度不同,但机械效率相同,故同一滑轮组的机械效率与重物被提升的高度无关。
(4)由表中数据可知,使用同一滑轮组,提升物体的重力越大,机械效率越高,即同一滑轮组的机械效率与被提升物体的重力有关。
(5)不计摩擦及绳重,额外功为克服动滑轮重力所做的功,滑轮组的机械效率$η'=\frac {Gh}{Gh+G_{动}h}×100\% =\frac {G}{G+G_{动}}×100\% $,若将此滑轮组换一种绕绳方法,物重和动滑轮重不变,所以滑轮组的机械效率不变。
(1)匀速
(2)2.4 83.3%
(3)1、2 无关
(4)被提升物体的重力
(5)不变
【解析】
(1)实验中要竖直向上匀速拉动弹簧测力计。
(2)由图丙知,弹簧测力计的分度值为0.2 N,则第4次的拉力为2.4 N,表格中编号①处数据应为2.4;由表中数据可得,第4次实验的机械效率$\eta =\frac {W_{有用}}{W_{总}}×100\% =\frac {Gh}{Fs}×100\% =\frac {6N×0.10m}{2.4N×0.30m}×100\% \approx 83.3\% $。
(3)研究同一滑轮组的机械效率与重物被提升的高度的关系,要控制被提升物体的重力相同,提升高度不同,比较第1、2两次实验,提升钩码的重力相同,高度不同,但机械效率相同,故同一滑轮组的机械效率与重物被提升的高度无关。
(4)由表中数据可知,使用同一滑轮组,提升物体的重力越大,机械效率越高,即同一滑轮组的机械效率与被提升物体的重力有关。
(5)不计摩擦及绳重,额外功为克服动滑轮重力所做的功,滑轮组的机械效率$η'=\frac {Gh}{Gh+G_{动}h}×100\% =\frac {G}{G+G_{动}}×100\% $,若将此滑轮组换一种绕绳方法,物重和动滑轮重不变,所以滑轮组的机械效率不变。
3[2025安徽池州调研]用同一滑轮组竖直提升物体,小明提出了三种提高滑轮组机械效率的方法,可行的是(
①使用轻质的动滑轮 ②用滑轮组提升很轻的物体 ③在滑轮的轮与轴之间注些润滑油
A.①②
B.①③
C.②
D.①②③
B
)①使用轻质的动滑轮 ②用滑轮组提升很轻的物体 ③在滑轮的轮与轴之间注些润滑油
A.①②
B.①③
C.②
D.①②③
答案:
B 【解析】根据机械效率的定义可知$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {W_{有用}}{W_{有用}+W_{额}}×100\% =\frac {1}{1+\frac {W_{额}}{W_{有用}}}×100\% $,若要提高滑轮组机械效率,可以增大有用功或者减小额外功。使用轻质的动滑轮和在滑轮的轮与轴之间注些润滑油可以减小额外功,能提高机械效率;用滑轮组提升很轻的物体时有用功减小,额外功几乎不变,机械效率会降低。综上所述,①③可以提高机械效率,故选 B。
4如图所示,用滑轮组将物体匀速提升,不计绳重及摩擦,下列措施可提高该滑轮组机械效率的是(
A.增加1个动滑轮
B.改变绕线方式
C.增加物体被提升的高度
D.增大提升的物体的重力
D
)A.增加1个动滑轮
B.改变绕线方式
C.增加物体被提升的高度
D.增大提升的物体的重力
答案:
D 【解析】用滑轮组匀速提升物体时,有用功为$W_{有用}=Gh$,不计绳重和摩擦,额外功为$W_{额}=G_{动}h$,总功为$W_{总}=W_{有用}+W_{额}=Gh+G_{动}h$,则滑轮组的机械效率:$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {Gh}{Gh+G_{动}h}×100\% =\frac {G}{G+G_{动}}×100\% =\frac {1}{1+\frac {G_{动}}{G}}×100\% $,由此可知,滑轮组机械效率的高低与物体被提升的高度和绕线方式都无关,故 B、C 错误;由上式可知,物体重力不变,增加一个动滑轮,动滑轮的总重力增大,滑轮组的机械效率减小,故 A 错误;在动滑轮重力不变的情况下,增大提升的物体的重力,可以增大机械效率,故 D 正确。
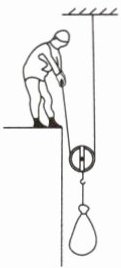
5如图所示,利用动滑轮提升货物,动滑轮重为20N,滑轮与轴之间的摩擦及绳重不计。第一次把重为100N的货物匀速提升,这个过程中动滑轮的机械效率为$\eta_{1}$;第二次把重为200N的货物匀速提升,这个过程中动滑轮的机械效率为$\eta_{2}$。则(
A.$\eta_{1}>\eta_{2}$
B.$\eta_{1}<\eta_{2}$
C.$\eta_{1}= \eta_{2}$
D.无法确定$\eta_{1}和\eta_{2}$的关系
B
)
A.$\eta_{1}>\eta_{2}$
B.$\eta_{1}<\eta_{2}$
C.$\eta_{1}= \eta_{2}$
D.无法确定$\eta_{1}和\eta_{2}$的关系
答案:
B 【解析】两次提升货物用的是同一个动滑轮,滑轮与轴之间的摩擦及绳重不计,由公式$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {G_{物}h}{G_{物}h+G_{轮}h}×100\% =\frac {G_{物}}{G_{物}+G_{轮}}×100\% =\frac {1}{1+\frac {G_{轮}}{G_{物}}}×100\% $可得,由于$G_{物1}<G_{物2},G_{轮}$不变,所以$η_{1}<η_{2}$,故 B 正确。
查看更多完整答案,请扫码查看


