第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
如图,为了提升重物,我们选用了粗细均匀、重力为G的杠杆,不计杠杆支点处的摩擦,先后把同一个重物挂在A、B两点,每次让杠杆上升同样的高度,下列说法正确的是(
A.重物在A点时动力做的有用功多,杠杆的机械效率高
B.重物在A点和B点杠杆的机械效率相等
C.重物在B点时动力做的有用功多,杠杆的机械效率高
D.重物在B点时动力做的额外功多,杠杆的机械效率高
C
)A.重物在A点时动力做的有用功多,杠杆的机械效率高
B.重物在A点和B点杠杆的机械效率相等
C.重物在B点时动力做的有用功多,杠杆的机械效率高
D.重物在B点时动力做的额外功多,杠杆的机械效率高
答案:
C 【解析】利用杠杆提升重物,有用功$W_{有用}=G_{物}h$,提升的是同一个重物,每次杠杆上升同样的高度,重物上升的高度$h_{B}>h_{A}$,重物在 A、B 两点有用功不相同,重物在 A 点时动力做的有用功少,故 A 选项错误。由图可知,每次让杠杆上升同样的高度,杠杆重心上升的高度$h'_{A}=h'_{B}$,不计杠杆支点处的摩擦,$W_{额外A}=W_{额外B}$,故 D 选项错误。重物在 A、B 两点被提升的高度不同,做的有用功不相同,而$W_{总}=W_{有用}+W_{额外}$,即$W_{总A}<W_{总B}$,由$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {W_{有用}}{W_{有用}+W_{额外}}×100\% =\frac {1}{1+\frac {W_{额外}}{W_{有用}}}×100\% $可得$η_{A}<η_{B}$,故 B 选项错误,C 选项正确。故选 C。
2新考法[2025广东广州期中,中]如图甲所示,A、B是两个体积完全相同的物体,小明和小芳分别用大小不变的拉力$F_{A}和F_{B}$,用相同的时间分别将A、B两物体拉到斜面顶端,对物体做功情况如图乙所示,则(
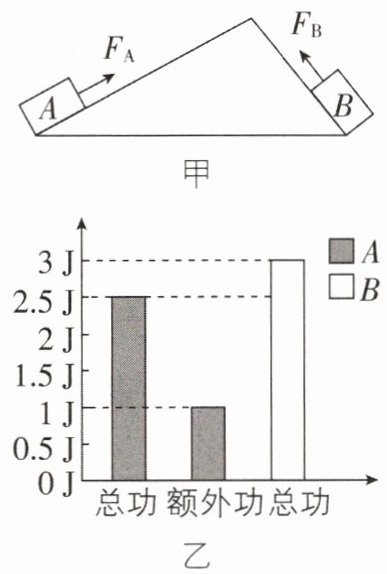
A.物体A的平均速度$v_{A}$小于物体B的平均速度$v_{B}$
B.小明对物体A做功的机械效率为40%
C.小明对物体A做的有用功$W_{A}$等于小芳对物体B做的有用功$W_{B}$
D.小明对物体A的拉力$F_{A}$小于小芳对物体B的拉力$F_{B}$
D
)
A.物体A的平均速度$v_{A}$小于物体B的平均速度$v_{B}$
B.小明对物体A做功的机械效率为40%
C.小明对物体A做的有用功$W_{A}$等于小芳对物体B做的有用功$W_{B}$
D.小明对物体A的拉力$F_{A}$小于小芳对物体B的拉力$F_{B}$
答案:
D 【解析】由图甲可知,相同时间内物体 A通过的路程大于物体 B 通过的路程,根据$v=\frac {s}{t}$可知,物体 A 的平均速度$v_{A}$大于物体 B 的平均速度$v_{B}$,故 A 不符合题意;由图乙可知,小明对物体 A 做的总功为 2.5 J,额外功为1 J,则$W_{有用}=W_{总}-W_{额外}=2.5J-1J=1.5J$,机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {1.5J}{2.5J}×100\% =60\% $,故 B 不符合题意;两物体体积相同,但不知道质量关系,不能得出重力关系,无法根据$W_{有用}=G_{物}h$判断有用功大小;由图乙可知对物体 A做的总功小于对物体 B 做 的总功,但不知道对物体 B 做的额外功的大小,故无法判断有用功 的大小,故 C 不符合题意;小明对物体 A做的总功小于小芳对物体 B 做 的总功,且物体 A 通过的路程大于物体 B 通过的路程,根据$W_{总}=Fs$可知,小明对物体 A 的拉力$F_{A}$小于小芳对物体 B 的拉力$F_{B}$,故 D符合题意。故选 D。
道路救援车拖移故障车辆时的情景可建构成如图所示的模型。钢绳对小车A施加沿斜面的拉力为$5×10^{3}N$,将重为$1×10^{4}N$的小车A从斜面底端匀速拉至斜面顶端。已知斜面高为1m,长为4m。在小车A从水平路面被拖上救援车的过程中(忽略小车的体积)(
A.该模型中的斜面和滑轮都可以省力
B.拉力做的功为$1×10^{4}J$
C.斜面的机械效率为75%
D.小车受到斜面的摩擦力为2500N
D
)A.该模型中的斜面和滑轮都可以省力
B.拉力做的功为$1×10^{4}J$
C.斜面的机械效率为75%
D.小车受到斜面的摩擦力为2500N
答案:
D【解析】该模型中的斜面可以省力,但定滑轮不省力,故 A不符合题意;拉力做的功$W_{总}=Fs=5×10^{3}N×4m=2×10^{4}J$,故 B 不符合题意;有用功$W_{有用}=Gh=1×10^{4}N×1m=1×10^{4}J$,则机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {1×10^{4}J}{2×10^{4}J}×100\% =50\% $,故 C 不符合题意;额外功$W_{额外}=W_{总}-W_{有用}=2×10^{4}J-1×10^{4}J=1×10^{4}J$,则小车受到斜面 的摩擦力$f=\frac {W_{额外}}{s}=\frac {1×10^{4}J}{4m}=2500N$,故D符合题意故选 D。
4滑轮组[2025江西九江期末,中]如图所示,定滑轮重2N,动滑轮重1N,物体A在拉力$F = 4N$的作用下,1s内沿竖直方向匀速升高了0.2m。不计绳重和摩擦,求:
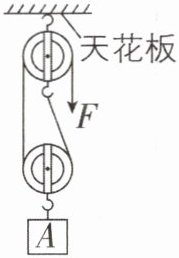
(1)滑轮组的机械效率;
(2)天花板对滑轮组的拉力;
(3)拉力做功的功率。

(1)滑轮组的机械效率;
(2)天花板对滑轮组的拉力;
(3)拉力做功的功率。
答案:
(1)由图知由两段绳子吊着动滑轮不计绳重和摩擦,物体 的重力$G=nF-G_{动}=2×4N^{-}1N=7N$,拉力做的有用功$W_{有用}=Gh=7N×0,2m=1,4J$,绳子自由端移动的距离$s=nh=2×0.2m=0.4m$,拉力做的总功$W_{总}=Fs=4N×0_{o}4m=1.6J$,滑轮组的机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {1.4J}{1.6J}×100\% =87.5\% $。
(2)天花板对滑轮组 的拉力$F_{拉}=G_{定}+3F=2N^{+}3×4N=14N$o
(3)拉力做功 的功率$P=\frac {W_{总}}{t}=\frac {L.6J}{1s}=L.6W$o
(1)由图知由两段绳子吊着动滑轮不计绳重和摩擦,物体 的重力$G=nF-G_{动}=2×4N^{-}1N=7N$,拉力做的有用功$W_{有用}=Gh=7N×0,2m=1,4J$,绳子自由端移动的距离$s=nh=2×0.2m=0.4m$,拉力做的总功$W_{总}=Fs=4N×0_{o}4m=1.6J$,滑轮组的机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {1.4J}{1.6J}×100\% =87.5\% $。
(2)天花板对滑轮组 的拉力$F_{拉}=G_{定}+3F=2N^{+}3×4N=14N$o
(3)拉力做功 的功率$P=\frac {W_{总}}{t}=\frac {L.6J}{1s}=L.6W$o
5核心素养科学思维甲、乙两机械的三种性能指标的对比如图所示(自中点O越向外,数值越大,例如$m_{甲}<m_{乙}$),与乙机械相比,甲机械(
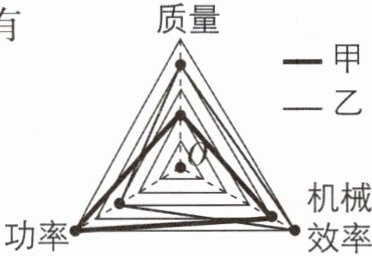
A.所消耗的能量更多(有用功相同时)
B.机械效率较高
C.做功较慢
D.有用功较小
A
)
A.所消耗的能量更多(有用功相同时)
B.机械效率较高
C.做功较慢
D.有用功较小
答案:
A【解析】由题图可知,甲、乙机械 的机械效率的大小关系为$η_{甲}<η_{乙}$,功率关系为$P_{甲}>P_{乙}$,故B,C错误机械效率悬有用功与总功 的比值,机械效率低有用功不一定小有用功相同时,机械效率越高,总功越小,故A正确,D错误
查看更多完整答案,请扫码查看


